 |
Кольцо многочленов над факториальным кольцом
|
|
|
|
Теорема 1. Группа обратимых элементов кольца A [ x ] совпадает с группой обратимых элементов кольца А.
Теорема 2. Если кольцо А факториально, то кольцо A [ x ] также факториально.
Примитивные многочлены. Содержание многочлена.
Лемма 1. Всякий многочлен f Î A [ x ] представляется в виде f = d j, где d Î A,
j – примитивный многочлен. Такое представление единственное, с точностью до ассоциированности над А.
Лемма 2. Всякий многочлен g Î Р [ x ], где Р – поле частных кольца А, представляется в виде f = 
j, где m, n Î A, j – примитивный многочлен.
Лемма 3. Всякий простой в A [ x ] многочлен является примитивным многочленом. Наоборот, всякий примитивный многочлен является либо простым многочленом, либо представляется в виде произведения примитивных многочленов меньшей степени.
Лемма 4. Лемма Гаусса. Произведение примитивных многочленов также является примитивным многочленом.
Лемма 5. Если два примитивных многочлена ассоциированы над полем частных факториального кольца, то они ассоциированы и над самим этим кольцом.
Лемма 6. Если многочлен f Î A [ x ] приводим над полем частных Р кольца А, то многочлен приводим и над А.
ГЛАВА 12. Кольцо многочленов от нескольких переменных
§ 1. Кольцо многочленов от n переменных
A [ x 1 x 2,..., xn –1, xn ] = A [ x 1 x 2,..., xn –1][ xn ].
Теорема 1. Наследование свойств кольца.
Если кольцо А коммутативно или ассоциативно, или содержит единицу, или является целостным кольцом, или факториальное кольцо, то этим же свойством обладает кольцо многочленов A [ x 1 x 2,..., xn –1, xn ].
Степень многочлена относительно переменной xi, cтепень многочлена относительно совокупности переменных. deg 
f, deg 
f. Однородные многочлены (формы) степени n.
|
|
|
Теорема 2. Свойства степени.
1°. deg (f ± g) £ max {deg f, deg g }; deg (f ± g) £ max {deg f, deg g }.
2°. deg (f × g) £ deg f + deg g; deg (f × g) £ deg f + deg g.
3°. Если кольцо А целостное, то
deg (f × g) = deg f + deg g; deg (f × g) = deg f + deg g.
Многочленная функция 
: Аn ® А, соответствующая многочлену f = f (x 1 x 2,..., xn).
Теорема 3. Свойства кольца многочленных функций.
1°. Множество 
всех многочленных функций является подкольцом в кольце всех функций, отображающих Аn в А.
2°. Соответствие F: f 
является эпиморфизмом кольца многочленов
А [ x 1 x 2,..., xn ] на кольцо многочленных функций .
3°. Если кольцо А бесконечное, то F является изоморфизмом.
§ 2. Лексикографическое (алфавитное) упорядочение многочлена от n переменных
Лексикографический порядок на множестве (неподобных) одночленов многочлена. ≻.
Теорема. Свойства лексикографического порядка ≻.
1°. Отношение ≻ транзитивно.
2°. Отношение ≻ линейно.
3°. Отношение ≻ стабильно относительно умножения на одночлен.
Следствие. Лемма о высшем члене произведения.
Высший член произведения многочленов равен произведению высших членов множителей.
Симметрические многочлены
Действие подстановки p на многочлен f. Симметрические многочлены. Элементарные симметрические многочлены. Степенные суммы.
Теорема 1. Множество SA [ x 1 x 2,..., xn ] симметрических многочленов от n переменных образует подкольцо в кольце A [ x 1 x 2,..., xn ] многочленов от n переменных.
Лемма 1. Если a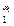x 
x 
... x 
– высший член симметрического многочлена в лексикографическом упорядочении, то последовательность его показателей степени составляет нестрого убывающую последовательность: a1 ³ a2 ³... ³ a n.
Лемма 2. Для любого одночлена a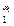x x ... x , показатели степени которого образуют нестрого убывающую последовательность: a1 ³ a2 ³... ³ a n, существует, и, причём только один, одночлен от элементарных симметрических многочленов a s 
s 
... s 
, старший член которого совпадает с этим одночленом.
|
|
|
Теорема 2. Основная теорема теории симметрических многочленов.
Всякий симметрический многочлен может быть представлен в виде многочлена от элементарных симметрических многочленов.
Теорема 3. Всякий симметрический многочлен единственным образом представляется в виде многочлена от элементарных симметрических многочленов.
Метод неопределённых коэффициентов для выражения однородного симметрического многочлена через элементарные симметрические многочлены.
Связь с формулами Виета.
Решение симметрических систем уравнений.
|
|
|
