 |
Гомоморфизмы и эпиморфизмы групп. Теорема об эпиморфизмах
|
|
|
|
Определение, примеры и простейшие свойства гомоморфизма групп. Ядро гомоморфизма. Ker f.
Теорема 1. Критерий нормальной подгруппы.
Подгруппа H группы G является нормальной подгруппой тогда и только тогда, когда существует гомоморфизм группы G, ядром которого является H.
Теорема 2. Если f: G ® G 1 – гомоморфизм групп и H = Ker f – ядро гомоморфизма, то для любого a 1Î G 1 его полный прообраз f –1(a 1) является либо пустым множеством, либо представляет собой смежный класс группы G по подгруппе H.
Теорема 3. Теорема об эпиморфизмах.
Если f: G ® G 1 – эпимоморфизм групп, H = Ker f, j: G ® G / H – естественный эпиморфизм, то существует, и причём единственный, изоморфизм q: G / H ® G 1, обладающий свойством f = q°j.
ГЛАВА 16. Кольца и поля
Кольца и поля
Примеры колец: Z, Q, R [ x ],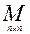 
, á R 3; +, ´ñ. Особенности этих примеров.
Нулевой и единичный элементы, противоположный и обратный элементы.
Теорема 1. Свойства противоположных и обратных.
1°. В кольценуль и единица единственные.
2°. В кольце каждый элемент имеет единственный противоположный;
в поле каждый ненулевой элемент имеет единственный обратный.
3°. В кольце: –0 = 0; в поле: 1–1 = 1.
4°. –(a + b) = (– a)+(– b); (ab)–1 = a –1 b –1.
5°.–(– a) = a; (a –1)–1 = a.
Теорема 2. О расщеплении.
1°. В кольце(" a)(" b)($! c)(b + c = a).
2°. В поле (" a)(" b ¹0)($! c)(b × c = a).
Разность и частное: a – b, 
.
Теорема 3. Свойства разности.
1°. (a – b)+ b = a.
2°. a – b = a+ (– b).
3°. 0– a = – a.
4°. a +(b – c) = (a + b)– c.
5°. a – b = c – d «a + d = b + c.
6°. a – b = a «b = 0.
7°. a – b = 0 «a = b.
8°. a –(– b) = a + b.
9°. a –(b + c) = (a – b)– c.
10°. a –(b – c) = (a – b)+ c.
11°. (a – b)+(c – d) = (a+c)–(b+d).
12°.(a – b)–(c – d) = (a+d)–(b+c).
13°. (a – b)×(c – d) = (ac+bd)–(bc+ad).
|
|
|
Теорема 4. Законы сокращения.
1°. В кольце a + b = a + c ® b = c.
2°. В поле a × b = a × c ® a = 0 Ú b = c.
Теорема 5. Следствия аксиомы дистрибутивности.
1°. a ×0 = 0× a = 0.
2°. (a – b) c = ac – bc.
3°. (– a) b = a (– b) = – ab.
4°. (– a)(– b) = ab.
5°. a – b = c – d «a + d = b + c.
6°. a – b = a «b = 0.
Теорема 6. Условия обратимости и равенства нулю в поле.
1°. a × b = 0 «a = 0 Ú b = 0.
2°. = 0 «a = 0 Ù b ¹ 0.
3°. 0 не обратим; a обратим «a ¹ 0.
4°. Если a обратим, то – a тоже обратим, причем (– a)–1 = – a –1.
Теорема 7. Свойства частного в поле.
Пусть b ¹ 0 и d ¹ 0. Тогда
1°. × b = a.
2°. = a × b –1.
3°. 
= b –1.
4°. a × 
= 
.
5°. = 
«ad = bc Ù b ¹ 0 Ù d ¹ 0.
6°. = a «b = 1 Ú a = 0.
7°. = 1 «a = b Ù b ¹ 0.
8°. 
= a × b.
9°. 
= 
.
10°. 
= .
11°. 
= : d.
12°. a: 
= 
.
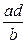13°. + = 
.
14°. – = 
.
15°. × = 
.
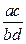16°. Если с¹ 0, то : = 
.
Изоморфизм колец и полей. Отношение изоморфизма @.
Теорема 8. Свойства изоморфизма колец и полей.
1°. Тождественное отображение является изоморфизмом.
2°. Отображение, обратное изоморфизму, является изоморфизмом.
3°. Композиция двух изоморфизмов является изоморфизмом.
4°. Отношение изоморфизма является отношением эквивалентности.
Гомоморфизмы и эпиморфизмы колец. Примеры. Простейшие свойства гомоморфизмов.
Теорема 9. Некоторые конструкции.
1°. Прямое (декартово) произведение колец также является кольцом.
2°. Эпиморфный образ кольца также является кольцом.
3°. Алгебра, изоморфная кольцу (полю), сама является кольцом (полем).
Подкольца и подполя
Определение и примеры подколец и подполей.
Теорема 1. Первый критерий подкольца.
Пусть á A; +, ×ñ – кольцо, B Ì A. Тогда B является подкольцом кольца A, если и только если одновременно выполняются следующие четыре условия:
1) B ¹ Æ; 2) a 1, a 2Î B Þ a 1 +a 2 Î B; 3) a Î B Þ – a Î B; 4) a 1, a 2Î B Þ a 1 a 2 Î B.
Теорема 2. Второй критерий подкольца.
|
|
|
Пусть á A; +, ×ñ – кольцо, B Ì A. Тогда B является подкольцом кольца A, если и только если одновременно выполняются следующие три условия:
1) B ¹ Æ; 2) a 1, a 2Î B Þ a 1– a 2 Î B; 3) a 1, a 2Î B Þ a 1 a 2 Î B.
Теорема 3. Критерий подполя.
Пусть á A; +, ×ñ – поле, B Ì A. Тогда B является подполем поля A, если и только если одновременно выполняются следующие три условия:
1) B * ¹ Æ; 2) a 1, a 2Î B Þ a 1– a 2 Î B; 3) a 1, a 2Î B * Þ a 1 a 2–1 Î B *.
Теорема 4. Особенности числовых подколец и подполей.
1°. Кольцо целых чисел является наименьшим числовым кольцом с единицей.
2°. Поле рациональных чисел является наименьшим числовым полем.
3°. Всякий изоморфизм числовых полей действует тождественно на множестве рациональных чисел.
|
|
|
