Целые степени элемента группы. Порядок элемента группы. Циклические группы

 

Определение целой степени элемента группы.

 

Теорема 1. Свойства целой степени элемента группы.

1°. (a ^–1) ⁿ = (aⁿ)^–1 для любого n Î N.

2°. a^maⁿ = a^{m + n} для любых m, n Î Z.

3°. (a^m) ⁿ = a^{m × n} для любых m, n Î Z.

 

Порядок элемента группы. оrd a.

 

Теорема 2. Свойства порядка.

 

Пусть ord a = n. Тогда

1°. Элементы a ⁰ = e, a, a ²,..., a^{n –1} различны и любая целая степень элемента a совпадает с одним из этих элементов.

2°. a^k = a^l тогда и только тогда, когда k – l n.

3°. a^k = e тогда и только тогда, когда k n.

4°. При 0 £ k, l < n a^k × a^l =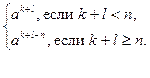

 

Определение циклической группы. á а ñ.

Примеры циклических групп: á Z; +ñ, á ; ×ñ.

 

Теорема 3. Изоморфизм циклических групп.

 

1°. Любые две циклические группы порядка n изоморфны.

2°. Любые две циклические группы бесконечного порядка изоморфны.

 

Подгруппы

 

Определение и примеры подгрупп.

 

Теорема 1. Первый критерий подгруппы.

 

Пусть á G; ×ñ – группа, H Ì G. Тогда H является подгруппой группы H, если и только если одновременно выполняются следующие три условия:

1) H ¹ Æ; 2) h ₁, h ₂Î H Þ h ₁ h ₂ Î H; 3) h Î H Þ h ^–1Î H.

 

Теорема 2. Второй критерий подгруппы.

 

Пусть á G; ×ñ – группа, H Ì G. Тогда H является подгруппой группы H, если и только если одновременно выполняются следующие два условия:

1) H ¹ Æ; 2) h ₁, h ₂Î H Þ h ₁ h ₂^–1 Î H.

 

Теорема 3. О подгруппах циклической группы.

 

Любая подгруппа циклической группы также является циклической группой.

 

Пересечение и объединение групп. Объединение возрастающей цепочки подгрупп.

 

Теорема Кэли

 

Теорема. Любая группа G изоморфна некоторой подгруппе группе биекций некоторого множества. В частности, любая конечная группа порядка n изоморфна некоторой подгруппе группы S_n.

 

Этапы доказательства

1. l _a: x ax – биекция G в G. 2. = {l _a: a Î G } – подгруппа в P (G).

3. F: a l _a – изоморфизм G на .

 

Разбиение группы по подгруппе. Теорема Лагранжа

 

Умножение подмножеств группы. H ₁ H ₂. Ha. aH.

 

Теорема 1. Свойства умножения подмножеств.

 

1°. Умножение подмножеств ассоциативно.

2°. Если H – подгруппа группы G, то Ha = H тогда и только тогда, когда a Î H.

3°. Если H – подгруппа группы G, то отображение r _а: H ® Ha по правилу

h ha является биекцией. В частности, если H – конечная подгруппа, то = .

 

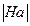Отношение r _H правой смежности: a r _Hb Û Ha = Hb.

 

Теорема 2. Свойства отношения правой смежности.

 

1°. Отношение r _H является отношением эквивалентности.

2°. Если K_a – класс эквивалентности, порождённый элементом a, то K_a = Ha.

 

Теорема 3. Теорема Лагранжа.

Порядок конечной группы делится на порядок любой её подгруппы.

 

Теорема 4. Если G – конечная циклическая группа порядка n и d произвольный делитель числа n, то существует подгруппа H группы G порядка d.

 

Нормальные подгруппы. Фактор-группы. Естественный эпиморфизм

Примеры и контрпримеры нормальных подгрупп.

 

Теорема 1. Критерий нормальной подгруппы.

 

Подгруппа H группы G является нормальной подгруппой тогда и только тогда, когда выполняется условие: x Î G Ù h Î H Þ x ^–1 hx Î H.

 

Теорема-определение 2. Множество правых (= левых) смежных классов группы G по нормальной подгруппе H является группой относительно операции _°, определённой правилом Ha _° Hb = Hab. Эта группа называется фактор-группой группы G по нормальной подгруппе H: á G / H; _°ñ.

 

Теорема-определение 3. Отображение j: a Ha группы G на фактор-группу G / H является эпиморфизмом. Этот эпиморфизм называется естественным эпиморфизмом группы G на фактор-группу G / H.

 

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: