ГЛАВА 13. Многочлены над основными числовыми полями

 

Кольцо многочленов над полем комплексных чисел

 

 

Теорема. Основная Теорема Алгебры.

Всякий многочлен ненулевой степени с комплексными коэффициентами имеет хотя бы один комплексный корень.

 

Следствие 1. Число корней многочлена с комплексными коэффициентами равна степени этого многочлена, если каждый корень считать столько раз, какова его кратность.

 

Следствие 2. Над полем комплексных чисел неприводимы только многочлены первой степени. Каноническое разложение многочлена над С имеет вид

a_n (x –a₁) (x –a₂) ... (x –a _s) .

 

Следствие 3. Над С f g Û все корни g являются корнями f, при этом их кратности для g не превосходят кратностей для f.

 

§ 2. Кольцо многочленов над полем действительных чисел

Теорема 1. Если комплексное число a является корнем многочлена с действительными коэффициентами, то комплексно сопряжённое число также является корнем этого многочлена. При этом кратности a и совпадают.

 

Теорема 2. Над полем действительных чисел неприводимы только многочлены первой степени и многочлены второй степени с отрицательным дискриминантом. Каноническое разложение многочлена над R имеет вид

a_n (x –a₁) (x –a₂) ... (x –a _s) (x ²+ p ₁ x + q ₁) )(x ²+ p ₂ x + q ₂) ... (x ²+ p_tx + q_t) ,

где p для i = .

 

Многочлены над полем рациональных чисел

 

Сведение вопросов отыскания рациональных корней и разложения на множители многочленов над Q к многочленам над Z.

 

Теорема 1. Если f (x) = a_nxⁿ + a_{n –1} x ^{n –1}+... + a ₁ x + a ₀Î Z [ x ] и рациональное число a = 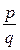, где p и q – взаимно простые числа, является корнем f, то a ₀ p, a_n q.

 

Теорема 2. Если f (x) Î Z [ x ] и рациональное число a = 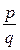, где p и q – взаимно простые числа, является корнем f, то (" m Î Z)().

Теорема 3. Критерий неприводимости Эйзенштейна.

 

Если f (x) = a_nxⁿ + a_{n –1} x ^{n –1}+... + a ₁ x + a ₀Î Z [ x ] и существует такое простое число p, что a_n не делится на p, все остальные коэффициенты делятся на p и a ₀ не делится на p ², то многочлен f неприводим над Z, а, следовательно, и над Q.

 

 

ГЛАВА 14. Расширения числовых полей. Алгебраические числа

 

§ 1. Простое расширение Р (a) поля Р

 

Теорема 1. Строение Р (a).

 

Всякий элемент простого расширения поля Р с помощью элемента a представляется в виде отношения значений от a многочленных функций над Р:

Р (a) = {b: ($ )($ )(b = Ù Ù )}.

 

Алгебраические и трансцендентные над полем Р элементы.

 

Теорема 2. Строение простого трансцендентного расширения.

 

Если a – трансцендентный над полем Р элемент, то каждый элемент из Р (a) единственным образом представляется в виде b = , где f и g – взаимно простые многочлены и g – нормированный многочлен.

 

Примитивный многочлен алгебраического элемента.

 

Теорема 3. Строение простого алгебраического расширения.

 

Пусть a – алгебраический над полем Р элемент. Тогда

1°. Минимальный многочлен j элемента a неприводим над Р.

2°. Если deg j = n, то всякий элемент bÎ Р (a) представляется в виде

b = , где f Î Р [ x ] и deg f < n.

3°. Представление 2° единственно.

 

Освобождение от алгебраической иррациональности в знаменателе дроби.

 

Последовательное (цепное) расширение поля. Расширение поля конечной совокупностью элементов

 

Р (a₁)(a₂)... (a _n). P (a₁, a₂,..., a _n).

 

Теорема 1. Р (a₁)(a₂)... (a _n) = P (a₁, a₂,..., a _n).

Теорема 2. Строение P (a₁, a₂,..., a _n). Всякий элемент расширения поля Р с помощью элементов a₁, a₂,..., a _n представляется в виде отношения значений от a₁, a₂,..., a _n многочленных функций над Р: P (a₁, a₂,..., a _n) =

= .

 

Конечное расширение поля

 

Расширение поля как векторное пространство над этим полем. .

 

Теорема 1. Критерий конечности простого расширения.

 

Поле Р (a) является конечным расширением тогда и только тогда, когда элемент a является алгебраическим над полем Р.

 

Теорема 2. Свойства конечных расширений.

 

1°. Если кольцо А, являющееся расширением поля Р, является конечномерным векторным пространством над Р, то всякий элемент из А является алгебраическим над полем Р.

2°. Всякое кольцо, являющееся конечномерным векторным пространством над полем Р, является полем.

3°. Транзитивность конечного расширения. Если К – конечное расширение поля Р, а L – конечное расширение поля К, то L является конечным расширением поля Р, причём выполняется равенство = × .

 

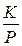§ 4. Алгебраические над полем Р элементы

 

Теорема 1. Множество алгебраических над полем Р элементов является полем.

 

Теорема 2. Поле алгебраических над полем Р элементов алгебраически замкнуто.

 

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: