 |
Существование поля частных целостного кольца
|
|
|
|
Теорема. Любое целостное кольцо имеет поле частных.
Этапы построения поля частных.
1. Алгебра пар á А ´ А *; +, ×ñ: коммутативность и ассоциативность операций; не дистрибутивность; наличие нейтральных элементов; необратимость каждой из операций.
2. Отношение сравнения ~ между парами: ~ – отношение эквивалентности, стабильное относительно операций.
3. Фактор-кольцо á А ´ А */~; Å, Äñ: фактор-кольцо является полем.
4. Подкольцо фактор-кольца 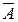 = {
= {  : a Î A }:
: a Î A }: 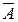 @ A.
@ A.
5. Фактор-кольцо á А ´ А */~; Å, Äñ является полем частных кольца 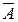 .
.
Приложение 2
1°. Использование теоремы о числе корней ненулевого многочлена
1. Доказать тождество:
а) (x – y)(xz +1)(yz +1)+(y – z)(yx +1)(zx +1)+(z – x)(zy +1)(xy +1) = (x – y)(y – z)(z – x);
б) 
2. Разложить на множители выражение:
а) a 3(b – c)(c – d)(d – b)– b 3(c – d)(d – a)(a – c)+ c 3(d – a)(a – b)(b – d)– d 3(a – b)(b – c)(c – a);
б) (a – b)3+(b – c)3+(c – a)3;
в) 4(a 2 c + c 2 b + b 2 a)–2(a 2 b + b 2 c + c 2 a)–7 abc;
г) (a + b + c)(ab + bc + ca)– abc;
д) ab (a – b)– ac (a + c)+ bc (2 a – b + c);
е) a 2(b – c)+ b 2(c – a)+ c 2(a – b);
ж) a 3(b – c)+ b 3(c – a)+ c 3(a – b);
з) ab (a 2– b 2)+ bc (b 2– c 2)+ ca (c 2– a 2).
3. Доказать, что функция sin не является многочленом.
4. Пусть a, b, c –различные числа. Легко проверить, что эти числа являются корнями многочлена 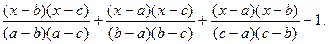
Нет ли здесь противоречия с теоремой о числе корней многочлена?
2°. Доказательство неравенств
А. Выделение полного квадрата
1. Доказать, что для любых чисел a, b, c справедливо неравенство a 2 +b 2 +c 2 ab+bc+ca, причем равенство выполняется, если только a = b = c.
2. Доказать, что для любых a справедливо неравенство a 4 –a+ 0,5 > 0.
3. Известно, что уравнение x 4 +ax 3 + 2 x 2 +bx+ 1 = 0 имеет хотя бы один корень. Доказать, что справедливо неравенство a 2 +b 2 8.
4. a 2+ b 2–2 ab+ 2 a– 2 b+ 10.
|
|
|
5. a 2+4 b 2 + 4 b– 4 a+ 50.
Б. Использование свойств квадратичной функции
1. Доказать, что при всех a 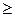 0справедливо неравенство 10 a 3 – 9 a 2 + 9 a+
0справедливо неравенство 10 a 3 – 9 a 2 + 9 a+ 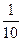 > 0.
> 0.
2. Доказать, что при любых значениях a и b имеет место неравенство a 2 + 2 ab+ 3 b 2 + 2 a+ 6 b+ 4 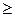 1.
1.
3. Доказать, что если (a + c)(a + b + c) < 0и a 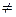 0, тосправедливо неравенство
0, тосправедливо неравенство
(b – c)2 > 4 a (a + b + c).
4. Про положительные числа a 1, b 1, c 1, a 2, b 2, c 2известно, что b 12  a 1 c 1, b 22
a 1 c 1, b 22 
£ a 2 c 2. Доказать, что (a 1+ a 2+5)(c 1 +c 2+2) > (b 1+ b 2 + 3)2.
5. Доказать, что при любых значениях а справедливо неравенство (a 3 –a+ 2)2 > > 4 a 2(a 2 + 1)(a –2).
6. Доказать, что если ненулевые действительные числа a, b, c удовлетворяют равенствам a + b + c = abc, a 2 = bc, то a 2 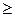 3.
3.
7. Уравнение ax 2 +bx+c = 0 не имеет действительных корней, a + b + c < 0. Какой знак имеет число c?
8. Доказать, что если a, b и c –стороны треугольника, то уравнение
b 2 x 2 + (b 2 +c 2 –a 2) x + c 2 = 0 не имеет действительных корней.
9. Доказать, что выражение 3  неотрицательно при любых ненулевых x и y.
неотрицательно при любых ненулевых x и y.
10. Доказать, что если числа a, b, c удовлетворяют условиям a + b + c = 5, ab+bc+ca = 8, то 1  a
a 
 , 1
, 1  b
b 
 , 1
, 1  c
c 
 .
.
11. Доказать, что если a + b + c > 0, ab+bc+ca > 0, abc > 0, то числа a, b, c положительные.
3°. Дискретность порядка на множестве натуральных и целых чисел
1. Доказать, что не существует строго возрастающей последовательности (an) целых неотрицательных чисел, для которой при любых m и n выполняется соотношение amn = am+an.
2. Решить в Z систему x + y 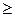 25, y
25, y  2 x +18, y
2 x +18, y 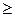 x 2 + 4 x.
x 2 + 4 x.
3. Доказать, что при любом натуральном n число n 4 + 2 n 3 + 2 n 2 + 2 n+ 1 не является полным квадратом.
4. При каких значениях n Î N выражение n 3+7 n 2+6 n +1 является кубом натурального числа?
5. Сколько пар целых чисел (x; y) удовлетворяет системе неравенств
2 x 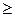 3 y, 3 x
3 y, 3 x 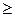 4 y, 5 x –7 y
4 y, 5 x –7 y  20?
20?
6. Найти целую часть выражения  .
.
7. Могут ли числа a 2 +b и b 2 +a, где a, b Î N,одновременно быть полными квадратами?
8. Найти все пары натуральных чисел a и b, для которых числа a 2+3 b и 3 a + b 2одновременно являются квадратами натуральных чисел.
9. Какое число стоит в последовательности 1, 2, 2, 3, 3, 3, 4, 4, 4, 4,... на 500000-м месте?
|
|
|
10. К десятичной записи числа 2 k приписали десятичную запись числа 5 k. Сколько десятичных знаков содержит получившееся число?
11. Какое наименьшее неотрицательное число можно получить из чисел
1, 2,..., 1997 путем расстановки перед ними знаков “+” и “–” и последующего выполнения указанных действий?
12. Какое наименьшее неотрицательное число можно получить из чисел
12, 22,..., 19972 путем расстановки перед ними знаков “+” и “–” и последующего выполнения действий?
Оценка с помощью неравенств + перебор
13. Решить в Z уравнение x 2+ y 2 = x + y +2.
14. Решить в Z уравнение x 6 + 3 x 3 + 1 = y 4.
15. Решить в Z уравнение (x +2)4 –x 4 = y 3.
16. Решить в Z уравнение x 2 +xy+y 2 = x 2 y 2.
17. Решить в Z уравнение x 2+ x = y 4+ y 3+ y 2+ y.
|
|
|


