24.Основные понятия булевой алгебры: булев куб, булевы функции.

24. Основные понятия булевой алгебры: булев куб, булевы функции.

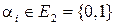Набор , где , , называется булевым (двоичным) вектором, а – его компонентами (координатами). Для двух векторов  и 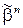 полагаем 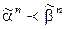, если  для всех .

Число 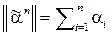 называется весом (нормой) набора , а n называется его длиной. Каждому  сопоставляется его номер 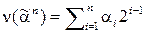. Несложно показать, что общее число двоичных наборов длины n равно .

Частично упорядоченное множество  всех наборов  называется n-мерным булевым (двоичным) кубом, а 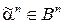 называется вершиной куба. Вершины, имеющие одинаковый вес k, образуют k-й слой  булева куба.

Число  называется расстоянием Хэмминга между вершинами  и равно числу координат, в которых наборы  и 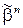 отличны друг от друга. Оно также равно минимальному числу ребер булева куба, по которым нужно пройти, чтобы дойти от вершины  до .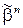

Если , то вершины  и 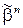 называются соседними, а если для таких вершин 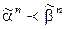, то вершина  непосредственно предшествует 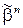. Если , то вершины  и 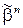 называются противоположными.

Функция  называется функцией алгебры логики или булевой функцией. Множество всех булевых функций, зависящих от переменных 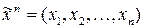, обозначается через 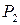, причем .

Элементарные булевы функции одной переменной определяет

Таблица 1 Элементарные булевы функции одной переменной

x			x

 

 

Таблица 2 Элементарные булевы функции двух переменных

		&					|

 

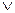
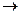
 называется импликацией(читается " из  следует " )

 называется штрихом Шеффера (читается " не  или не " )

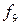 называется стрелкой Пирса (читается " не  и не " )

25. Элементарные булевы функции, их свойства. Существенные и фиктивные переменные. Основные функциональные элементы.

Таблица 1 Элементарные булевы функции одной переменной

x			x

 

 

Таблица 2 Элементарные булевы функции двух переменных

		&					|

 

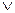
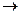
 называется импликацией(читается " из  следует " )

 называется штрихом Шеффера (читается " не  или не " )

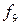 называется стрелкой Пирса (читается " не  и не " )

Переменная 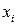 (i-я координата набора ) булевой функции  называется существенной, если можно указать такие два соседних по i-й координате двоичных набора, что значения функции на этих наборах различны. В противном случае, переменная 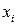 называется фиктивной (несущественной). Две булевы функции называются равными, если одну из них можно получить из другой добавлением или удалением фиктивных переменных. Пусть булевы функции f₁(х₁, х₁) и f₂(х₁, х₂) заданы следующей таблицей истинности:

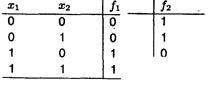
Для этих функций переменная х₁ — существенная, а переменная х₂ несущественная.

 

Техническая реализация элементарных функций основана на применении различных физических явлений. Для реализации функций алгебры логики используются базисные функциональные элементы, изображаемые в виде прямоугольников, причем инверсные входы и выход изображают пустыми кружками. В верхней части прямоугольника ставится знак, указывающий операцию: & – конъюнкция, 1 – дизъюнкция, M2 – сложение по 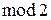, 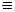– эквивалентность.

Например, на рисунке 2 показан функциональный элемент Шеффера

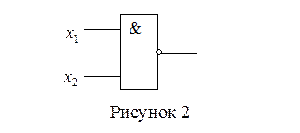
Более сложные элементы графически изображаются в виде композиции базисных функциональных элементов.

26. Формулы. Реализация булевых функций формулами. Принцип двойственности.

Как и в обычной алгебре на базе элементарных функций строятся формулы, которые можно определить индуктивно. Пусть 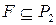– некоторое подмножество булевых функций. Тогда

a) каждая  называется формулой над F;

b) если  и – формулы над F или символы булевых переменных, то выражение  называется формулой над F.

Выражение в пункте b) можно найти с использованием двух простых операций: подстановки переменных, включающей в себя их переименование, перестановку и отождествление; бесповторной подстановки функций, позволяющей строить выражения , где 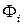– либо формула, либо булева переменная, причем хотя бы одна  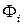отлична от переменной, а множества переменных, входящих в формулы  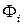и 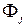, не пересекаются.

При построении формул применяются переменные, множество связок  и скобки, причем при опускании некоторых из них связка  считается самой сильной, а связка – сильнее любой другой двухместной связки. Каждая формула над F может быть получена из функций, принадлежащих F, применением сначала операции бесповторной подстановки функций (многократной), а затем однократной операции подстановки переменных.

Запись  означает, что  построена на функциях , а запись  указывает на переменные, используемые при построени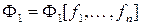и .  и  имеют одинаковое строение , если  получена из 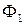 путем замены .

Формуле  над F по индукции сопоставим булеву функцию :

a) если , то формуле  соответствует ;

b) если , где – формулы над F или символы переменных, то формуле  отвечает функция , где  при  либо тождественная функция (переменная), либо .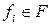

Формула  реализует f и любую равную ей функцию, если f соответствует . Функция f, соответствующая формуле , называется суперпозицией функций из F. Строение формулы можно описать помеченным деревом. Так, формуле  соответствует дерево рисунка 1

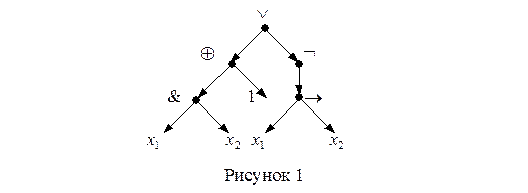
Функция 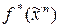 называется двойственной к функции , если имеет место равенство 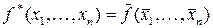. Класс S самодвойственных функций образуют функции, для которых .

 

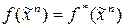Справедлив следующий принцип двойственности: если функция f реализуется формулой 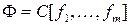, то двойственная ей функция  реализуется формулой 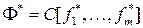, имеющей такое же строение, как и формула . С помощью этого принципа легко строится формула, реализующая функцию, двойственную к заданной функции.

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: