27.Разложение булевых функций по переменным. Совершенная ДНФ и совершенная КНФ.

27. Разложение булевых функций по переменным. Совершенная ДНФ и совершенная КНФ.

 

Для булевой переменной x и параметра s выражение

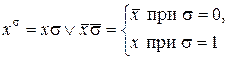
принимает значение 1 тогда и только тогда, когда .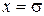

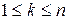Каждую функцию алгебры логики  при  можно представить в следующей форме:

,

где дизъюнкция берется по всем наборам переменных .

В частности при 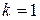 имеем разложение по переменной :

,

а при 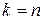 получаем представление:

,

называемое совершенной ДНФ (ДНФ – дизъюнктивная нормальная форма).

Таким образом, имеет место

Теорема 1. Каждая булева функция может быть представлена в виде формулы через отрицание, дизъюнкцию и конъюнкцию.

С помощью принципа двойственности находится представление:

,

называемое совершенной КНФ (КНФ – конъюнктивная нормальная форма).

 

Формулы  и  называются соответственно ДНФ и КНФ, если элементарные конъюнкции (дизъюнкции) в них попарно различны, а число l элементарных конъюнкций (дизъюнкций) называется их длиной.

28. Полиномы Жегалкина. Не полностью определенные (частичные) булевы функции.

Каждая булева функция единственным образом представима в виде полинома по 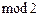 ( полинома Жегалкина ):

,

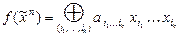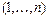где суммирование проводится по всем подмножествам  множества из n чисел , а коэффициенты полинома принимают значения из . В частности, полином Жегалкина функции 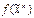 можно найти, применяя метод неопределенных коэффициентов.

Булеву функцию n переменных называют неполностью определенной или частичной, если она определена не на всех двоичных наборах длины n. Неполностью определенная булева функция не попадает под определение булевой функции, но при произвольном доопределении (на всех наборах, на которых она не определена) это несоответствие снимается. Легко убедиться, что если булева функция f не определена на m наборах аргументов, то путем ее доопределения можно получить 2^m различных полностью определенных функций. Существует не более чем 2²ⁿ различных булевых функций n переменных. К этому выводу легко прийти, пользуясь простыми комбинаторными рассуждениями, и вспомнив, что на каждом из 2ⁿ наборов функции могут принимать два значения.

29. Виды ДНФ и КНФ: сокращенные, минимальные, кратчайшие, тупико-вые.

,

совершенная ДНФ (ДНФ – дизъюнктивная нормальная форма).

 

,

совершенная КНФ (КНФ – конъюнктивная нормальная форма).

Формулы  и 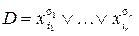 называются соответственно элементарными конъюнкцией и дизъюнкцией, если каждая переменная входит в них не более одного раза, а число r букв вида  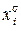называется их рангом.

Формулы  и  называются соответственно ДНФ и КНФ, если элементарные конъюнкции (дизъюнкции) в них попарно различны, а число l элементарных конъюнкций (дизъюнкций) называется их длиной. Сумма рангов всех конъюнкций (дизъюнкций), входящих в ДНФ (КНФ), называется сложностью ДНФ (КНФ). Совершенная ДНФ (КНФ) функции  составлена из элементарных конъюнкций (дизъюнкций) ранга n.

Импликантой функции  называется элементарная конъюнкция K, обладающая свойством: . Она называется простой, если после удаления из нее любой буквы вида 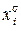 получается конъюнкция, не являющаяся импликантой функции . Дизъюнкция всех простых импликант функции  называется сокращенной ДНФ функции .

ДНФ называется минимальной, если она содержит наименьшее число букв среди всех ДНФ, эквивалентных ей.

ДНФ называется кратчайшей, если она имеет наименьшую длину среди всех ДНФ, эквивалентных ей.

ДНФ называется тупиковой, если удаление из нее любой элементарной конъюнкции или буквы приводит к ДНФ, не эквивалентной исходной ДНФ.

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: