2. Равновесная термодинамика. 3. Отклонения от равновесия – термодинамический подход

2. РАВНОВЕСНАЯ ТЕРМОДИНАМИКА

 

       Не вдаваясь в детали классического термодинамического описания, которое подробно приводится в курсе физической химии, напомним лишь несколько основных положений, касающихся законов, управляющих поведением термодинамических систем.

       Равновесные (обратимые) процессы, протекающие бесконечно медленно, исключают из рассмотрения время, затрачиваемое на такие процессы, то есть времени в равновесной термодинамике нет. Рассмотрение равновесных процессов необходимо, поскольку при этих процессах многие важные величины, поддающиеся расчёту (в частности, работа тепловых машин), имеют максимальные значения. При этом в качестве первого принципа (первого постулата, первого начала) вводится закон сохранения энергии, который имеет вид статического баланса энергии в отсутствие потоков и позволяет количественно определить энергетику происходящих процессов, не указывая их направления.

       Для описания неравновесных (необратимых) процессов вводится ключевое для всего здания современной науки понятие – энтропия. Постулируется, во-первых, что энтропия является функцией состояния S = S(p, T) и, во-вторых, энтропия - величина аддитивная, т. е. энтропия системы складывается из энтропий составляющих её элементов. Второе начало (второй принцип) термодинамики постулирует, что для изолированной (в том числе адиабатно изолированной) равновесной системы всегда реализуется только состояние с S=S_max, т. е. в этом состоянии dS=0. Если систему вывести из состояния равновесия, то критерием поведения будет стремление энтропии к максимуму S→ S_max, dS→ 0, т. е. система стремится к равновесному состоянию, которое является конечным, устойчивым состоянием.

       Для описания процессов в открытых системах, происходящих в различных условиях, вводятся термодинамические потенциалы (энергия Гиббса G, энергия Гельмгольца A и др. ), включающие энтропийный вклад Q=TS, причём критерием протекания необратимых процессов является стремление к минимуму соответствующего процессу термодинамического потенциала - здесь удобно провести аналогию с равновесием в механической системе, которая во внешнем поле стремится к минимуму механического потенциала (система шарик на склоне ямки в поле тяжести, который всегда скатывается на дно).

Первый промежуточный итог:

Механика – позволяет анализировать простые системы:

- для консервативных систем – интервалы времени можно рассчитывать, но время обратимо, поэтому направление процессов определить нельзя, если не заданы начальные условия;

- для диссипативных систем – существует конечное состояние, а следовательно, и направление процесса; время достижения конечного состояния (состояния механического равновесия) можно определить, если известна скорость диссипации энергии.

Равновесная термодинамика – позволяет анализировать сложные системы:

- для термодинамических систем - если процессы обратимы (квазистатические, то есть бесконечно медленные), то можно определять изменения термодинамических параметров, т. е. проводить описание заданного процесса;

- если процессы необратимы – существует конечное состояние процесса (термодинамическое равновесие), и можно определять по исходным данным его параметры и направление процесса, однако время достижения конечного состояния не определяется.

        

3. ОТКЛОНЕНИЯ ОТ РАВНОВЕСИЯ – ТЕРМОДИНАМИЧЕСКИЙ ПОДХОД

 

Как анализировать неравновесные сложные системы, можно ли использовать для этого термодинамический способ описания? Рассмотрим некоторую произвольную сложную систему, которая находится в состоянии термодинамического равновесия. Любые изменения в системе, в том числе эволюция, приводящая к появлению упорядоченных структур, могут происходить только при условии, что она находится в неравновесном состоянии, так как состояние равновесия является устойчивым и конечным в ряду последовательных состояний системы. Поэтому выведем систему из состояния равновесия и проследим за её дальнейшим поведением (эволюцией), которое, что вполне естественно, будет зависеть от величины отклонения. При описании системы с помощью совокупности произвольных макроскопических параметров a_i её состояние с разной степенью отклонения от положения равновесия δ a_i  можно представить с помощью схемы, которая носит название диаграммы Бокштейна, по имени её автора - диаграмма Бокштейна представлена на рис. 3. 1:

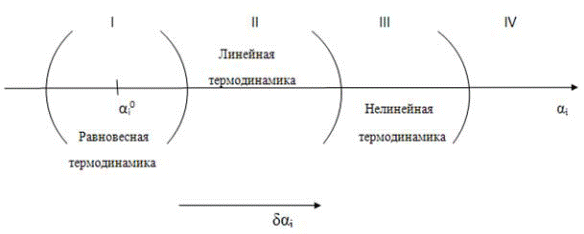
Рис. 3. 1. Диаграмма Бокштейна: термодинамические способы описания систем в зависимости от степени отклонения от равновесного состояния.

Степень отклонения от равновесия откладывается на диаграмме по горизонтальной оси, начало отсчета δ a_i=0. Введём в качестве величины, которая характеризует состояние системы, параметр A (это может быть температура, концентрация какого-либо компонента, фазовый состав и др. ), который зависит от совокупности параметров a_i :

A = A(a_i)                                                         (3. 1)

Вблизи равновесного состояния δ a_i = (a_i – a_i⁰) < < a_i , тогда А  можно разложить в ряд Тейлора:

 

        ,                         (3. 2)

 

где А₀ – значение параметра в равновесии, А_i и A_ik – постоянные коэффициенты разложения.

Если δ a_i очень мало, то можно ограничиться значением А₀ и отбросить все остальные члены ряда - этому состоянию соответствует область I на диаграмме, которая может рассматриваться, как сфера применения равновесной термодинамики в качестве описания исследуемых систем.

Если δ a_i  мало, но не настолько, чтобы можно было пренебрегать возмущениями первого порядка, то функцию A(a_i) следует представить в виде:

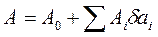      ,                                           (3. 3)

что демонстрирует линейную связь параметра системы с величиной отклонения от равновесия - процессы в этой области, обозначенной как область II, могут быть проанализированы с помощью линейных законов. К этой области относятся процессы, которые описываются с помощью линейной термодинамики (о ней ещё пойдёт речь ниже, поэтому здесь мы не расшифровываем этот термин).

       Дальнейший учёт членов разложения в случаях, когда отклонения от равновесия ещё больше, приводит к появлению нелинейных членов вида Aδ a_iδ a_k и т. д. в зависимости  A(a_i) (область III) - это значит, что в данной области на описание процессов не распространяется принцип суперпозиции, то есть сумма действий различных причин (влияния различных параметров) непропорциональна сумме их вкладов. В этом случае для описания процессов в неравновесных системах используют принципы нелинейной термодинамики неравновесных процессов.

       При дальнейшем росте δ a_i , когда перестает выполняться неравенство δ a_i < < a_i, невозможно представить величину А в виде сходящегося ряда – здесь отклонения от равновесия настолько велики и процессы происходят настолько интенсивно, что величину параметра А (т. е. измеряемую величину любого параметра), характеризующую всю систему в целом или её отдельную часть (элемент), невозможно описать однозначно (область IV). Рассмотрение процессов в этой области с точки зрения термодинамики встречается со значительными сложностями, однако современные методы анализа нелинейных математических моделей позволяют решать отдельные задачи и в этой далёкой от равновесия области.

       Подобное разграничение процессов в значительной степени условно – например, величина отклонения от равновесия, полагаемая для одних случаев малой, может оказаться значительной в других случаях. Однако такой подход позволяет расставить принципы описания по мере их усложнения в соответствии с основным критерием – степенью отклонения от равновесия. Рассмотрим последовательно возможные способы применения термодинамического описания при увеличении величины этого критерия.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: