4.3. Линейная термодинамика – определение термодинамических сил, 2-й и 3-й законы Онзагера.

 

Приведённый выше пример позволяет понять, почему причины возникновения потоков в линейной термодинамике названы силами – точнее, термодинамическими силами: в механическом аналоге термодинамической системы – механической диссипативной системе – обычная механическая сила и термодинамическая сила есть одно и тоже (идентичны). Однако приведённые выше экспериментально установленные законы (законы диффузии, теплопроводности, закон Ома) показывают, что причины возникновения потоков могут быть не связаны с механическими силовыми характеристиками системы. Что будут представлять собой термодинамические силы в этих случаях? Существует ли какое-либо правило определения термодинамических сил для рассматриваемой неравновесной системы? Чтобы ответить на эти вопросы, рассмотрим ещё одну (уже модельную) диссипативную механическую систему, поведение которой демонстрирует поведение стандартной неравновесной термодинамической модели (этот пример подробно рассмотрен в учебнике А. А. Жуховицкого /4/, здесь он приводится в сокращённом варианте). В стеклянную ёмкость с вязкой жидкостью (например, с глицерином или густым силиконовым маслом) помещено большое количество мелких железных шариков (дробинок), причём шарики однородно распределены в жидкости посредством перемешивания. Вязкость жидкости и размеры шариков подобраны таким образом, чтобы за время проведения опыта не происходило заметного оседания шариков под действием силы тяжести (т. е. шарики не тонут, а взвешены в жидкости). Количество шариков в единице объёма жидкости характеризуется величиной с [1/м³] – фактически это объёмная концентрация шариков (аналог частиц, молекул). Ёмкость с жидкостью и взвешенными в ней железными шариками помещена в однородное магнитное поле (рис. 4. 2):

Рис. 4. 2. Емкость с вязкой жидкостью и взвешенными в ней железными шариками в однородном магнитном поле.

Под действием внешнего магнитного поля шарики намагничиваются и начинают притягиваться к ближайшему магнитному полюсу, причём эта сила притяжения  имеет смысл механической силы X_N, действующей на шарики со стороны магнитного поля, и одинакова во всём объёме жидкости. Поскольку жидкость вязкая, скорость движения шариков v тоже одинакова и не меняется со временем - это означает, что вся затрачиваемая на перемещение шариков энергия тратится на трение внутри жидкости (см. выше диссипативную механическую систему). Напишем выражение для мощности и энергии dW, требуемой для движения шариков в единице объёма жидкости за время dt:

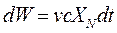
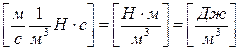            .               (4. 13)

 

В правой части выражения (4. 13) показана размерность полученной величины, которая имеет смысл энергии в единице объёма, или объёмной плотности энергии.  Произведение vc имеет размерность 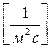, т. е. размерность потока шариков I. Тогда уравнение (4. 13) можно переписать в следующем виде:

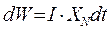                                                      .                               (4. 13а)

В результате движения шариков в вязкой жидкости вся энергия диссипирует, превращаясь в тепло, которое благодаря принципу локального равновесия может быть выражено через плотность энтропии:

                                    dW = δ Q = Tds.                      (4. 14)

После подстановки (4. 13а) в (4. 14) и деления обоих частей полученного уравнения на dt получим:

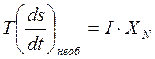                                    ,                              (4. 15)

где индекс «необ» при производной плотности энтропии по времени (скорости изменения энтропии при движении шариков) означает необратимость рассеяния энергии движения шариков, то есть необратимость её перехода в тепло. Полученное соотношение (4. 15) показывает связь между скоростью изменения параметра, введённого в классической термодинамике, то есть скоростью изменения энтропии (точнее, плотности энтропии) и параметрами, характеризующими отклонение системы от равновесия – потоком («удельной» скоростью) и силой (причиной возникновения потока). Энтропия – понятие чисто термодинамическое, а поток и сила – это динамические понятия, которые могут использоваться для получения динамической картины процесса. Таким образом, соотношение (4. 15) связывает воедино термодинамический (равновесный) и динамический (неравновесный) подходы в описании неравновесной системы.

       Очень заманчивым было стремление расширить соотношение связи между динамикой и термодинамикой на широкий круг неравновесных систем и процессов. Это сделал Онзагер, написав 2-ой закон линейной термодинамики –     2-ой закон Онзагера – в следующем виде:

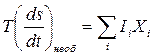                                              .                                      (4. 16)

2-ой закон Онзагера показывает, что скорость изменения плотности энтропии пропорциональна сумме произведений каждого из потоков, присутствующих в системе, на «свою» силу. Этот закон часто называют правилом определения термодинамических сил, поскольку именно с помощью 2-го закона Онзагера можно находить явное выражение для термодинамических сил, если задана конкретная неравновесная система. Рассмотрим пример того, как это делается, если система не включает в себя механических сил и соответствующих им потоков.

Рассмотрим проводник в однородном электрическом поле E. Сечение проводника имеет площадь f. В электрическом поле вдоль проводника в направлении x протекает ток i. Будем считать, что этот проводник представляет собой нагревательный элемент в термическом устройстве (в печи сопротивления), при этом переходит в тепло вся энергия электрического поля, которая расходуется на возбуждение электрического тока. Определим, сколько джоулевого тепла, в соответствии с законом Джоуля-Ленца, выделяет элемент провода длиной dx за время dt:

                                               .                                              (4. 17)

 

Если учесть, что для провода с током данного объема V = fdx имеется термодинамическая связь выделяемого тепла с энтропией δ Q=TdS, соотношение (4. 17) можно переписать в следующем виде:

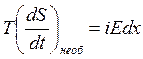                                               ,                                           (4. 18)

При делении обоих частей уравнения (4. 18) на V получим:

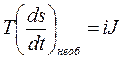                                                ,                                                (4. 19)

где s = S/V – плотность энтропии, а J = i/f – плотность тока. Плотность тока выражается как  J = I_e∙ e, т. е. является произведением потока зарядов (электронов) I_e на величину единичного заряда (заряда электрона) e, тогда окончательно

                                               .                                      (4. 20)

При сравнении выражения (4. 20) со 2-ым законом Онзагера легко заметить, что в правой части этого выражения записано произведение потока I_e (потока зарядов) на термодинамическую (электрическую) силу X_e = eE, которую в соответствии с электродинамикой можно выразить ещё одним способом X_e = – e 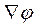 (φ – потенциал электрического поля).

Аналогичное      правило определения термодинамических сил (2-ой закон Онзагера) позволяет находить их вид и в других случаях: например, в химической системе, в которой отсутствуют «посторонние» силы, - т. е. нет других взаимодействий, кроме химических, - при постоянстве объёма и температуры (V = const, T = const) термодинамическая сила X_j, управляющая j–м потоком (скоростью j–й химической реакции) в данной системе, равна

                                                           X_j =  – Δ G_j,                                            (4. 21)

т. е. определяется изменением энергии Гиббса в j–й реакции. В случае термодиффузии, когда в системе есть поток тепла I_Q и поток i-го компонента вещества I_i, вывод выражений термодинамических сил также возможен - при помощи 2-го закона Онзагера удаётся найти вид тепловой силы X_Q и диффузионной силы X_i :

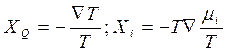                                          .              (4. 22)

       Итак, 1-й и 2-й законы Онзагера позволяют определить термодинамические потоки и термодинамические силы для рассматриваемой неравновесной системы при незначительных отклонениях от состояния равновесия (область II диаграммы Бокштейна) и указывают на их линейную связь между собой. Каков дальнейший путь анализа неравновесных систем? Алгоритм применения линейной термодинамики для описания неравновесных процессов следующий:

1. Определение потоков (и их размерностей), присутствующих в системе.
2. Определение термодинамических сил - общую схему этой операции можно представить следующим образом:

- для исследуемой системы в заданных условиях необходимо записать термодинамическое локальное уравнение Гиббса;

- далее требуется привести уравнения непрерывности, характеризующие законы сохранения массы, энергии, заряда и т. д.;

- выражения для потоков, которые надо получить путём преобразования уравнений непрерывности, следует подставить в уравнение Гиббса и свести его к уравнению баланса для плотности энтропии:

                                           ,                        (4. 23)

где I_s – поток энтропии;

- сравнить полученное уравнение со 2-ым законом Онзагера и определить выражения для термодинамических сил.

3. Записать уравнения для потоков и сил в системе в соответствии с 1-ым законом Онзагера. Решение полученной линейной системы позволяет определить неизвестные искомые величины, при этом коэффициенты Онзагера L_ik определяются из опытных данных или из модельных построений. Здесь следует привести третий и последний закон линейной термодинамики – 3-ий закон Онзагера, который имеет отношение к определению кинетических коэффициентов L_ik и является следствием принципа микрообратимости, то есть он формулируется следующим образом:

                                                        L_ik = L_ki ,                                              (4. 24)

что означает влияние i-й силы на k-ый поток такое же, как и влияние k-й силы на i-й поток - это аналог третьего закона Ньютона в механике. Принцип микрообратимости (для химических процессов он соответствует принципу детального химического равновесия) утверждает, что «в состоянии равновесия любой молекулярный процесс и обратный ему процесс протекают с одинаковой скоростью» (цитата из книги Б. С. Бокштейна «Диффузия в металлах», М., 1978 г. ) - таким образом, принцип микрообратимости и вытекающий из него 3-й закон Онзагера требуют, как и все остальные базовые положения линейной термодинамики, существования и соблюдение принципа локального равновесия. При этом 3-ий закон Онзагера позволяет сократить число кинетических коэффициентов, входящих в уравнения 1-го закона, что упрощает решение конкретных задач в рамках линейной термодинамики.

 

       4. 4. Линейная термодинамика – диффузионные задачи

 

       Диффузия часто является лимитирующим звеном разнообразных процессов, происходящих в металлических материалах при их получении, термической обработке, эксплуатации в условиях высоких температур, растягивающих и сжимающих механических напряжениях. Поэтому решению диффузионных задач всегда уделяется большое внимание. Какие дополнительные преимущества при описании диффузионных процессов даёт применение  линейной термодинамики? Чтобы ответить на этот вопрос, надо получить запись основного уравнения диффузии с использованием понятий линейной термодинамики, т. е. через термодинамические силы и потоки.

Пусть диффузия i-го компонента происходит в рассматриваемой системе при постоянной температуре T=const. Если в системе нет никаких других термодинамических сил, кроме диффузионной, то 1-ый закон Онзагера позволяет записать уравнение для единственного термодинамического диффузионного потока:

I_i = L_iDX_iD,

где X_iD – термодинамическая диффузионная сила, L_iD – кинетический диффузионный коэффициент. Согласно (4. 22), диффузионная сила в условиях постоянства температуры равна . Предположим также, что диффундирующее вещество – i-й компонент – находится в разбавленном растворе внутри основного базового компонента, тогда химический потенциал i-го растворённого компонента можно представить в следующем виде:

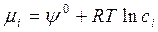                                          ,                              (4. 25)

где c_i – концентрация i-го компонента, Ψ ⁰ – значение химического потенциала в стандартном состоянии (постоянное для всей системы). Диффузионный поток в этом случае будетиметь вид:

                                          .                                              (4. 26)

Сравнение уравнения (4. 26) с законом диффузии (4. 8), полученным на основании экспериментальных данных, позволяет определить вид кинетического диффузионного коэффициента, который входит в 1-й закон Онзагера:

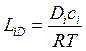                                              .                                                   (4. 27)

Окончательная подстановка термодинамической диффузионной силы и кинетического коэффициента в уравнение 1-г закона Онзагера позволяет получить для рассматриваемой системы выражение закона диффузии в следующем виде:

                                    .                                          (4. 28)

       Для демонстрации преимуществ применения полученной формы диффузионного уравнения рассмотрим конкретную задачу. Пусть тонкая металлическая плёнка нанесена путём вакуумного распыления на твёрдую подложку, которая изготовлена из того же металла, но содержащего небольшое количество легирующего элемента - концентрация легирующего элемента в металле подложки равна c_i . После нанесения плёнки, во время которого подложка нагрелась до предплавильной температуры, плёнка и подложка были охлаждены до температуры T, необходимой для проведения термической обработки. При этой температуре происходит диффузионное распространение легирующего элемента из подложки в пленку, причём процесс диффузии в плёнке протекает в присутствии механических напряжений σ , которые имеют термическую природу - они возникли в результате быстрого охлаждения металла плёнки до температуры T. Таким образом, распространение легирующего элемента происходит под действием перепада концентрации между подложкой и плёнкой (в начальный момент времени легирующий элемент в плёнке отсутствует), однако на него оказывает влияние также наличие механических напряжений в плёнке. Определим возникающий поток легирующего компонента, считая, что легирующий компонент образует в металле основы и плёнки разбавленный твёрдый раствор – тогда, согласно уравнению (4. 28), запишем выражение для химического потенциала растворённого компонента:

                        ,             (4. 29)

 

где дополнительный член (σ Δ V_акт) является вкладом в химический потенциал при диффузионном скачке атома, то есть при этом совершается работы против сил растяжения или сжатия в поле механических напряжений. Величина Δ V_акт называется активационным объёмом и представляет собой величину изменения объёма металла в момент диффузионного скачка атома, то есть величину возрастания объёма кристаллической решетки вблизи диффундирующего атома, чтобы он мог «просочиться» между соседями при однократном скачке (в записи химического потенциала активационный объём имеет размерность [м³/моль], т. е. характеризует изменение объема металла в расчёте на 1 моль диффундирующих атомов, причём при вакансионном механизме диффузии величина активационного объёма близка к атомному объёму Ω ). Далее найдём градиент химического потенциала при условии постоянства объёма системы:

                                         (4. 30)

Подставим его в уравнение для диффузионного потока, тполучим:

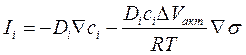                                 .                             (4. 31)

Выражение (4. 31) показывает, что при наличии механических напряжений диффузионный поток включает в себя две независимые части: первая – концентрационная часть - аналогична диффузионному потоку, возникающему вследствие градиента концентраций; в отсутствие напряжений концентрационная часть является единственной и представляет собой обычный закон диффузии (закон Фика). Вторая часть – это вклад градиента напряжений в общий поток.

Найдём условие установления стационарного (конечного) распределения концентрации легирующего элемента внутри тонкой пленки на поверхности металла подложки в результате диффузионного процесса. При стационарном состоянии общий поток I_i = 0, тогда из уравнения (4. 31) получим выражение для стационарного распределения концентрации c_i^s:

 

                                    .                       (4. 32)

Уравнение (4. 32) показывает зависимость стационарной концентрации легирующего элемента от напряжений в плёнке. Если известна эпюра напряжений, т. е. пространственное распределение напряжений в плёнке, то с помощью уравнения (4. 32) можно получить пространственное распределение установившихся концентраций легирующего элемента.

 

 

       4. 5 Линейная термодинамика – принцип Пригожина.

       Проанализируем поведение неравновесной системы, в которой имеются две термодинамические силы, которые вызывают появление двух термодинамических потоков. Для наглядности вновь остановимся на эффекте термодиффузии, и запишем уравнения 1-го закона Онзагера:

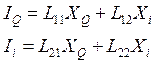                                                  ,                                 (4. 33)

 

где I_Q и X_Q – соответственно поток тепла и тепловая сила, а I_i и X_I – поток i-го компонента и диффузионная сила. Далее запишем уравнение 2-го закона Онзагера и подставим в него потоки из уравнений (4. 33). Также учтём, что в соответствии с 3-им законом Онзагера  L₁₂ = L₂₁, тогда:

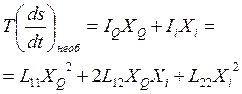                        .          (4. 34)

 

Полученная квадратичная форма для термодинамических сил имеет положительный знак, что следует из 2-го закона термодинамики, согласно которому самопроизвольное изменение энтропии (плотности энтропии, в соответствии с принципом локального равновесия ), а следовательно, и величина 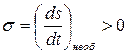 при необратимых процессах. Величина σ , которую мы ввели для обозначения скорости изменения плотности энтропии, носит название плотности производства энтропии, а соответствующая макроскопическая величина  - производства энтропии. В дальнейшем мы всегда будем использовать именно эти обозначения и названия для скоростей изменения энтропии.

       Пусть X_Q = const (тепловая сила не меняется со временем - например, внешние условия таковы, что разница температур на границах системы остаётся постоянной), тогда условием стационарности будет отсутствие диффузионного потока I_i = 0. Определим, какое значение принимает плотность производства энтропии σ в стационарном состоянии. Для этого, считая диффузионную силу единственным параметром, который может влиять на поведение системы, найдём производную плотности производства энтропии σ по X_i  :

             .                    (4. 35)

Таким образом, при X_Q = const производная σ пропорциональна значению диффузионного потока. Но в стационарном состоянии I_i = 0, то есть тогда зависимость плотности производства энтропии от диффузионной силы имеет экстремум. А так как 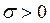 во всей области существования, то экстремум является минимумом (см. рис. 4. 3):

 

Рис. 4. 3. Зависимость плотности производства энтропии от диффузионной силы.

Данное рассмотрение позволяет сделать вывод, что стационарному состоянию соответствует минимум плотности производства энтропии. Приведённый пример можно обобщить на произвольное число независимых термодинамических сил, кроме того, производство энтропии для всей системы 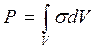также подчиняется данному принципу. Приведём общую формулировку этого принципа, который носит название принципа Пригожина : стационарное состояние системы, в которой происходит необратимый процесс, характеризуется тем, что производство энтропии имеет минимальное значение для заданных внешних условий, препятствующих переходу системы в равновесное состояние. Принцип Пригожина свидетельствует о том, что стационарное состояние, описываемое линейной термодинамикой, является устойчивым: если внешними силами вывести систему из стационарного состояния, изменив какой-либо внешний параметр, то система снова возвратится в первоначальное состояние. Принцип Пригожина полностью согласуется с эмпирическим правилом, носящим название принципа Ле-Шателье: при внешнем воздействии на систему, находящуюся в стационарном состоянии, в ней возникают внутренние потоки, возвращающие её в стационарное состояние.

       Итак, в результате краткого рассмотрения неравновесных систем в области малых отклонений от состояния равновесия (линейная область II диаграммы Бокштейна) можно сделать заключение, что здесь поведением системы управляет стремление к единственному стационарному состоянию, характеризующемуся минимумом производства энтропии. При этом в эволюции системы нет особенностей: она либо находится в стационарном состоянии неограниченно долго, либо монотонно стремится к этому состоянию.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: