6.2. Самоорганизация – эффект Бенара

       Одним из первых экспериментально обнаруженных явлений такого рода стал гидродинамический эффект, исследованный Бенаром в 1900 году и названный его именем.        Эффект Бенара заключается в следующем. В емкость небольшого диаметра (15-20 см) налита тонким  (0, 5 см) слоем вязкая жидкость - например, силиконовое масло. Если теперь однородно нагревать дно емкости, а внешнюю поверхность масла оставить открытой, то через слой масла снизу вверх будет протекать тепловой поток Q (вдоль оси z, рис. 6. 3), который отводится через внешнюю поверхность, так как её температура T₂ ниже, чем температура дна сосуда T₁:

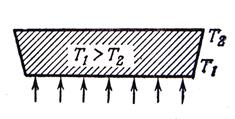
6. 3. Самоорганизация – эффект Бенара.

Так как слои масла, расположенные у самого дна, нагреты сильнее, чем поверхностные, то их плотность меньше, поэтому возникает архимедова выталкивающая сила, и масло со дна стремится подняться вверх (конвекция), но этому препятствует вязкость  - в результате, при небольших перепадах температуры Δ T = T₁ – T₂ тепло в слое масла распространяется только посредством теплопроводности. Однако при дальнейшем увеличении Δ T наступает момент, когда вязкость оказывается больше не в состоянии сдерживать выталкивающую силу, и процесс скачком переходит в фазу конвективной теплопередачи, при этом величина проходящего через систему теплового потока Q скачком возрастает (рис. 6. 4):

Рис. 6. 4. Зависимость теплового потока в опыте Бенара от перепада температур между нагреваемой и открытой поверхностями жидкости.

При этом скачком меняется и макроскопическая структура жидкости если в течение всей стадии теплопроводности внешняя поверхность жидкости выглядела совершенно однородным слоем, то сразу после перехода к конвективной стадии теплопередачи поверхность разбивается на шестиугольные ячейки, центрированные точками посередине (рис. 6. 5). Эта ячеистая структура на поверхности масла хорошо видна, если добавить в него некоторое количество мелкого алюминиевого порошка:

                         а                                                                           б

Рис. 6. 5. Ячейки Бенара: а - фото ячеек Бенара, вид сверху, б - конвекция Бенара при увеличении ^х25: свет, отражённый от алюминиевых хлопьев, демонстрирует подъём жидкости в центре каждой ячейки и её опускание на краях.

В центре каждой ячейки конвективные потоки выходят на поверхность, затем, двигаясь к границам ячеек, они отдают вынесенное снизу тепло, охлаждаются и, сталкиваясь там с потоками соседних ячеек, опускаются вниз, чтобы повторить весь цикл, забрав очередную порцию тепла.

Таким образом, мы видим, что в системе (в сосуде с вязкой жидкостью, нагреваемом снизу) при достижении внешним параметром критического значения Δ T_кр происходит самопроизвольное образование упорядоченной структуры – самоорганизация. В первоначально однородной жидкости никакого намека или плана образования данного порядка не было. Посмотрим, разрешён ли данный процесс самоорганизации с точки зрения термодинамики. Изменение энтропии внутри самой системы d_iS ≥ 0 при любых процессах, но изменение энтропии, связанное с прохождением через неё теплового потока, определяется выражением (в предположении, что передача тепла от горячего дна сосуда жидкости и от нагретой жидкости во внешнюю среду происходит обратимо):

.       (6. 3)

Таким образом, система отдаёт энтропию, и чем больше Δ T, тем больше - значит, самоорганизация термодинамикой не запрещена, лишь бы потери энтропии оказались больше, чем её рост из-за релаксационных процессов внутри жидкости (см. уравнение (6. 1).

       Для определения момента скачкообразного перехода к упорядоченной структуре, вне зависимости от конкретных условий проведения опыта, исследуют зависимость безразмерного градиента температуры – числа Рэлея

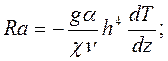 так как в данном случае 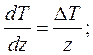то    (6. 4)

от безразмерного теплового потока – числа Нуссельта

,                                          (6. 5)

где α и χ – коэффициенты теплового расширения и теплопроводности, h – толщина слоя масла, Q₀ – поток тепла, переносимый посредством теплопроводности. Эмпирическая зависимость Nu = f(Ra) представлена на рис. 6. 6. В точке Ra = Ra_кр эта зависимость, представляющая до этого прямую, параллельную оси абсцисс, приобретает скачком наклон, что соответствует динамическому неравновесному переходу процесса теплопереноса от теплопроводности к конвекции, при котором спонтанно возникает ячеистая структура конвективного течения.

Рис. 6. 6. Зависимость числа Нуссельта от числа Рэлея в опыте Бенара