4.2. Линейная термодинамика – первый закон Онзагера

       Рассмотрим произвольную неравновесную систему, через которую проходит несколько различных потоков I_j. Раз имеются потоки, значит, есть и причины, их вызывающие - термодинамические силы X_j. Как связаны потоки с силами, в общем случае неизвестно, поэтому представим эту зависимость следующим образом:

                                                  (4. 5)

Термодинамические силы вызывают потоки, которые являются индикаторами неравновесности, поскольку в отсутствие сил система самопроизвольно релаксирует к равновесию, какое бы не было её начальное состояние.

Пусть силы малы, то есть система незначительно отклонена от состояния равновесия (области II и III диаграммы Бокштейна). Тогда функцию F(X_j) можно представить в виде ряда Тейлора, разложив её вблизи состояния равновесия по X_j:

                         (4. 6)

где 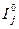- потоки при отсутствии термодинамических сил (при условии X_j=0 они также отсутствуют, тогда 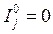). Рассмотрим область II диаграммы Бокштейна, в которой отклонения от равновесия – термодинамические силы – малы настолько, что в разложении любого термодинамического параметра можно учитывать только линейные члены (уравнение (3. 2)). Тогда из (4. 6) получим:

                                             (4. 7)

       Уравнение (4. 7) является первым постулатом линейной термодинамики, которая была развита в работах Л. Онзагера в 30-х годах 20-го столетия и поэтому носит его имя – первый закон Онзагера. 1-й закон Онзагера показывает, что при малых отклонениях от состояния равновесия термодинамические потоки линейно зависят от термодинамических сил, причём на каждый поток влияют все силы, присутствующие в рассматриваемой системе. Коэффициенты  называют кинетическими коэффициентами, поскольку они показывают интенсивность вляияния силы X_k на поток I_J в динамике. Тот факт, что потоки I_j (термодинамические потоки в неравновесной термодинамике) пропорциональны некоторым движущим силам (термодинамическим силам Х_к), хорошо известно, поскольку существуют эмпирически установленные законы:

Закон диффузии (закон Фика) - поток i-го компонента вещества пропорционален градиенту его концентрации:

                                                (4. 8)

где D_i – коэффициент диффузии.                                                                                        

Закон теплопроводности (закон Фурье) – поток тепла пропорционален градиенту температуры:

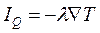                              (4. 9)   

где l - коэффициент теплопроводности.                                                                                       

      Закон электропроводности (закон Ома) – поток носителей заряда (электрический ток) пропорционален градиенту потенциала электрического поля φ :

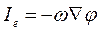                                            (4. 10) 

где ω – коэффициент электропроводности (электрическая проводимость).

       Во всех этих законах потоки линейно зависят от градиентов (концентрации, температуры, потенциала электрического поля), которые являются причинами появления потоков. Сравнивая эти эмпирические законы с первым законом Онзагера, можно предположить, что именно градиенты скалярных величин c_i, T, φ являются основными составляющими термодинамических сил X_k, в результате которых возникают векторные потоки I_i, I_Q и I_e. Известны и другие аналогичные законы, установленные опытным путем для различных необратимых процессов, которые также характеризуются линейными соотношениями между причиной (силой) и следствием (потоком) - значит, Онзагеру удалось обобщить все эти эмпирические законы и получить для них общее выражение (4. 7), которое легло в основу линейной термодинамики в качестве первого постулата неравновесной термодинамики. При этом 1-ый закон Онзагера дополнительно указывает на то, что существуют перекрёстные линейные связи между силами и потоками - например, возможно появление диффузионного потока вещества при наличии в системе градиента (перепада) температуры. Действительно, такие эффекты обнаружены в опытах и имеют место быть -например, эффект возникновения потока вещества в результате неоднородности температурного поля называется термодиффузией.  

Для более ясного понимания характера термодинамических величин, которые используются в 1-ом законе Онзагера, рассмотрим пример использования этого закона для простой механической системы. Пусть тело массой m движется с трением (т. е. мы рассматриваем диссипативную механическую систему) прямолинейно по направлению x под действием силы F. Будем считать, как это часто делается в задачах механики, что сила трения пропорциональна скорости движения (закон вязкого трения в воздухе или воде), тогда уравнение движения можно записать в следующей форме:

                                               ,                             (4. 11)

где 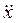 - ускорение движения тела,  - его скорость, γ – коэффициент трения. Рассмотрим случай равномерного движения, когда вся кинетическая энергия движения уходит на сопротивление трению (происходит полное рассеяние энергии с переходом в тепло), тогда:

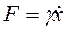                                                 или  .                          (4. 12)

Сравним полученное уравнение движения с 1-ым законом Онзагера, записанным для наличия в системе одной силы, вызывающей один поток - I = LX. Сопоставление этих уравнений приводит к сопоставлению величин, подобных по смыслу:

       Термодинамический поток соответствует скорости ,

       Термодинамическая сила – механической силе ,

       Коэффициент Онзагера обратно пропорционален коэффициенту трения .

Таким образом, закон Онзагера оказывается справедливым и для диссипативной механической системы, при этом термодинамическая сила равна механической (ньютоновской) силе (обозначим её как X_N).