5. Область нелинейных законов – универсальный критерий эволюции систем

       Проведём рассмотрение систем, для которых отклонения от состояния равновесия по одному или нескольким параметрам таковы, что связь между термодинамическими потоками и вызывающими их термодинамическими силами перестаёт быть линейной (область III на диаграмме Бокштейна), то есть не выполняется 1-ый закон Онзагера. Как показали Гленсдорф и Пригожин, поведение таких систем подчиняется так называемому Универсальному критерию эволюции, который является расширением принципа Пригожина в линейной термодинамике на нелинейную область. Для формулировки У ниверсального критерия эволюции запишем выражение для полного производства энтропии P в открытой системе:

                        .                           (5. 1)

Продифференцируем уравнение (5. 1) по времени:

,    (5. 2)

где первый член выражения – скорость изменения производства энтропии, обусловленная изменением термодинамических сил, а второй - скорость изменения производства энтропии, связанная с изменением потоков в системе. В области, где существуют линейные связи сил и потоков, оба вклада в скорость изменения производства энтропии одинаковы, что следует из выражения:

.    (5. 3)

В соответствии с принципом Пригожина 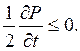 В общем случае, когда мы не ограничиваем область рассмотрения:

                                                .                                               (5. 4)

Это неравенство и является формулировкой Универсального критерия эволюции. Гленсдорфа – Пригожина, физический смысл которого такой: в любой неравновесной системе с фиксированными граничными условиями процессы идут так, что скорость изменения производства энтропии, обусловленная изменением термодинамических сил, уменьшается, т. е. 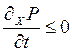; знак равенства относится к стационарному состоянию.

       Покажем справедливость этого критерия для системы, через которую проходит поток тепла I_Q. В этом случае скорость изменения производства энтропии, зависящая от изменения термодинамических сил, имеет вид:

.                   (5. 5)

По теореме Гаусса-Остроградского

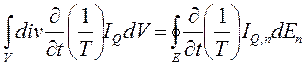,      (5. 6)

где E – граница системы; n – направление нормали к границе. Интеграл вдоль границы E с фиксированной температурой обращается в «0». Кроме того, из уравнения непрерывности следует, что

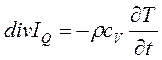                        ,                                                 (5. 7)

где ρ – плотность [кг/м³],  c_V – удельная теплоемкость [Дж/кг∙ К]. Таким образом,

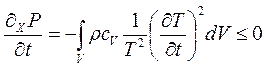             .                            (5. 8)

       В равновесной или линейной термодинамике поведение системы можно описать с помощью потенциала: G – это энергия Гиббса для равновесных систем, P – производство энтропии для линейных неравновесных систем. В области нелинейной термодинамики ввести потенциал в общем случае не представляется возможным: это связано с тем, что в соответствии с (5. 2) для сил определяет только часть прироста энтропии. Только в некоторых специальных случаях, когда является полным дифференциалом, удаётся ввести локальные потенциалы с экстремальными свойствами, описывающие систему в неравновесной области.

       Пусть исследуемая система такова, что в некоторой области изменения параметра a её поведение можно описать с помощью потенциала φ (рис. 5. 1). Пусть потенциал φ имеет два минимума: более глубокий (a⁰) назовём глобальным, менее глубокий (a^s) – локальным, при этом будем считать, что глобальный минимум соответствует термодинамическому равновесию системы. Отметим, что на потенциальной кривой имеется ещё один экстремум – максимум. Механическим аналогом такой формы потенциала является профиль местности, моделирующий холм с двумя впадинами по разные стороны от его вершины, при этом система (её аналог - шарик) будет стремиться занять положение с минимальным значением потенциала независимо от того, рассматриваем ли мы механический или неравновесный термодинамический вариант модели. В зависимости от величины отклонения от положения равновесия система может вести себя различным образом: она может возвращаться в равновесное состояние, если её начальное положение находится слева от максимума потенциала, либо может перескакивать в положение локального минимума (устойчивое стационарное состояние), если находится чуть правее максимума. Оба состояния при a⁰ и при a^s отвечают условию 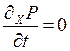, а при переходных процессах между ними . Кроме того, при максимальном значении потенциала также 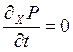, т. е. система также находится в стационарном состоянии, однако любое отклонение параметра a от максимума потенциала приводит к движению системы в сторону ближайшего минимума. Это особенно хорошо видно, если рассматривать механический аналог модели - значит, положение максимума соответствует неустойчивому положению системы. К неустойчивости может приводить изменение внешних условий или термодинамических сил: например, если в результате каких-либо причин происходит трансформация формы потенциала, показанного на рис. 5. 1а, к виду на рис. 5. 1б (механический аналог - часть склона размыло дождём), то в точке перегиба, которая образовалась на месте локального минимума, тоже выполняются условия стационарности, но положение системы в этой точке уже не является устойчивым:

Рис. 5. 1. Зависимость потенциала φ нелинейной неравновесной системы от параметра a.

       Итак, мы вышли за пределы линейных термодинамических моделей, в результате чего установили, что появились дополнительные особенности в поведении систем. Укажем некоторые из них.

Во-первых, может существовать несколько стационарных состояний, которые могут быть потенциально возможными путями развития процессов в заданной системе - это является следствием нелинейности моделей, приводящей к множественности возможных решений. Поведение системы, её переходы между стационарными состояниями зависят от начальных условий и всегда определяются Универсальным критерием эволюции Гленсдорфа-Пригожина.

Во-вторых, не все стационарные состояния являются устойчивыми, т. е. часть стационарных состояний, которые можно определить как результат решения нелинейной  термодинамической задачи, не описывают окончательное положение (поведение) системы и оказываются неустойчивыми. Механические аналоги помогают продемонстрировать такие возможности: существует устойчивое механическое равновесие (шарик находится в ямке) и неустойчивое механическое равновесие (шарик находится на вершине холма, и любое незначительное его смещение в сторону от наивысшей точки приводит к скатыванию вниз).

В-третьих, изменение внешних условий может менять вид устойчивости стационарных состояний - переводить устойчивые состояния в неустойчивые и наоборот.

       Представленные особенности не являются единственными - для наглядности были рассмотрены самые простые примеры, дающие только общее качественное описание нелинейных систем. Вместе с тем, поведение систем в нелинейной области может иметь значительно более сложные и разнообразные формы, процессы могут развиваться по нескольким альтернативным путям, которые реализуются в зависимости от значений и взаимосвязей внешних и внутренних параметров.