 |
Лагранжево и эйлерово описания движения сплошной среды
|
|
|
|
В рамках механики сплошной среды все частицы сплошной среды отличимы друг от друга – индивидуализируемы. Каждой индивидуальной частице сплошной среды ставится в соответствие упорядоченная тройка чисел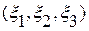 
. Эта тройка называется лагранжевыми координатами индивидуальной частицы. Лагранжевы координаты используются, чтобы указать эту частицу, т. е. служат ее “именем”, так же, как номера служат “именами” частиц, когда последние расположены дискретно. В качестве лагранжевых координат частицы 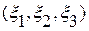обычно используются пространственные координаты точки 
, в которой эта частица находилась в начальный момент времени 
.
Как известно, движение сплошной среды и происходящие процессы описываются полями физических величин (скорости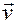 
, давления 
, плотности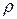 
, температуры 
и т. д. ).
Лагранжев подход.
Если эти величины рассматриваются как функции лагранжевых координат 
и времени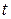 
, то описание называется лагранжевым или материальным. Таким образом, если 
и т. д., то это лагранжево описание движения сплошной среды. При этом подходе события описываются как происходящие с индивидуальными частицами. Основной кинематической характеристикой при лагранжевом описании является закон движения сплошной среды, т. е. зависимость пространственных координат от лагранжевых и времени:
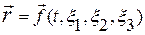или в координатной записи 
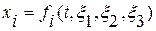, где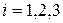 
.
Тогда скорость и ускорение частиц сплошной среды определяются соотношениями:
, где вектор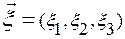 
.
По определению скорость изменения некоторой величины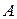 
в индивидуальной частице сплошной среды (т. е. при фиксированных значениях лагранжевых координат) называется индивидуальной, или материальной, или полной производной по времени от величины 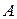и обозначается 
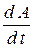(в некоторых книгах обозначается 
).
|
|
|
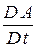При лагранжевом описании (т. е., когда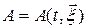 
) полная производная величины 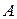по времени 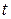равна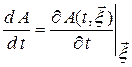 
по определению.
Эйлеров подход.
При эйлеровом описании (иногда говорят пространственном описании ) физические величины рассматриваются как функции пространственных координат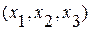 
и времени 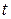. При этом подходе события описываются как происходящие в точках пространства. Основной кинематической характеристикой при эйлеровом описании является поле скорости 
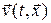, где 
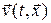. Вектор скорости - это скорость частицы сплошной среды, которая в момент времени 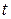находится в точке пространства с координатами .
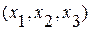Переход от лагранжева описания к эйлеровому:
Для того, чтобы перейти от лагранжева описания к эйлеровому, нужно соотношения, выражающие закон движения 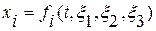, где 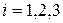, разрешить относительно лагранжевых координат, т. е. найти функции 
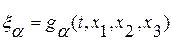, где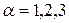 
. Тогда для любой величины 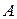, лагранжево описание которой 
известно, эйлерово описание находится как сложная функция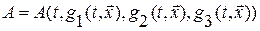 
.
Переход от эйлерова описания к лагранжеву:
Для того, чтобы перейти от эйлерова описания к лагранжеву, нужно найти решение системы обыкновенных дифференциальных уравнений
, где 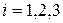(0. 1. 0)
с начальными условиями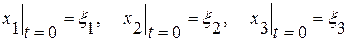 
.
Полученное решение 
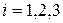, и есть закон движения сплошной среды, а - лагранжевы координаты частиц. Тогда для любой величины 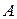, эйлерово описание которой 
известно, лагранжево описание находится как сложная функция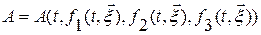 
.
Вычисление полной производной 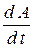величины 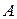по времени при эйлеровом описании ( т. е., когда 
):
При вычислении полной производной в эйлеровом описании используем:
- определение закона движения среды , ,
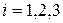- определение компонент вектора скорости
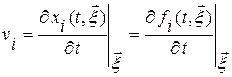
тогда по определению полной производной имеем:
|
|
|
т. е., 
,
или в сокращенной записи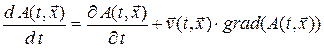 
, (0. 1. 1)
где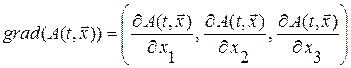 
- вектор градиента величины ,
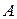- вектор скорости среды.
Полученная формула (0. 1. 1) для полной производной величины 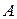при эйлеровом описании может быть озвучена так: скорость изменения величины 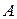в индивидуальной частице сплошной среды при эйлеровом описании равна скорости изменения величины 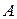в той точке эйлерова пространства, в которой в данный момент находится индивидуальная частица( слагаемое 
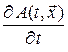), плюс скорость изменения величины за счет переноса в данную точку пространственного изменения величины 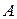в результате макроскопического движения сплошной среды (слагаемое 
).
Пример: выберем в качестве величины 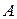вектор скорости среды 
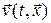. Тогда формула (0. 1. 1) дает выражение для вектора ускорения 
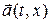при эйлеровом описании
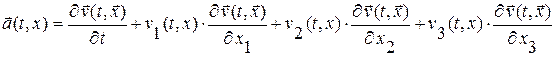
Напомним, что траекторией частицы называется геометрическое место ее положений во все моменты времени. Находятся траектории из решения приведенной выше задачи Коши для системы уравнений (0. 1. 0), из которой, в частности, следует, что вектор скорости в каждый момент времени направлен по касательной к траектории частицы. Более того, данное определение траектории позволяет нам интерпретировать полную производную как оператор дифференцирования по времени вдоль траектории частицы. Выпишем этот оператор:
(0. 1. 2)
Формула (0. 1. 2) теперь без особого труда может быть обобщена на случай дифференцирования вдоль произвольной параметрически заданной кривой в эйлеровом пространстве:
Пусть кривая задана соотношениями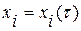 
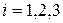, , где 
- параметр. Тогда
оператор полного дифференцирования вдоль кривой 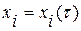примет вид 
(0. 1. 3)
применительно к любой функции 
.
Если функция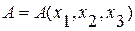 
явно не зависит от параметра , то формула (0. 1. 3) упрощается до вида 
.
|
|
|
