Сравнительных анализ некоторых свойств квазилинейной и линейной систем уравнений одномерной газовой динамики.

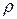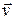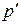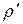Для существования исходной нелинейной системы уравнений движения (квазилинейной) требовалось, чтобы ,  и  (или ) были бы непрерывными функциями вместе со своими первыми производными, т. е. принадлежали к классу . Для волновых уравнений требовалось, чтобы искомые функции были дважды дифференцируемыми функциями. Наша система линеаризованных уравнений требует от искомых функций  (или ) и  непрерывности и один раз дифференцируемости.

Для одномерного плоского одноэнтропического течения идеального газа (жидкости)

линейная (линеаризованная) система уравнений движения имеет вид

,                                                                                                    (1. 26)

(имеется два семейства действительных характеристик, система двух уравнений для двух искомых функций гиперболического типа или два волновых уравнения  для одной функции каждое, где волновой оператор 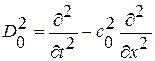, или одно волновое уравнение для потенциала скорости ).

Исходная квазилинейная система уравнений (нелинейная относительно )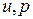

, где

.

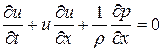Для квазилинейной гиперболической системы уравнения движения были выведены в предположении, что ,  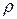и (или 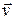) были бы непрерывными функциями вместе со своими первыми производными класса .

Отметим некоторые свойства рассматриваемой линейной гиперболической системы. Для линеаризованной системы уравнений требуется, чтобы искомые функции были бы непрерывны и допускали бы один раз дифференцирование. Если начальные условия задачи Коши таковы, что содержат разрыв первых производных первого рода (т. е. конечный разрыв производных первого порядка), то такой разрыв называется слабым.

1. Слабый разрыв, как мы показали, распространяется только по характеристикам.

2. Пусть, напр., характеристика  несет разрыв первых производных первого рода — слабый разрыв, а вне  решение такое, что функции принадлежат классу . Тогда для уравнений движения можно обобщить решение, включив в него и характеристику . Такое решение называется обобщенным решением уравнений движения.

3. Слабые разрывы не могут исчезнуть, если они были в начальных условиях и не могут возникнуть внутри характеристического треугольника, если их не было в начальных условиях.

4. Если терпят разрыв вторые и высшие производные, то эти разрывы распространяются только по характеристикам.

Замечание. Даже при отсутствии слабых разрывов на начальном отрезке AB для квазилинейных уравнений внутри характеристического треугольника может возникнуть разрыв первых производных.

В случае сильных разрывов (разрывов первого рода) мы получили следующие свойства для нашей линейной гиперболической системы:

1. Сильный разрыв распространяется только по характеристикам.

2. Пусть, например, сильный разрыв распространяется по характеристике . Тогда для линейной системы можно обобщить решение, включив в него и ударную волну . Причем для нашей системы соответствующий инвариант Римана не терпит разрыва. Такое решение называется обобщенным решением линейной гиперболической системы.

3. Сильный разрыв не может исчезнуть, если он был в начальных условиях и не может возникнуть, если его не было в начальных условиях линейной гиперболической системы, т. е. для линейной гиперболической системы справедливы для сильных разрывов те же положения, что и для слабых разрывов.

Отметим, что для исходной квазилинейной гиперболической системы эти положения не имеют места, а именно:

I. Сильный разрыв распространяется не по характеристикам. Эти линии сильного разрыва трудно обсчитывать (как численно, так и аналитически).

II. Сильный разрыв в начальных условиях может сразу исчезнуть и решение кроме начальной кривой будет всюду непрерывное.

III. Сильный разрыв может появиться в характеристическом треугольнике, когда на начальной кривой решение было всюду непрерывно.