 |
Инварианты Римана для линеаризованной системы уравнений одномерной газовой динамики для случая плоской симметрии ( ).
|
|
|
|
Инварианты Римана для линеаризованной системы уравнений одномерной газовой динамики для случая плоской симметрии ( ).
Введем новые неизвестные функции  и
и 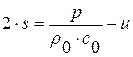 , получившие название инварианты Римана. Тогда условия совместности в системе (1. 71)
, получившие название инварианты Римана. Тогда условия совместности в системе (1. 71)
перепишутся в виде
 и
и  , где
, где  и
и 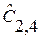 - постоянные (1. 73)
- постоянные (1. 73)
Вернемся к нашей исходной линеаризованной системе (1. 26):

Умножим первое уравнение этой системы на  и сложим со вторым, получим
и сложим со вторым, получим
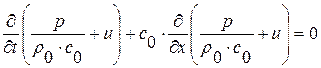
Теперь из первого вычтем второе, получим

Вспомним определение новых функций 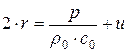 и
и 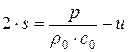 , тогда получим для r и s систему
, тогда получим для r и s систему
 (1. 74)
(1. 74)
Характеристики первого уравнения - семейство  , т. е.
, т. е.  , общее решение уравнения
, общее решение уравнения  ; для второго уравнения характеристики – семейство
; для второго уравнения характеристики – семейство 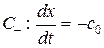 , т. е.
, т. е.  , общее решение
, общее решение 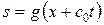 , где f и g любые дифференцируемые функции. Зная r и s, найдем
, где f и g любые дифференцируемые функции. Зная r и s, найдем  и u.
и u.
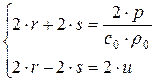

Как уже отмечалось, функции r и s называются инвариантами Римана. Вдоль каждой характеристики неизменны вдоль  — инвариант r, вдоль
— инвариант r, вдоль 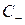 — инвариант s.
— инвариант s.
При 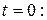
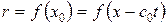 ,
,  . Эти формулы также как и формулы (1. 72) показывают, что
. Эти формулы также как и формулы (1. 72) показывают, что
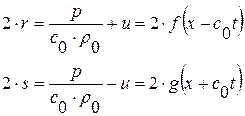
т. к. вдоль 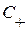 имеем
имеем 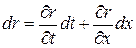 , где
, где 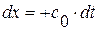 или
или  ; Аналогично
; Аналогично  .
.
Итак, постоянное значение r распространяется вправо со скоростью 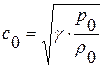 , постоянное значение s распространяется влево со скоростью
, постоянное значение s распространяется влево со скоростью  . Величину
. Величину  называют скоростью распространения звуковой волны или, сокращенно, скоростью звука.
называют скоростью распространения звуковой волны или, сокращенно, скоростью звука.
В нашем линейном случае все характеристики 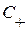 параллельны, поэтому все возмущения r идут с одной и той же скоростью
параллельны, поэтому все возмущения r идут с одной и той же скоростью  , т. е. возмущения для r идут без искажения. Аналогично для
, т. е. возмущения для r идут без искажения. Аналогично для 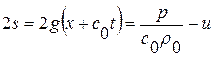 постоянные значения s идут по
постоянные значения s идут по 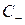 - характеристикам со скоростью
- характеристикам со скоростью 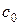 влево без искажения. Зная r и s, получим
влево без искажения. Зная r и s, получим
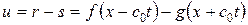 (1. 75)
(1. 75)
|
|
|
 (1. 76)
(1. 76)
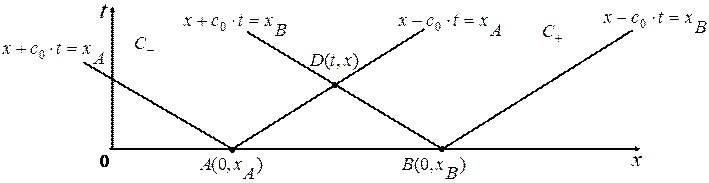 Конечно, по известному значению давления (1. 76) можно найти и плотность
Конечно, по известному значению давления (1. 76) можно найти и плотность 
Рис. 2. 6
На Рис. 2. 6 изображен характеристический треугольник 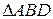 и характеристики обоих семейств.
и характеристики обоих семейств.
Попробуем теперь определить функции f и g таким образом, чтобы полученное решение (1. 75), (1. 76) удовлетворяло условиям задачи Коши при задании начальных значений  и
и  на отрезке AB (или на всей оси Ox).
на отрезке AB (или на всей оси Ox).
Решение задачи Коши для линейной системы (1. 26) при помощи инвариантов Римана.
Начальные данные (при ).
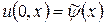 на AB (или на всей оси Ox),
на AB (или на всей оси Ox),
 на AB или на всей оси Ox.
на AB или на всей оси Ox.
Решение: Из (1. 75), (1. 76) при  имеем:
имеем:
 ,
,
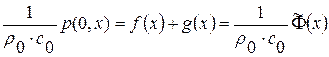 .
.
Сложим эти два уравнения и разделим на двойку, получим
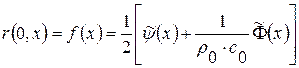 .
.
Затем вычтем 1-ое уравнение из 2-го и разделим на два, получим
 .
.
При  , учитывая, что r постоянен вдоль
, учитывая, что r постоянен вдоль 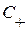 и s постоянен вдоль
и s постоянен вдоль  получим:
получим:
 ,
,
 .
.
Поэтому
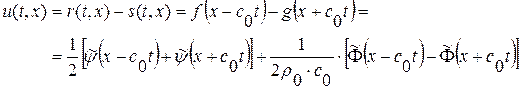 (1. 77)
(1. 77)
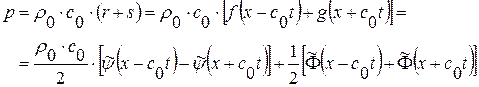
Получили решение задачи Коши, когда заданы начальные данные на отрезке AB (или на всей оси x) для возмущения давления  и возмущения скорости
и возмущения скорости  .
.
Сравним полученное решение (1. 77) с найденным ранее решением аналогичной задачи Коши для волнового уравнения относительно потенциала скорости 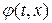 :
:
в дифференциальной форме  для гладкой
для гладкой 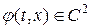
или в интегральной форме 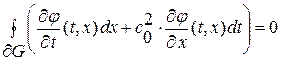 для кусочно-гладкой
для кусочно-гладкой 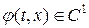 .
.
Начальные условия для обоих типов уравнений одинаковы:
 (1. 34. 2)
(1. 34. 2)
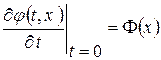
Решение для обоих типов уравнений с начал. условиями (1. 34. 2) имеет одинаковый вид:
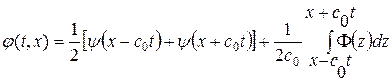 (1. 35)
(1. 35)
Вспомнив дифф. связи между  вида
вида 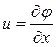 ,
, 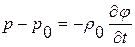 , (**)
, (**)
найдем из решения (1. 35) искомые производные  и
и  :
:
 (1. 78)
(1. 78)
где символом штрих обозначена обыкновенная производная,  ,
,  .
. 
 (1. 79)
(1. 79)
Установим связь между начальными функциями  ,
, 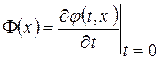 и функциями
и функциями 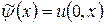 ,
, 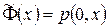 . Из (**) следует, что
. Из (**) следует, что 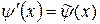 и
и 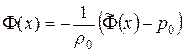 . Тогда, подставляя в формулы (1. 78) и (1. 79) найденную связь между начальными функциями и учитывая (**) мы получим формулы (1. 77), что окончательно подтверждает совпадение полученных разными путями решений одной и той же задачи Коши.
. Тогда, подставляя в формулы (1. 78) и (1. 79) найденную связь между начальными функциями и учитывая (**) мы получим формулы (1. 77), что окончательно подтверждает совпадение полученных разными путями решений одной и той же задачи Коши.
|
|
|
Заметим, что все приведенные выше рассуждения и выкладки, связанные с инвариантами Римана, сохраняют свою силу при замене участвующих в них исходных переменных на их возмущения. Это связано с тем, что как возмущения, так и сами переменные удовлетворяют одинаковым системам дифференциальных уравнений (1. 25) и (1. 26) при условии, что невозмущенное состояние газа соответствует состоянию покоя с постоянными значениями давления, плотности и равной нулю скорости.
Таким образом, в переменных возмущений 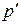 и
и  (т. к.
(т. к.  ) мы имеем:
) мы имеем:
 ,
, 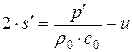 и, как следствие постоянства инвариантов Римана вдоль соответствующих характеристик, получаем решения в виде суммы бегущих волн
и, как следствие постоянства инвариантов Римана вдоль соответствующих характеристик, получаем решения в виде суммы бегущих волн
 ,
, 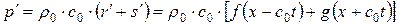 .
.
Рассмотрим несколько примеров, в которых для удобства иллюстрации основных свойств решений мы используем не сами исходные переменные, а их возмущения:
1. Рассмотрим частный случай, когда во всей области  (т. е. когда
(т. е. когда 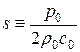 ). В этом случае
). В этом случае 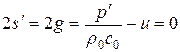 , во всей области. Такое частное решение называется особым, т. к., в отличие от общей постановки задачи Коши, в нашем случае начальные условия при
, во всей области. Такое частное решение называется особым, т. к., в отличие от общей постановки задачи Коши, в нашем случае начальные условия при 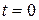 не могут быть заданы произвольно. Для рассматриваемого примера
не могут быть заданы произвольно. Для рассматриваемого примера  , поэтому произвольно
, поэтому произвольно 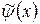 и
и  задать нельзя. Зададим, например,
задать нельзя. Зададим, например,
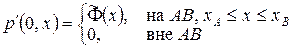
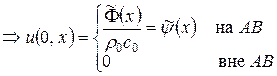
Причем потребуем, чтобы начальные функции  .
.
Т. к.  во всей области
во всей области 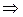 1).
1).  во всей области,
во всей области,
 2).
2). 
Поэтому
 .
.
Это, конечно, следует и из общего решения, напр., для величины возмущения скорости u
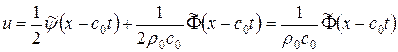 .
.
В этом случае вдоль каждой характеристики  :
:  не только
не только 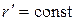 , но и значения
, но и значения 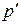 ,
,  также постоянны. Т. е. полученное решение обладает тем свойством, что
также постоянны. Т. е. полученное решение обладает тем свойством, что 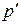 и
и  распространяются вправо со скоростью
распространяются вправо со скоростью 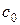 без искажения, т. к. все характеристики
без искажения, т. к. все характеристики  параллельны. Это особое решение называется волной отражения вперед (в линейной постановке прямая волна). В этом случае волна движется вправо со скоростью звука
параллельны. Это особое решение называется волной отражения вперед (в линейной постановке прямая волна). В этом случае волна движется вправо со скоростью звука 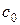 .
.
|
|
|
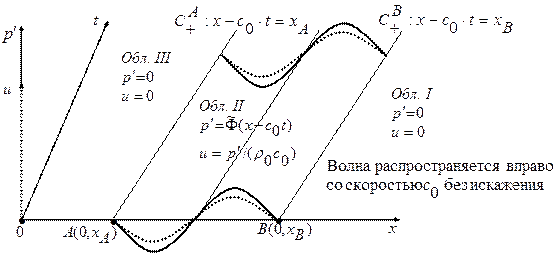
2. Рассмотрим теперь случай, когда во всей области  . В этом случае
. В этом случае  . Рассмотрим задачу Коши при
. Рассмотрим задачу Коши при 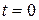 :
:

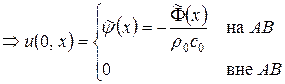
где 
 |
В обл. I и III – состояние покоя. В полосе II между обл. I и III: 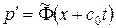 ,
,  . Для этого особого решения (
. Для этого особого решения (  ) вдоль характеристик
) вдоль характеристик  не только
не только 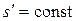 , но и
, но и 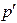 ,
,  также постоянны. Это решение называется простой волной, обращенной назад (в линейной постановке обратная волна). Т. е. полученное решение обладает тем свойством, что
также постоянны. Это решение называется простой волной, обращенной назад (в линейной постановке обратная волна). Т. е. полученное решение обладает тем свойством, что 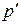 и
и  распространяются влево со скоростью
распространяются влево со скоростью 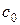 без искажения.
без искажения.
В обоих рассмотренных случаях при 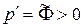 скорость газа
скорость газа  направлена в сторону распространения волны (
направлена в сторону распространения волны ( 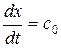 для прямой волны и
для прямой волны и  для обратной волны) и в противоположную сторону, если
для обратной волны) и в противоположную сторону, если 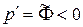 .
.
Волны, когда перемещения среды осуществляются в направлении движения волны или в противоположном направлении движения волны называются продольными.
Замечание. При распространении света (электромагнитных волн) мы имеем дело с поперечными волнами, однако в струне могут иметь место как продольные, так и поперечные волны.
3. Рассмотрим частное решение не особого типа. Пусть при 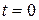 на отрезке AB независимо заданы обе начальные функции
на отрезке AB независимо заданы обе начальные функции  и
и 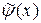 . Предположим, что
. Предположим, что  . Тогда начальные условия в задаче Коши запишутся в виде:
. Тогда начальные условия в задаче Коши запишутся в виде:
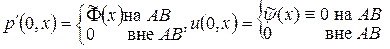 ,
,
где 
Итак, заданы две гладкие функции  и
и 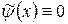 при
при 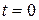 , т. е. в начальный момент времени скорость газа везде равна
, т. е. в начальный момент времени скорость газа везде равна  и задано ненулевое возмущение давления на участке AB. Формально найденное решение дает следующие выражения для
и задано ненулевое возмущение давления на участке AB. Формально найденное решение дает следующие выражения для 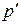 и
и  :
:
 ,
, 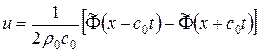 .
.
Более подробно исследуем решение в характеристическом треугольнике (зона 4). При 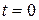 на отрезке AB имеем
на отрезке AB имеем 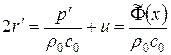 ,
,  .
.

Итак, вдоль 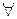 хар-ки
хар-ки 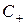 , исходящей из отрезка AB,
, исходящей из отрезка AB,  ,
,
вдоль 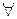 хар-ки
хар-ки  , исходящей из отрезка AB,
, исходящей из отрезка AB, 
вдоль 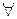 хар-ки
хар-ки 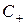 , исходящей из точек вне отрезка AB,
, исходящей из точек вне отрезка AB,  ,
,
вдоль 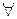 хар-ки
хар-ки  , исходящей из точек вне отрезка AB,
, исходящей из точек вне отрезка AB, 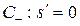 .
.
Поэтому для 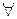 точки
точки  обл. 4 имеем:
обл. 4 имеем:
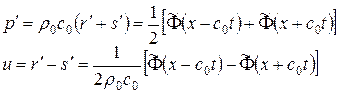

проверим удовлетворяет ли полученное решение при 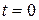 начальным условиям:
начальным условиям:
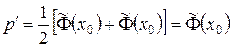 ,
,  .
.
Итак, 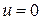 везде при
везде при 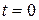 ,
, 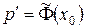 на АВ и
на АВ и  вне AB.
вне AB.
При  начальное возмущение давления распадается на две равные части, каждая из которых имеет ширину AB, а высоту в два раза меньшую, чем начальное возмущение. Каждая из волн
начальное возмущение давления распадается на две равные части, каждая из которых имеет ширину AB, а высоту в два раза меньшую, чем начальное возмущение. Каждая из волн  и
и 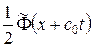 движется без искажения, прямая волна вправо, обратная — влево со скоростями
движется без искажения, прямая волна вправо, обратная — влево со скоростями 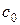 . При
. При  начальное возмущение давления вызывает возмущение скорости
начальное возмущение давления вызывает возмущение скорости  , которое представляет из себя совокупность двух волн каждая из которых имеет ширину AB, а высоту в
, которое представляет из себя совокупность двух волн каждая из которых имеет ширину AB, а высоту в 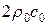 раз меньшую, чем начальное возмущение давления. Причем для прямой волны знак возмущения скорости совпадает со знаком возмущения давления, для обратной – противоположен.
раз меньшую, чем начальное возмущение давления. Причем для прямой волны знак возмущения скорости совпадает со знаком возмущения давления, для обратной – противоположен.
|
|
|
В зоне 4 решение есть сумма прямой и обратной волн. Зоны 1, 3, 6 - области покоя, где  , в зоне 2 (где
, в зоне 2 (где  ) - только прямая волна, в зоне 5 (где
) - только прямая волна, в зоне 5 (где  ) - только обратная волна.
) - только обратная волна.
Итак, в области 4 происходит взаимодействие прямой и обратной волн. Это область не особого решения.
Для величины возмущения скорости в прямой волне (зона 2) имеем 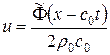 ,
,
для обратной волны (зона 5) имеем  .
.
4. Рассмотрим еще одно частное решение не особого типа. Пусть при 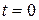 на отрезке AB независимо заданы обе начальные функции
на отрезке AB независимо заданы обе начальные функции  и
и 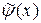 . Предположим теперь, что
. Предположим теперь, что  . Тогда начальные условия в задаче Коши запишутся в виде:
. Тогда начальные условия в задаче Коши запишутся в виде:

 ,
,
где 
Получим аналогичную рассмотренной в пункте 3 задачу. Только теперь величины 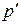 и
и  поменялись местами. Решение задачи дается в виде
поменялись местами. Решение задачи дается в виде
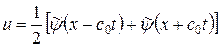 ,
,
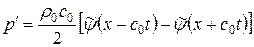 .
.
5. Общий случай.
Задача Коши, начальные данные при 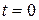 задаются в виде
задаются в виде

 ,
,
где 
Получим общее решение, формулы для которого мы уже выписывали выше. Опять будет в зонах 1, 3, 6 покой, в зонах 2 и 5 — особое решение, а в зоне 4 — решение общего вида. Т. е. качественно мы имеем те же самые результаты, что и в примерах 3 и 4.
Отметим важный результат. Скорость распространения возмущений равна скорости звука 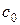 и зависит только от параметров начального состояния и показателя адиабаты Пуассона
и зависит только от параметров начального состояния и показателя адиабаты Пуассона 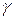 (
(  ) и не зависит от вида функций
) и не зависит от вида функций 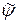 и
и  в начальных данных. Для газа
в начальных данных. Для газа  ; для воздуха
; для воздуха 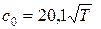 м/с (при
м/с (при 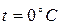
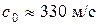 ); для воды
); для воды  .
.
Это отличает акустические волны от, например, поверхностной волны в тяжелой несжимаемой жидкости. Там скорость волны для глубокой жидкости зависит от длины волны. Для воды 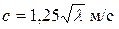 без учета влияния капиллярных сил.
без учета влияния капиллярных сил.
|
|
|


