 |
Общее решение волнового уравнения в сферически-симметричном случае.
|
|
|
|
Общее решение волнового уравнения в сферически-симметричном случае.
Рассмотрим теперь сферический ( 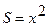 ) случай, т. е. случай волн симметричных относительно начала координат, здесь
) случай, т. е. случай волн симметричных относительно начала координат, здесь  - расстояние от центра (начала координат). В этом случае волновое уравнение (1. 29. 2) примет вид:
- расстояние от центра (начала координат). В этом случае волновое уравнение (1. 29. 2) примет вид:
 , (1. 33. 0)
, (1. 33. 0)
Любопытно, что это уравнение можно преобразовать к уже исследованному виду (1. 30. 0) относительно новой искомой функции  :
:
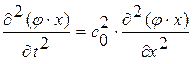 , (1. 33. 1)
, (1. 33. 1)
общее решение которого нам уже известно:
 (1. 33. 2)
(1. 33. 2)
Т. о. формула (1. 33. 2) дает общее решение для сферически-симметричного случая.
Задача Коши для волнового уравнения в случае плоских волн.
Полученные точные общие решения волнового уравнения безусловно имеют огромную важность для дальнейшего изучения свойств волнового уравнения. Следующим этапом является постановка и решение задачи Коши для волнового уравнения (1. 30. 0) в случае плоских волн. Итак, рассматривается уравнение в частных производных второго порядка
 , где
, где  (1. 34. 1)
(1. 34. 1)
с начальными условиями вида
 (1. 34. 2)
(1. 34. 2)
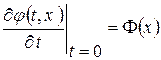 , где
, где 
Наличие в волновом уравнении производной второго порядка по времени обязывает нас ставить начальные условия не только на искомую функцию, но и на первую производную по времени.
Допустим теперь, что решение задачи (1. 34. 1), (1. 34. 2) существует, тогда оно дается формулой  . Определим функции
. Определим функции 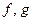 таким образом, чтобы удовлетворялись начальные условия:
таким образом, чтобы удовлетворялись начальные условия:
|
|
|
 , (1. 34. 3)
, (1. 34. 3)
 , (1. 34. 4)
, (1. 34. 4)
Интегрируя второе равенство (1. 34. 4), получаем (  - постоянные):
- постоянные):
 (1. 34. 5)
(1. 34. 5)
Рассматривая (1. 34. 3), (1. 34. 5) как систему 2-х уравнений относительно 2-х неизвестных 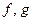 находим:
находим:
 (1. 34. 6)
(1. 34. 6)
Таким образом, мы определили функции 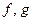 через заданные функции
через заданные функции 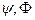 , причем равенства (1. 34. 6) должны иметь место для любого значения аргумента функций
, причем равенства (1. 34. 6) должны иметь место для любого значения аргумента функций 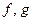 . Подставив в формулу общего решения
. Подставив в формулу общего решения  найденные значения
найденные значения 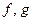 (формулы (1. 34. 6)), получим
(формулы (1. 34. 6)), получим

или
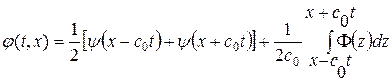 . (1. 35)
. (1. 35)
Впервые это решение задачи Коши для волнового уравнения получил Л. Эйлер в 1748 г.
Сейчас выполним проверку найденного решения в предположении, что 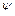 - дважды дифференцируемая функция и
- дважды дифференцируемая функция и  - один раз дифференцируемая функция своего аргумента:
- один раз дифференцируемая функция своего аргумента:
1. Решение удовлетворяет волновому уравнению, так как любая дважды дифференцируемая функция 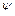 и интеграл от один раз дифференцируемой функции
и интеграл от один раз дифференцируемой функции  от своих аргументов
от своих аргументов 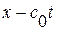 и
и  есть решение волнового уравнения.
есть решение волнового уравнения.
2. Решение удовлетворяет начальным данным задачи Коши. Действительно,
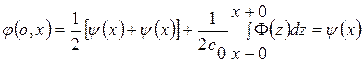 , т. е. первое начальное условие выполнено при всех
, т. е. первое начальное условие выполнено при всех  .
.
Для проверки второго начального условия вспомним формулу вычисления производной от интеграла, зависящего от параметра (правило Лейбница):
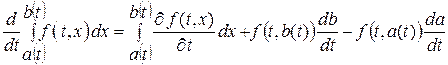 , тогда
, тогда
 Что и требовалось доказать. Отметим, что полученное решение вида (1. 35) называется формулой Д’ Аламбера и доказывает существование решения поставленной задачи Коши. Эта же формула доказывает и единственность решения. Действительно, если бы существовало второе решение задачи (1. 34. 1), (1. 34. 2), то оно представлялось бы формулой (1. 35) и совпадало бы с первым решением.
Что и требовалось доказать. Отметим, что полученное решение вида (1. 35) называется формулой Д’ Аламбера и доказывает существование решения поставленной задачи Коши. Эта же формула доказывает и единственность решения. Действительно, если бы существовало второе решение задачи (1. 34. 1), (1. 34. 2), то оно представлялось бы формулой (1. 35) и совпадало бы с первым решением.
|
|
|
Получим теперь соответствующие найденному решению задачи Коши выражения для возмущений скорости и давления:
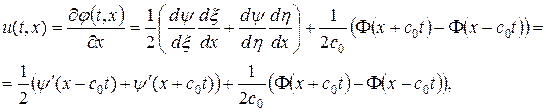 (1. 34. 7)
(1. 34. 7)
 где символом штрих обозначена обыкновенная производная по переменным
где символом штрих обозначена обыкновенная производная по переменным  ,
,  . Найденным выражениям для возмущений скорости и давления соответствуют следующие начальные данные в задаче Коши для искомых функций
. Найденным выражениям для возмущений скорости и давления соответствуют следующие начальные данные в задаче Коши для искомых функций 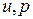 :
:
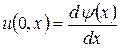 ,
, 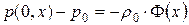 , где
, где 
Физическая интерпретация решения задачи Коши для плоского случая.
Найденная функция 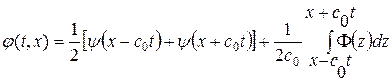 (1. 35)
(1. 35)
представляет процесс распространения начального профиля и начальной скорости возмущения. Если фиксировать 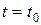 , то функция
, то функция  дает профиль возмущения в момент
дает профиль возмущения в момент  ; фиксируя
; фиксируя 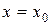 , получим функцию
, получим функцию  , дающую процесс движения точки
, дающую процесс движения точки 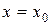 . Предположим, что наблюдатель, находившийся в точке
. Предположим, что наблюдатель, находившийся в точке  в момент
в момент  , движется со скоростью
, движется со скоростью 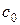 в положительном направлении. Введем систему координат, связанную с наблюдателем, полагая
в положительном направлении. Введем систему координат, связанную с наблюдателем, полагая  . В этой подвижной системе отсчета функция
. В этой подвижной системе отсчета функция  будет определяться формулой
будет определяться формулой 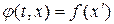 и наблюдатель все время будет видеть тот же профиль, что и в начальный момент. Следовательно, функция
и наблюдатель все время будет видеть тот же профиль, что и в начальный момент. Следовательно, функция 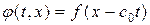 представляет неизменный профиль
представляет неизменный профиль  , перемещающийся вправо по оси
, перемещающийся вправо по оси  со скоростью
со скоростью 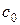 (т. е. бегущую с постоянной скоростью вправо волну неизменной формы). Функция
(т. е. бегущую с постоянной скоростью вправо волну неизменной формы). Функция  представляет, очевидно, волну, распространяющуюся влево со скоростью
представляет, очевидно, волну, распространяющуюся влево со скоростью 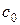 . Т. о., общее решение (1. 35) задачи Коши для бесконечного промежутка
. Т. о., общее решение (1. 35) задачи Коши для бесконечного промежутка 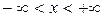 есть суперпозиция двух волн
есть суперпозиция двух волн 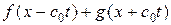 , одна из которых распространяется вправо со скоростью
, одна из которых распространяется вправо со скоростью 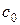 , а вторая - влево с той же скоростью. При этом
, а вторая - влево с той же скоростью. При этом

где 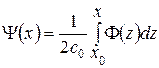 .
.
Для выяснения характера решения (1. 35) удобно воспользоваться фазовой плоскостью  . Прямые
. Прямые 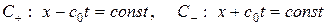 в фазовой плоскости называются характеристиками волнового уравнения. Функции
в фазовой плоскости называются характеристиками волнового уравнения. Функции  сохраняет постоянное значение вдоль характеристики
сохраняет постоянное значение вдоль характеристики  , а функция
, а функция 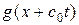 постоянна вдоль характеристики
постоянна вдоль характеристики 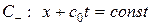 .
.
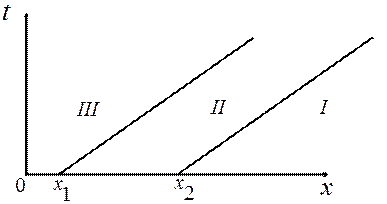 Предположим теперь, что функция
Предположим теперь, что функция  отлична от нуля только в интервале
отлична от нуля только в интервале  и равна нулю вне этого интервала. Проведем характеристики семейства
и равна нулю вне этого интервала. Проведем характеристики семейства  через концы интервала
через концы интервала 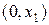 и
и  ; они разбивают полуплоскость
; они разбивают полуплоскость  на три области: I, II, II (Рис. 1. 3).
на три области: I, II, II (Рис. 1. 3).
Рис. 1. 3
Функция  отлична от нуля только в обл. II, где
отлична от нуля только в обл. II, где  , а характеристики
, а характеристики 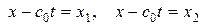 представляют собой задний и передний фронты распространяющейся вправо волны.
представляют собой задний и передний фронты распространяющейся вправо волны.
|
|
|
Рассмотрим теперь некоторую фиксированную точку  и проведем из нее обе характеристики
и проведем из нее обе характеристики 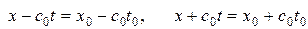 , которые пересекут ось
, которые пересекут ось  в точках
в точках 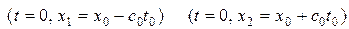 . Значение функции
. Значение функции  в точке
в точке  равно
равно 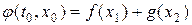 , т. е. определяется значениями функций
, т. е. определяется значениями функций  и
и  в точках
в точках 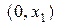 и
и  , являющихся вершинами треугольника MPQ, образованного двумя характеристиками и осью
, являющихся вершинами треугольника MPQ, образованного двумя характеристиками и осью  (Рис. 1. 4).
(Рис. 1. 4).
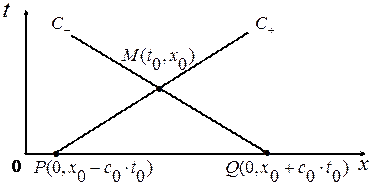
 Рис. 1. 4
Рис. 1. 4
Этот треугольник MPQ называется характеристическим треугольником точки  .
.
Из формулы (1. 35) видно, что величина амплитуды 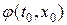 в точке М в момент времени
в точке М в момент времени  зависит только от значений начального возмущения в вершинах Р и Q характеристи-ческого треугольника MPQ и от значений начальной скорости на стороне PQ. Это становится совершенно ясно, если формулу (1. 35) записать в виде:
зависит только от значений начального возмущения в вершинах Р и Q характеристи-ческого треугольника MPQ и от значений начальной скорости на стороне PQ. Это становится совершенно ясно, если формулу (1. 35) записать в виде:

Начальные данные, заданные вне PQ, не оказывают влияния на значение 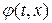 в точке М. Заметим, что, если начальные данные заданы не на всей бесконечной прямой
в точке М. Заметим, что, если начальные данные заданы не на всей бесконечной прямой  , а на некотором отрезке
, а на некотором отрезке 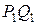 , то они однозначно определяют решение внутри характеристического треугольника, основанием которого является отрезок
, то они однозначно определяют решение внутри характеристического треугольника, основанием которого является отрезок 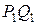 .
.
Перепишем также формулы (1. 34. 7) для значений возмущения скорости и давления:

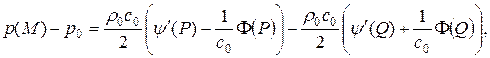
Видно, что значения возмущений скорости и давления в точке М зависят только от начальных данных в точках P и Q.
Два примера: Решение задачи Коши для волнового уравнения (1. 35) можно также представить в виде в суммы функций:
 , (1. 36)
, (1. 36)
где  , (1. 37)
, (1. 37)
где  , (1. 38)
, (1. 38)
тогда, если начальная скорость возмущения равна нулю ( 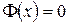 ), то амплитуда возмущения
), то амплитуда возмущения  есть сумма левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией
есть сумма левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией  , равной половине начального возмущения. Если же наоборот
, равной половине начального возмущения. Если же наоборот 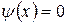 и
и  , то решение
, то решение 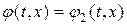 представляет возмущение, создаваемое начальной скоростью.
представляет возмущение, создаваемое начальной скоростью.
Пример 1: Рассмотрим распространение начального возмущения 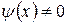 и
и 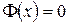 , заданного на отрезке
, заданного на отрезке  , при помощи представления решения в виде (1. 36). Для этого проведем характеристики обоих семейств через точки
, при помощи представления решения в виде (1. 36). Для этого проведем характеристики обоих семейств через точки  и
и 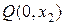 ; они разобьют верхнюю полуплоскость на шесть областей (Рис. 1. 5). Величина возмущения для наших начальных данных дается формулой (1. 37), т. е.
; они разобьют верхнюю полуплоскость на шесть областей (Рис. 1. 5). Величина возмущения для наших начальных данных дается формулой (1. 37), т. е.  в любой точке
в любой точке  . Поэтому в областях I, III, V возмущение равно нулю, т. к. боковые стороны характеристического треугольника для любой точки из этих областей не пересекаются с отрезком PQ, на котором задано начальное возмущение. В области II решением является правая волна
. Поэтому в областях I, III, V возмущение равно нулю, т. к. боковые стороны характеристического треугольника для любой точки из этих областей не пересекаются с отрезком PQ, на котором задано начальное возмущение. В области II решением является правая волна
|
|
|

|
|
|


