 |
Задача Коши для волнового уравнения на полуограниченной прямой. Метод продолжений.
|
|
|
|
Рис. 1. 5
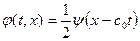, в области IV – левая волна 
, а в области VI решение есть сумма левой и правой волн. Область, образованная областями II+IV+VI, называется областью влияния начальных данных, заданных на отрезке PQ. (Схематически для случая начального возмущения в форме треугольника последовательные положения профиля волны представлены на Рис. 1. 6. 1)
В случае задания на отрезке PQ ненулевого значения начальной скорости возмущения (т. е.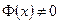 
) область влияния включала бы в себя области II+IV+VI и плюс область III.
Рис. 1. 6. 1
Пример 2: Рассмотрим распространение возмущения со следующими начальными данными: начальное возмущение отсутствует ( 
), а начальная скорость 
отлична от нуля только на отрезке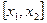 
, где она принимает постоянное значение 
:
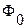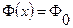при 
, 
при 
и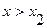 
. В этом случае решением является функция 
из (1. 36)-(1. 38). Вычислим функцию 
, положив при этом 
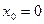(график функции дан на Рис. 1. 6. 2):
Решение есть разность правой и левой волн с профилем . Последовательные положения этих волн в моменты времени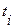 
изображены на Рис. 1. 6. 3. Изначально нулевой профиль возмущения с ростом времени 
приобретает форму трапеции, расширяющейся равномерно с течением времени. Заметим, что, если отлична от постоянной на отрезке 
, то изменится только профиль .
Для выяснения характера полученного решения воспользуемся фазовой плоскостью 
.
Напишем выражения для 
в различн. областях фазовой пл-ти (Рис. 1. 5).
В обл. I. ( 
): 
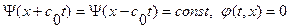
В обл. V. (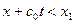 
): 
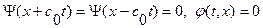
В обл. III. ( 
): 
В обл. II. ( 
): 
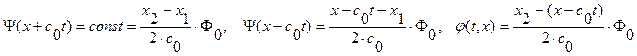
В обл. IV. ( 
): 
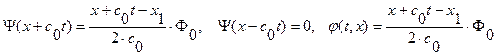
В обл. VI. ( 
): 
Понятие устойчивости решения.
|
|
|
Найденное нами решение Д’ Аламбера (1. 35) задачи Коши для волнового уравнения (1. 34. 1) однозначно определено начальными условиями (1. 34. 2). Докажем теперь, что это решение меняется непрерывно при непрерывном изменении начальных условий.
Утверждение: Каков бы ни был промежуток времени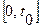 
и какова бы ни была степень точности 
, найдется такое 
, что всякие два решения волнового уравнения (1. 34. 1) 
и 
в течение промежутка времени 
будут различаться меньше чем на :
,
если только начальные значения
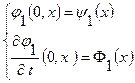и 
отличаются друг от друга меньше, чем на 
:
.
Доказательство:
Функции и связаны со своими начальными значениями формулой Д’Аламбера (1. 35), поэтому справедлива оценка
из этой оценки получаем
, и далее выбор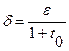 
доказывает наше утверждение.
Если решение математической задачи непрерывно зависит от дополнительных условий (от начальных, граничных данных и от правой части уравнения – т. е. от исходных данных задачи), то говорят, что задача устойчива.
Говорят, что математическая задача поставлена корректно, если:
- решение задачи существует,
- решение задачи единственно,
- решение задачи непрерывно зависит от исходных данных (устойчиво).
Отметим одно важное обстоятельство. Очевидно, что функция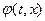 
, определяемая формулой (1. 35), может быть решением волнового уравнения только в том случае, если функция дифференцируема, а функция 
дифференцируема дважды. Из сказанного ясно, что функции, изображенные на Рис. 1. 6, не могут являться решением волнового уравнения, т. к. они не всюду дважды дифференцируемы. Однако если немного изменить начальные условия (сгладить), заменив их дифференцируемыми функциями и , то этим начальным функциям уже будет соответствовать решение волнового уравнения (1. 34. 1). Кроме того заметим, что при доказательстве утверждения настоящего пункта мы фактически доказали, что функции, определяемые формулой (1. 35), непрерывно зависят от начальных функций и (независимо от того, дифференцируемы эти функции или нет). Т. о., если некоторым функциям 
и не соответствует решение волнового уравнения, удовл. нач. усл. (1. 34. 2), то функция, определяемая формулой (1. 35), является пределом решений волнового уравнения с немного сглаженными начальными условиями. Полученные таким предельным переходом функции называются обобщенными решениями, понятие которых было введено С. Л. Соболевым.
|
|
|
Задача Коши для волнового уравнения на полуограниченной прямой. Метод продолжений.
Рассмотрим задачу Коши о распространении волн на полуограниченной прямой ( 
). Эта задача имеет особенно важное значение при изучении процессов отражения волн от границы рассматриваемой области поиска решения.
Постановка задачи:
Найти решение волнового уравнения
, где 
(1. 40. 1)
с начальными условиями
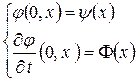, где 
(1. 40. 2)
и с граничным условием
(или 
), где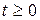 
(1. 40. 3)
Рассмотрим сначала случай однородного граничного условия, т. е.
(или 
), где 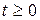, (1. 40. 4)
что отвечает задаче о распространении начального возмущения с закрепленным концом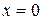 
( или свободным концом ).
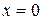Для построения решения докажем 2 свойства решений волнового уравнения для случая бесконечной прямой:
1. Если начальные данные в задаче о распространении возмущений на неограниченной прямой (задача (1. 34. 1), (1. 34. 2)) являются нечетными функциями относительно некоторой точки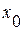 
, то соответствующее решение в этой точке 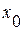равно нулю.
2. Если начальные данные в задаче о распространении возмущений на неограниченной прямой (задача (1. 34. 1), (1. 34. 2)) являются четными функциями относительно некоторой точки 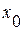, то производная по 
соответствующего решения в этой точке 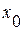равна нулю.
Док-во св-ва 1: Примем 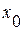за начало координат, 
. Тогда условия нечетности нач. данных примут вид: 
.
Решение (1. 35) при 
равно
т. к. оба слагаемых равны нулю в виду нечетности функций 
и симметрии интервалов.
|
|
|
Док-во св-ва 2: Примем 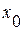за начало координат, . Тогда условия четности нач. данных примут вид: 
. Заметим также, что производная четной функции является нечетной функцией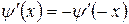 
. Тогда из формулы (1. 35)
т. к. первое слагаемое равно нулю в силу нечетности производной 
, а второе - в виду четности 
.
Приведенное выше доказательство фактически опирается на формулу Д’ Аламбера (1. 35) и не связано с двукратной дифференцируемостью функции 
. Тем самым доказано, что свойство 1 верно для любых функций, представимых формулой Д’ Аламбера, а свойство 2 – для функций того же вида с дифференцируемой функцией 
, т. е. для обобщенных решений задачи (1. 34. 1), (1. 34. 2).
Указанные свойства помогут теперь решить первую краевую задачу:
Найти решение волнового уравнения
, где ,
удовлетворяющее начальным условиям
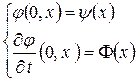, где
и граничному условию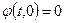 
, где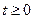 
.
Рассмотрим функции 
и 
, являющиеся нечетным продолжением функций 
и на отрицательную часть оси абсцисс.
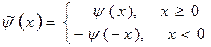
Рассмотрим функцию
она определена для всех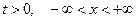 
, т. е. на всей прямой. В силу св-ва 1 имеем
. Кроме того, эта функция удовлетворяет при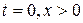 
следующим начальным условиям: 
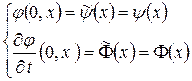. Рассматривая теперь полученную функцию 
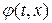только для значений 
, мы получим функцию, удовлетворяющую всем условиям задачи.
Возвращаясь к прежним функциям, мы получим окончательный вид решения:
(1. 41)
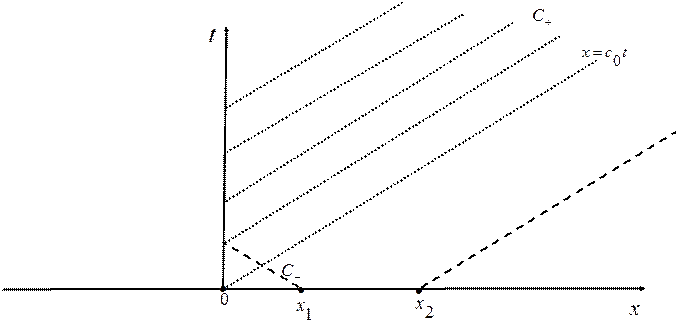Из (1. 41) видно, что в области 
влияние граничных условий не сказывается, и выражение для 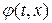совпадает с решением для случая бесконечной прямой. На Рис. 1. 7 представлены для сравнения области влияния начальных и граничных данных.
|
|
|
