 |
Задача об отражении акустической ударной волны от абсолютно твердой (жесткой) стенки для случая плоских волн.
|
|
|
|
Рассмотрим задачу отражения акустической ударной волны от жесткой стенки для случая плоских волн ( 
). Пусть по трубе, заполненной покоящимся газом с параметрами 
и закрытой справа (в сечении 
) жесткой стенкой, распространяется слева направо с постоянной скоростью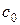 
ударная волна (У. В. ) заданной интенсивности (т. е. заданы значения 
за У. В. ). В момент времени 
У. В. достигает жесткой стенки. Требуется рассчитать движение и параметры газа при 
. Эта задача с граничным условием, т. к. наличие жесткой стенки означает, что на ней должно быть выполнено граничное условие непротекания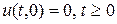 
. На нижеследующих рисунках 3. 11, 3. 12 представлена картина отражения У. В. в физической и фазовой плоскостях.
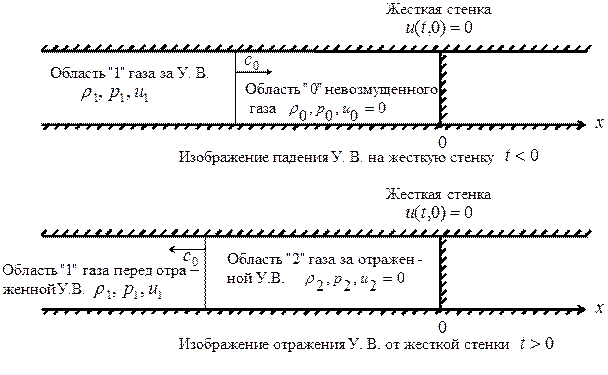
Рис. 3. 11 Картина отражения У. В. от жесткой стенки в физической плоскости
 |
Рис. 3. 12 Картина отражения У. В. от жесткой стенки в фазовой плоскости
Представленная на Рис. 3. 11, 3. 12 графическая интерпретация отражения У. В. от жесткой стенки стала возможной благодаря анализу возможных состояний нашей системы на плоскости 
- диаграмм (Рис. 3. 13).
Рис. 3. 13. - диаграмм падения-отражения У. В. от жесткой стенки
Как было показано ранее, прямая 
, проходящая через точку с координатами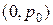 
в плоскости , отображает множество возможных состояний газа за правой У. В. Аналогом этой прямой, выражающей условие постоянства левого инварианта Римана 
вдоль характеристики 
когда та пересекает правую У. В. (характеристика 
), в плоскости переменных служит характеристика в фазовой плоскости переменных 
. В нашем случае состояние за падающей У. В. известно по условиям задачи – это точка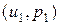 
на диаграмме. Множество возможных состояний после отражения У. В. от жесткой стенки лежит на прямой 
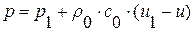, проходящей через точку с координатами 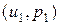и выражающей условие постоянства правого инварианта Римана 
вдоль характеристики , когда та пересекает траекторию левой У. В. (характеристика ). Значение величины давления 
определяется как точка пересечения прямой 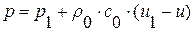с осью 
, т. к. мы должны удовлетворить граничному условию непротекания на жесткой стенке 
. Вычислим искомые значения параметров задачи.
|
|
|
Для падающей ударной волны, распространяющейся вправо (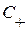 
: 
):
, т. к. 
Для отраженной ударной волны, распространяющейся влево ( 
: 
):
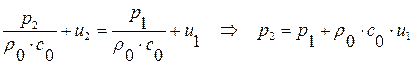, т. к. 
Таким образом, по известной из условий задачи величине скорости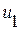 
(или давления 
) за падающей У. В. могут быть найдены все остальные параметры задачи отражения У. В. от стенки.
Одной из важных особенностей отражения У. В. от жесткой стенки является усиление действия падающей У. В. после отражения, характеризуемое коэффициентом усиления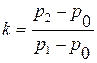 
. Как видно из формулы, коэффициент усиления характеризует отношение избыточного давления 
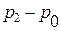после отражения У. В. к избыточному давлению 
в падающей У. В. Для рассматриваемого нами акустического случая отражения У. В. от жесткой стенки 
, т. е. коэффициент усиления для слабых акустических волн постоянен и равен 2 и не зависит от интенсивности падающей волны. Т. е. при отражении даже слабой акустической волны избыточное давление удваивается. Отметим, что в общей нелинейной постановке для нашей задачи максимальный коэффициент усиления для отраженной волны 
при условии, что интенсивность падающей У. В. 
. Для воздуха (показатель адиабаты Пуассона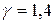 
) максимальное возрастание избыточного давления после отражения по отношению к избыточному давлению в падающей волне равно 8.
|
|
|
