 |
Некоторые свойства одномерных плоских, сферических и цилиндрических волн.
|
|
|
|
Некоторые свойства одномерных плоских, сферических и цилиндрических волн.
Волновое уравнение для нахождения потенциала  в одномерном случае:
в одномерном случае:
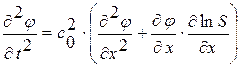 , (1. 29. 2)
, (1. 29. 2)
Уравнение (1. 29. 2) для случаев плоских ( 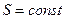 ) и сферических волн (
) и сферических волн ( 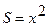 ) интегрируется в конечном виде, т. е. может быть найдено его общее решение.
) интегрируется в конечном виде, т. е. может быть найдено его общее решение.
Распространение сигнала от точечного источника для случая плоских волн.
Рассмотрим случай плоских ( 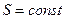 ) волн. Тогда волновое уравнение (1. 29. 2) примет вид:
) волн. Тогда волновое уравнение (1. 29. 2) примет вид:  , (3. 1)
, (3. 1)
Введем новые независимые переменные, получившие название характеристических переменных,  ,
,  . (3. 2)
. (3. 2)
Тогда волновое уравнение примет вид 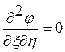 , интегрирование которого дает
, интегрирование которого дает
 (3. 3)
(3. 3)
Здесь  и
и 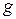 - произвольные дважды дифференцируемые функции своих аргументов.
- произвольные дважды дифференцируемые функции своих аргументов.
Произвольные функции  и
и 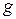 определяются по заданным начальным и/или граничным условиям.
определяются по заданным начальным и/или граничным условиям.
Рассмотрим задачу о распространении сигнала из точки  в область
в область  с граничным условием вида
с граничным условием вида 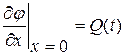 (3. 4)
(3. 4)
(выбор в граничном условии функции  вместо
вместо 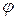 связан с удобством сравнения решений в задачах об источнике в плоском, цилиндрическом и сферическом случаях).
связан с удобством сравнения решений в задачах об источнике в плоском, цилиндрическом и сферическом случаях).
Решение имеет вид  (3. 5)
(3. 5)
Из формулы (3. 5) видно, что возмущение ограничено во времени интервалом

Т. е., если принять, что источник в точке  издавал сигнал в течение времени
издавал сигнал в течение времени  , то первый сигнал к наблюдателю прибывает с волновым фронтом, покинувшим источник при
, то первый сигнал к наблюдателю прибывает с волновым фронтом, покинувшим источник при  , а прекращается возмущение вместе с сигналом, покинувшим источник в последний момент времени
, а прекращается возмущение вместе с сигналом, покинувшим источник в последний момент времени 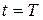 .
.
|
|
|
Два примера задач о распаде произвольного разрыва для случая плоских волн.
Рассмотрим два примера задач, содержащих сильный разрыв в начальных данных, для случая плоских волн (  ).
).
Первая задача. Зададим начальные условия для задачи Коши в виде:
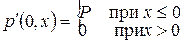 , где
, где 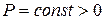 ,
, 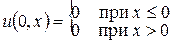 .
.
Данные начальные условия моделируют покоящийся газ, разделенный на две части перегородкой (разрывом в начальных данных), в левой части задано возмущение давления 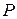 . При
. При 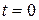 перегородка убирается. Задача найти решение при
перегородка убирается. Задача найти решение при  .
.
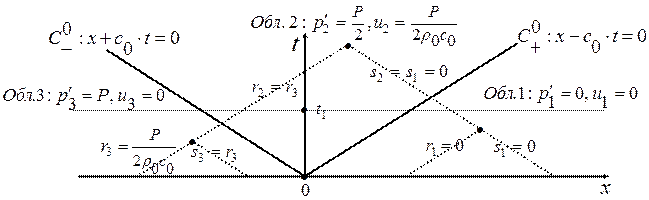 | |||
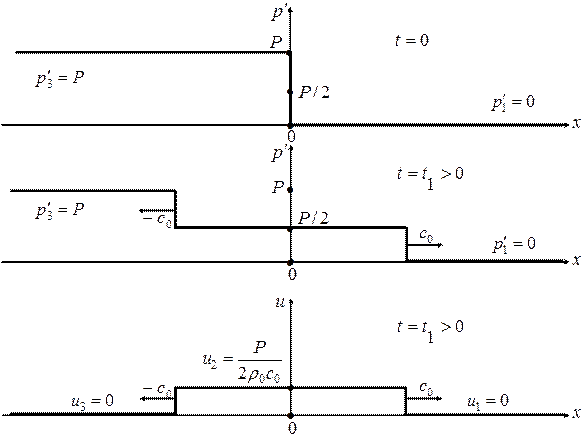 | |||
Для построения решения заметим, что вдоль  выполнено
выполнено  ,
,
вдоль  выполнено
выполнено 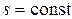 ,
,
где 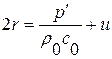 ,
, 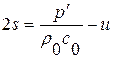 и, след.,
и, след., 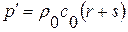 ,
,  .
.
Тогда в области 1: 
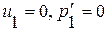 ,
,
в области 3: 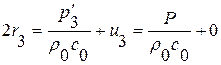
 ,
, 
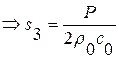 , тогда
, тогда  ,
, 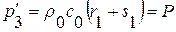 . Как видно из решения области 3 и 1 ничего не знают о том, что в начале координат при
. Как видно из решения области 3 и 1 ничего не знают о том, что в начале координат при  имел место разрыв начальных данных.
имел место разрыв начальных данных.
Рассмотрим область 2. Так как для  :
: 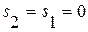 , а для
, а для 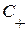 :
:  , то
, то 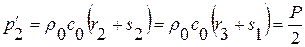 ,
, 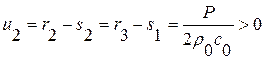 .
.
Интересный факт: чисто формально получается, что при очень большом  следует
следует  , т. е. предположение о линейности есть сильное и неправильное при
, т. е. предположение о линейности есть сильное и неправильное при  ? В нелинейной постановке: для газа с показателем адиабаты
? В нелинейной постановке: для газа с показателем адиабаты 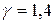 имеем, что при
имеем, что при 
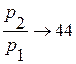 . Для жидкости предположение о линейности хорошо работает при
. Для жидкости предположение о линейности хорошо работает при 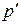 до 500 атм. и удовлетворительно до 1000 атм..
до 500 атм. и удовлетворительно до 1000 атм..
Итак, в линейной постановке вправо по газу с нулевым возмущением давления побежит ударная волна сжатия 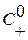 с амплитудой давления
с амплитудой давления  , влево по газу с положительным возмущением давления
, влево по газу с положительным возмущением давления 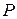 побежит ударная волна разрежения
побежит ударная волна разрежения 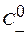 с амплитудой
с амплитудой 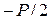 .
.
Вторая задача. Зададим начальные условия для задачи Коши в виде:
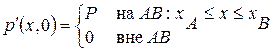 ,
, 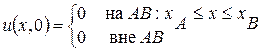 .
.
Данные начальные условия моделируют покоящийся газ, разделенный на три части двумя перегородками (разрывы в начальных данных в точках А и В), в центральной части (отрезок АВ) задано возмущение давления 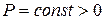 . При
. При 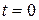 перегородки убираются. Задача найти решение при
перегородки убираются. Задача найти решение при  .
.
Для построения решения заметим, что вдоль  выполнено
выполнено  ,
,
|
|
|
вдоль  выполнено
выполнено 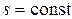 ,
,
где 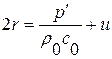 ,
, 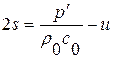 и, след.,
и, след., 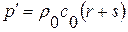 ,
,  .
.
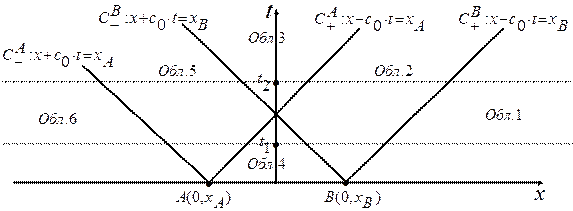 | |||
 | |||
Тогда в областях 1, 2, 3 будет выполнено: 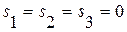 ,
, 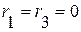 ;
;
в областях 6, 5, 3 будет выполнено:  ,
,  ;
;
Поэтому в областях 1, 3, 6: 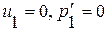 ;
;  ;
;  ;
;
В обл. 4:  ,
, 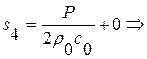
 и
и 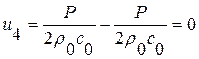 ;
;
В обл. 2: 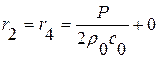 ,
, 
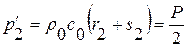 и
и  ;
;
В обл. 5: 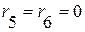 ,
, 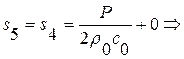
 и
и  .
.
Итак, также, как и в случае гладких решений класса  , начальное давление сразу же распадается на две равные половинки
, начальное давление сразу же распадается на две равные половинки  . Одна половина движется вправо со скоростью
. Одна половина движется вправо со скоростью  , другая — влево со скоростью
, другая — влево со скоростью 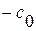 . Однако, как и в первой задаче, каждая точка разрыва порождает пару волн. В ударных волнах сжатия
. Однако, как и в первой задаче, каждая точка разрыва порождает пару волн. В ударных волнах сжатия  и
и  давление в газе повышается на
давление в газе повышается на  и газ вовлекается в движение вслед за волной со скоростью
и газ вовлекается в движение вслед за волной со скоростью 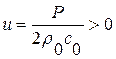 для прямой волны и
для прямой волны и 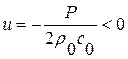 для обратной волны. Через время
для обратной волны. Через время 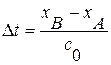 после прохождения ударных волнах сжатия
после прохождения ударных волнах сжатия  и
и  частицы газа испытывают воздействие ударных волнах разрежения
частицы газа испытывают воздействие ударных волнах разрежения  и
и  , после которых давление в газе скачком понижается на
, после которых давление в газе скачком понижается на  до нуля и скорость газа становится равной нулю, т. е. газ возвращается (обл. 3) в исходное невозмущенное состояние (обл. 1, 6).
до нуля и скорость газа становится равной нулю, т. е. газ возвращается (обл. 3) в исходное невозмущенное состояние (обл. 1, 6).
Рассмотренные в качестве примеров задачи имеют большое прикладное и теоретическое значения. Заметим, что если ось 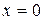 заменить абсолютно твердой стенкой, т. е. задать на ней условие
заменить абсолютно твердой стенкой, т. е. задать на ней условие  , то можно получить новое семейство задач.
, то можно получить новое семейство задач.
|
|
|


