 |
Задача о поршне в акустической постановке для случая плоских волн.
|
|
|
|
Задача о поршне в акустической постановке для случая плоских волн.
Рассмотрим задачу о поршне, вдвигаемом в трубу или выдвигаемом из трубы постоянного поперечного сечения( 
), заполненной газом. Решение будем строить в рамках рассматриваемого линейного приближения (акустической постановки). Итак, пусть в трубе, заполненной покоящимся газом с параметрами 
, в момент времени 
из положения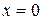 
начинает двигаться поршень с постоянной скоростью 
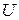. Требуется рассчитать движение и параметры газа при 
. Эта задача с граничным условием, т. к. наличие движущегося поршня означает, что на нем должно быть выполнено граничное условие непротекания, т. е. скорость частиц газа, прилегающих к поршню, должна равняться скорости поршня 
. На нижеследующих рисунках 3. 14, 3. 15 представлена картина течения в физической и фазовой плоскостях для случая вдвигаемого (Рис. 3. 14) и выдвигаемого(Рис. 3. 15) поршня.
Рис. 3. 14 Картина течения в физической и фазовой плоскостях для случая вдвигаемого поршня
Рис. 3. 15 Картина течения в физической и фазовой плоскостях для случая выдвигаемого поршня
Представленная на Рис. 3. 14, 3. 15 графическая интерпретация течений в физической и фазовой плоскостях стала возможной благодаря анализу возможных состояний нашей системы на плоскости 
- диаграмм (Рис. 3. 16).
 |
Рис. 3. 16. - диаграмма в задаче о поршне
Как было показано ранее, аналогом 
характеристики в фазовой плоскости с уравнением 
в рассматриваемой нами плоскости переменных является прямая 
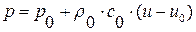, проходящая через точку с координатами 
. Эта прямая – суть условие постоянства левого инварианта Римана 
при пересечении характеристики по направлению вдоль характеристики 
- отображает множество возможных состояний газа за правой У. В. В нашей задаче среда по которой могут распространяться возмущения (волны), инициируемые движущимся поршнем, расположена справа от поршня. Поэтому множество возможных состояний “1”, в которые может перейти газ из состояния “0”, будет располагаться на прямой постоянных значений левого инварианта Римана :
|
|
|
, т. к. 
Значение скорости 
в виду наличия левого граничного условия в задаче – условия непротекания на поверхности поршня – позволяет найти величину давления за волной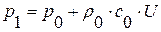 
. По найденному значению давления найдем величину плотности 
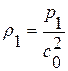из уравнения состояния. Значение 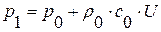в случае вдвигающегося поршня 
будет больше начального 
, т. е. вправо побежит У. В. сжатия, в случае выдвигающегося поршня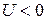 
величина 
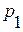будет меньше , т. е. вправо побежит У. В. разрежения. Заметим также, что при величине 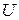равной 
значение 
и при дальнейшем увеличении абсолютной величины скорости 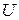при выдвижении поршня газ “оторвется от поршня”, т. е. вблизи поршня образуется область вакуума.
Распространение сигнала от точечного источника для случая сферических волн.
Рассмотрим теперь сферический ( 
) случай, т. е. случай волн симметричных относительно начала координат, здесь 
- расстояние от центра (начала координат). В этом случае волновое уравнение (1. 29. 2) примет вид:
, (3. 20)
Это уравнение можно преобразовать к уже исследованному виду (3. 1) относительно новой искомой функции 
:
, (3. 21)
общее решение которого нам уже известно:
(3. 22)
Рассмотрим случай источника, генерирующего только уходящие волны, тогда решение принимает вид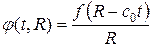 
, где функция 
определяется свойствами источника. Обычно их удобно задавать в виде
|
|
|
(3. 23)
Из (3. 23) в предположении ограниченности 
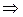
, поэтому потенциал 
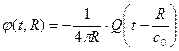(3. 24)
Физический смысл: 
- объемный расход жидкости,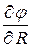 
- радиальная скорость.
Из формулы (3. 24), как и в плоском случае (3. 5) видно, что возмущение ограничено во времени интервалом
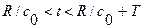
Т. е., если принять, что источник издавал сигнал в течение промежутка времени 
, то первый сигнал к наблюдателю прибывает с волновым фронтом, покинувшим источник при , а прекращается возмущение вместе с сигналом, покинувшим источник в последний момент времени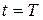 
.
|
|
|
