 |
Распространение сигнала от источника для случая цилидрических волн.
|
|
|
|
Распространение сигнала от источника для случая цилидрических волн.
Рассмотрим теперь цидиндрический (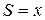 
) случай, т. е. случай волн симметричных относительно оси координат 
, здесь 
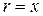- расстояние от оси симметрии (Рис 4. 1).
Рис. 4. 1
В этом случае волновое уравнение (1. 29. 2) примет вид:
, (4. 1)
Построение решения уравнения (4. 1) будет основываться на обобщении найденного выше (формула (3. 24)) решения для сферически-симметричного случая для источника, генерирующего только уходящие волны. Для этого положим, что источники распределены равномерно вдоль оси с плотностью 
на единицу длины (Рис. 4. 1). В этом случае полное возмущение, создаваемое таким распределением, является функцией только от расстояния 
до оси и от времени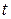 
. Таким образом, мы получаем цилиндрическую волну, генерируемую линейным источником. Полное возмущение, следуя (3. 24), тогда будет равно
, где 
(4. 2)
Полученное решение (4. 2) может быть записано в различных формах. Так, подставив в интеграл 
, получим
(4. 3)
Применив другую подстановку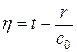 
, 
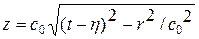, получим
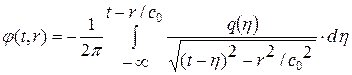(4. 4)
Формула (4. 3) удобнее для вычисления производных от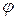 
и, следовательно, для непосредственной проверки справедливости волнового уравнения для полученного решения в форме (4. 3). Действительно, после вычисления соотв. производных и подстановки в (4. 1) получим, что
Последний предел равен нулю, если, например, 
, или, например, если 
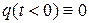, что завершает проверку.
|
|
|
Из формулы (4. 4) в отличие от плоского случая (3. 5) или сферического (3. 24) не следует, что возмущение от источника, издававшего сигнал в течение промежутка времени Т, ограничено во времени интервалом
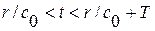
Т. е., если принять, что источник издавал сигнал в течение промежутка времени 
, то в цилиндрическом случае первый сигнал к наблюдателю прибывает с волновым фронтом, покинувшим источник при 
, но действие возмущения продолжается и после момента времени 
. Действительно, из представления решения (4. 4) имеем:
, где 
.
Тогда для фиксированного получим оценку
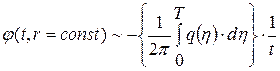при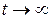 
, т. е. возмущение будет стремится к нулю только асимптотически при .
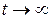Это важное различие между нечетным и четным числом измерений было замечено Адамаром. Можно сказать, что иметь дело с нечетным числом измерений проще, чем с четным, поэтому цилиндрическое волновое решение было выведено из сферического волнового решения. Другим способом получить указанное решение можно было методом спуска из общего решения Пуассона для трехмерного случая.
Задача о распаде разрыва в акустической постановке для сферического случая.
Рассмотрим шар радиуса 
. Пусть давление в газе внутри шара равно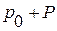 
, снаружи шара давление равно 
. Газ первоначально всюду покоится. В момент времени 
оболочка шара разрушается. Тогда согласно определениям скорости и давления через потенциал 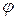начальные условия в нашей задаче для волнового уравнения примут вид:
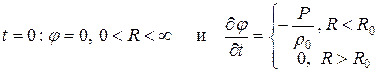, (3. 25)
т. е. решение 
при 
должно удовлетворять условиям:
(3. 26)
Условия (3. 26) определяют функции 
для положительных значений их аргументов. Однако в решение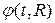 
- (3. 22) входят значения функции 
и для отрицательных значений аргумента. Недостающее условие связано с поведением решения в начале координат и связано с требованием отсутствия источника в начале координат, т. е.
|
|
|
,
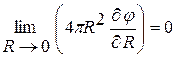следовательно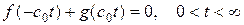 
(3. 27)
Как видно, условие (3. 27) определяет функцию для отрицательных значений аргумента по известным значениям функции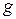 
для положительных значений аргумента. Решая совместно уравнения (3. 26) и (3. 27), находим выражения для функций :
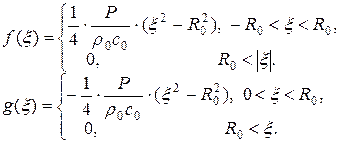
Поэтому, формула для возмущения давления принимает вид:
, где функции 
равны
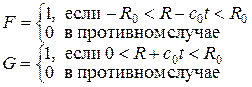
Картина характеристик и изменение давления со временем изображены на Рис. 3. 1. Как видно, для точек 
давление скачком возрастает на величину 
в момент времени 
, затем избыточное давление линейно убывает со временем, достигая величины 
в момент времени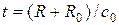 
, а потом скачком возвращается к нулю. Даже при 
скачок на фронте волны равен только 
, остальная часть от полного скачка 
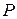поглощается идущей к центру волной разрежения.
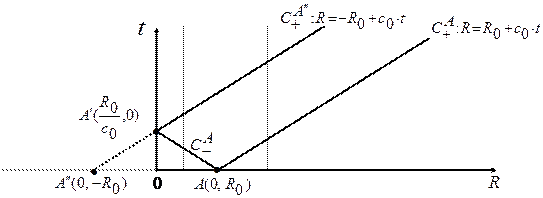
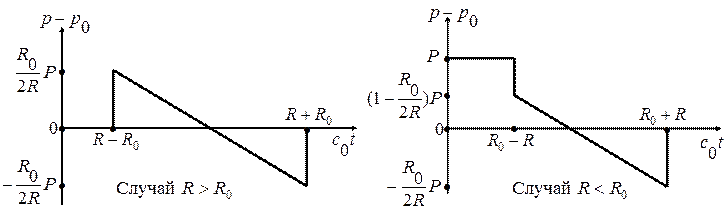Рис. 3. 1
Для внутренних точек 
скачкообразное изменение давления, уменьшающее исходное значение 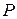до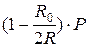 
, происходит в момент времени 
, затем избыточное давление линейно убывает со временем, достигая величины в момент времени 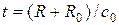, а потом скачком возвращается к нулю.
Итак, при распаде разрыва на сфере радиуса 
одновременно возникают две ударные волны. Ударная волна сжатия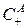 
распространяется от центра по газу с давлением 
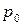с постоянной скоростью 
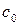, ее интенсивность падает по мере удаления от поверхности радиуса 
по закону 
по достижении поверхности радиуса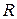 
. Ударная волна разрежения 
распространяется к центру по газу с давлением 
с постоянной скоростью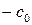 
, ее интенсивность увеличивается по мере схождения к центру по закону 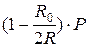по достижении поверхности радиуса 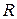. Далее ударная волна разрежения схлопывается в центре 
и отражается от центра в виде ударной волны сжатия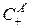 
. Заметим, что в центре изменения бесконечно велики, но весь процесс занимает бесконечно малый интервал времени. Возникшая ударная волна сжатия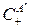 
движется от центра с постоянной скоростью 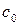и переменной интенсивностью 
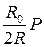поднимая величину давления в расширяющемся газе до величины .
|
|
|
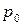