 |
Практическая работа №6 «Параллельность прямых и плоскостей»
|
|
|
|
Практическая работа №6 «Параллельность прямых и плоскостей»
Задание:
1. Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1, М1. Найдите длину отрезка ММ1, если отрезок АВ не пересекает плоскость и если: АА1= 6 м, ВВ1= 7 м.
2. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пересекающие плоскость в точках В1 и С1. Найдите длину отрезка ВВ1, если: СС1=10см, АС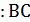 
=3: 2.
3. Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А1, а сторону ВС – в точке В1. Найти длину отрезка А1В1, если:
АВ=10см, АА1: АС=2: 5.
4. Плоскости α и β параллельны между собой. Из точки М, которая не принадлежит этим плоскостям и не находится между ними, проведены два луча. Один из них пересекает эти плоскости α и β в точках А1 и В1, а другой –в точках А2 и В2 соответственно. Найдите длину отрезка В1В2, если он на 4 см больше отрезка А1А2, МВ1 = 9см, А1В1=6см.
5. . Даны две параллельные плоскости. Через точки А и В одной из этих параллельных плоскостей проведены параллельные прямые, пересекающие вторую плоскость в точках А1 и В1. Чему равен отрезок А1В1, если: АВ = m.
Контрольные вопросы:
1. Какие две прямые в пространстве называются параллельными?
2. Сформулируйте признак параллельности прямых в пространстве.
3. Какие прямая и плоскость называются параллельными?
4. Сформулируйте признак параллельности прямой и плоскости.
5. Какие две плоскости называются параллельными?
6. Сформулируйте признак параллельности плоскостей.
7. Сделайте геометрическую иллюстрацию свойств параллельности плоскостей в пространстве и сформулируйте их.
|
|
|
|
Критерии оценивания | ||
|
Процент Результативности (правильных ответов) |
Качественная оценка индивидуальных образовательных достижений | |
| Балл (отметка) | Вербальный аналог | |
| 100-85 | отлично | |
| 84-70 | хорошо | |
| 69-50 | удовлетворительно | |
| Менее 49 | не удовлетворительно | |
Контрольная работа № 3.
I вариант
Решите задачу.
На рисунке изображена правильная треугольная пирамида SABC. Точки K, N, M – середины ребер SA, SB, AB соответственно. Точка F делит ребро SC в отношении 1: 3, считая от вершины S. SO – перпендикуляр к плоскости ABC.
1) Укажите:
а) прямую, параллельную плоскости АВС, ответ обоснуйте;
б) прямые, скрещивающиеся с прямой АВ;
в) угол наклона ребра SC к плоскости ABC;
г) линейный угол двугранного угла SABC.
2) Постройте:
а) точку пересечения прямой FN с плоскостью ABC;
б) прямую в плоскости SBC, проходящую через точку N, параллельно плоскости АВС;
в) угол наклона ребра SB к плоскости ABC;
г) из точки О и S перпендикуляры к прямой ВС;
д) из точки F прямую, параллельную прямой SO.
Обоснуйте построения.
II вариант
Решите задачу.
На рисунке изображена пирамида SABCD, у которой основание ABCD – прямоугольник, а ребро SA расположено перпендикулярно основанию. Четырехугольник KLMN – сечение пирамиды плоскостью. Точки N и K являются серединами ребер SA и SB соответственно, а точка M делит ребро SD в отношении 1: 4, считая от вершины.
1) Укажите:
а) прямые, параллельные плоскости основания пирамиды; ответ обоснуйте;
б) прямые, скрещивающиеся с прямой DC;
в) угол наклона ребра SD к плоскости ABC;
г) линейный угол двугранного угла SDCB.
2) Постройте:
а) точку пересечения прямой LK с плоскостью ABC;
б) из точки L перпендикуляр к плоскости основания;
в) угол наклона ребра SC к плоскости основания пирамиды;
|
|
|
г) точку пересечения прямой с плоскостью ABC, проходящей через точку M параллельно прямой SA.
Обоснуйте построения.
3) Докажите, что прямая ML параллельна плоскости ABC.
|
Критерии оценивания | ||
|
Процент Результативности (правильных ответов) |
Качественная оценка индивидуальных образовательных достижений | |
| Балл (отметка) | Вербальный аналог | |
| 100-85 | отлично | |
| 84-70 | хорошо | |
| 69-50 | удовлетворительно | |
| Менее 49 | не удовлетворительно | |
|
|
|
