 |
Вариант 3. Критерии оценивания. Процент. Результативности. (правильных ответов). Качественная оценка индивидуальных образовательных достижений
|
|
|
|
Вариант 3.
1. Высота правильной треугольной пирамиды равна 4м. Боковая ее грань наклонена к плоскости основания под углом 450. Вычислить площадь боковой поверхности пирамиды.
2. Диагональ правильной четырехугольной призмы равна 7м, а диагональ боковой грани 5м. Найти боковую поверхность призмы.
3. Определить боковую поверхность правильной треугольной пирамиды, если сторона основания равна 5, а боковое ребро составляет с плоскостью основания угол 300.
Вариант 4.
1. Высота правильной четырехугольной пирамиды равна 4м. Боковая ее грань наклонена к плоскости основания под углом 300. Вычислить площадь боковой поверхности пирамиды.
2. Диагональ правильной четырехугольной призмы равна 6м и составляетс плоскостью основания 45 о. Найти боковую поверхность призмы.
3. Определить боковую поверхность правильной треугольной пирамиды, если сторона основания равна 4, а боковое ребро составляет с плоскостью основания угол 450.
|
Критерии оценивания | ||
|
Процент Результативности (правильных ответов) |
Качественная оценка индивидуальных образовательных достижений | |
| Балл (отметка) | Вербальный аналог | |
| 100-85 | отлично | |
| 84-70 | хорошо | |
| 69-50 | удовлетворительно | |
| Менее 49 | не удовлетворительно | |
Практическая работа №16 «Вероятность и её свойства»
Задание:
Задача 1. Случайная величина подчинена закону равномерного распределения на интервале (2; 5). Найти функцию распределения случайной величины Х и функцию плотности распределения вероятностей случайной величины Х. Постройте графики функции распределения и график плотности распределения случайной величины Х.
|
|
|
Задача 2. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X, равномерно распределенной на интервале (3; 7).
Задача 3. Цена деления шкалы измерительного прибора равна 0, 4. Показания прибора округляют до ближайшего деления. Найти вероятность того, что ошибка отсчета: а) превысит значение 0, 08; б) меньше 0, 08.
Задача 4. Ребро куба х измерено приближенно, причем  .
.
Рассматривая ребро куба как случайную величину, распределенную равномерно в интервале (a, b), найти математическое ожидание и дисперсию площади поверхности куба.
Задача 5. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 10 минут. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус а) менее 4 минут; б) не менее 4 минут; в) математическое ожидание случайной величины Х – времени ожидания автобуса.
Задача 6. Вычислить вероятность того, что при шести испытаниях менее четырех раз случайная величина Х – попадет в интервал (0; 2, 5), если случайная величина Х распределена по равномерному закону на отрезке [0; 4].
|
Критерии оценивания | ||
|
Процент Результативности (правильных ответов) |
Качественная оценка индивидуальных образовательных достижений | |
| Балл (отметка) | Вербальный аналог | |
| 100-85 | отлично | |
| 84-70 | хорошо | |
| 69-50 | удовлетворительно | |
| Менее 49 | не удовлетворительно | |
2. 3 Задания для проведения итогового контроля в форме экзамена
На выполнение работы отводится 180 минут. Советуем выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у вас останется время, вы можете вернуться к пропущенным заданиям. Критерии оценки:
Отметка «5» ставится, если:
|
|
|
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что учащийся не владеет
обязательными умениями по данной теме в полной мере.
Критерии ошибок:
1. К г р у б ы м ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять; незнание приемов решения задач, рассматриваемых в учебниках, а также вычислительные ошибки, если они не являются опиской;
2. К н е г р у б ы м ошибкам относятся: потеря корня или сохранение в ответе постороннего корня; отбрасывание без объяснений одного из них и равнозначные им;
3. К н е д о ч е т а м относятся: нерациональное решение, описки, недостаточность или отсутствие пояснений, обоснований в решениях.
Вариант 1.
1. Вычислить:
a)  ;
;
б) 
2. Решите уравнения:
а)  в)
в) 
б)  г)
г) 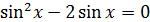
3. Решите неравенства:
а) 
б) 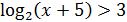
4. Найдите наибольшее и наименьшее значения функции
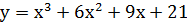 на отрезке
на отрезке 
5. Вычислите площадь фигуры, ограниченной линиями

6. Апофема правильной четырёхугольной пирамиды 6 см, высота пирамиды равна 3  см. Найдите площадь боковой и полной поверхности пирамиды.
см. Найдите площадь боковой и полной поверхности пирамиды.
Вариант 2.
1. Вычислить:
 ;
;
б) 
2. Решите уравнения:
а)  в)
в) 
|
|
|
б) 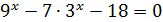 г)
г) 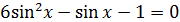
3. Решите неравенства:
а) 
б) 
4. Найдите наибольшее и наименьшее значения функции  на
на
отрезке 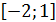
5. Вычислите площадь фигуры, ограниченной линиями 
6. Боковое ребро правильной треугольной призмы равно 9 см, а диагональ боковой грани равна 15 см. Найдите площадь боковой и полной поверхности призмы.
Вариант 3.
1. Вычислить:
а) 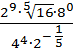
б) 
2. Решите уравнения:
а) 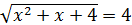 в)
в) 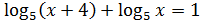
б)  г)
г) 
3. Решите неравенства:
а) 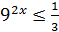
б) 
4. Найдите наибольшее и наименьшее значения функции  на
на
отрезке 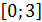
5. Вычислите площадь фигуры, ограниченной линиями

6. В правильной четырёхугольной призме сторона основания равна 12 дм, а высота 8 дм. Вычислите площади боковой и полной поверхности призмы.
Вариант 4.
1. Вычислить:
а) 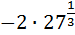
б) 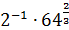
2. Решите уравнения:
а) 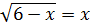 в)
в) 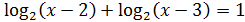
б)  г)
г) 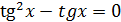
3. Решите неравенства:
а) 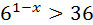
б) 
4. Найдите наибольшее и наименьшее значения функции
 на отрезке
на отрезке 
5. Вычислите площадь фигуры, ограниченной линиями
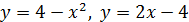
6. В правильной треугольной призме сторона основания равна 10 см., а высота 15 см. Вычислите площади боковой и полной поверхности призмы.
|
|
|


