 |
II вариант. Критерии оценивания. Процент. Результативности. (правильных ответов). Качественная оценка индивидуальных образовательных достижений
|
|
|
|
II вариант
е) наибольшее и наименьшее значения функции;
ж) область значений функции.
2. Даны графики функций y = sin x, y = cos x, y = cos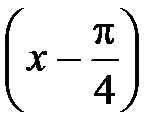 
, y = cos 
, обозначенные цифрами 1, 2, 3, 4.
а) Укажите для каждой функции номер ее графика.
б) Определите, какие из них являются четными, какие нечетными.
в) Определите, график какой из них проходит через точку 
.
|
Критерии оценивания | ||
|
Процент Результативности (правильных ответов) |
Качественная оценка индивидуальных образовательных достижений | |
| Балл (отметка) | Вербальный аналог | |
| 100-85 | отлично | |
| 84-70 | хорошо | |
| 69-50 | удовлетворительно | |
| Менее 49 | не удовлетворительно | |
Практическая работа №14 «Нахождение объема простых тел»
Задание:
I вариант
1. Объем прямоугольного параллелепипеда равен 48 см3. Вычислите объем прямоугольного параллелепипеда, у которого стороны основания в 1, 5 раза больше, а высота в 2 раза меньше.
2. Цилиндр и конус имеют равные площади боковой поверхности. Найдите, чему равна образующая конуса, если высота цилиндра 12 см, радиус основания цилиндра 9 см, а конуса 6 см.
3. Вычислите объем и площадь поверхности шара, если площадь сечения, проходящего через центр шара, равна 64p см2. Ответ укажите с точностью до целых.
II вариант
1. Объем куба равен 63 см3. Вычислите объем прямоугольного параллелепипеда, у которого стороны основания в 3 раза меньше, а высота в 4 раза больше ребра куба.
2. Цилиндр и конус имеют равные площади боковой поверхности. Найдите радиус основания цилиндра, если его высота 12 см, образующая конуса 26 см, а радиус основания конуса 10 см.
3. Объем шара равен 36p см3. Вычислите поверхность шара и площадь сечения шара плоскостью, проходящей через центр.
|
|
|
|
Критерии оценивания | ||
|
Процент Результативности (правильных ответов) |
Качественная оценка индивидуальных образовательных достижений | |
| Балл (отметка) | Вербальный аналог | |
| 100-85 | отлично | |
| 84-70 | хорошо | |
| 69-50 | удовлетворительно | |
| Менее 49 | не удовлетворительно | |
Практическая работа №15 «Площадь поверхности различных тел»
Задание:
Вариант 1
1. В основании прямого параллелепипеда лежит ромб ABCD со стороной, равной а, и углом BAD, равным 600. Плоскость ВС1D составляет с плоскостью основания угол 600. Площадь большого диагонального сечения равна 63 см2. Найти площадь полной поверхности параллелепипеда.
2. В основании пирамиды DABC лежит прямоугольный треугольник АВС, угол С = 900, угол А = 300, ВС = 10. Боковые ребра пирамиды равнонаклонены к плоскости основания. Высота пирамиды равна 5. Найти площадь боковой поверхности пирамиды.
3. Основанием пирамиды SABC служит правильный треугольник АВС, боковое ребро SA перпендикулярно основанию, а грань SBC cоставляет с ней угол в 450. Найти полную поверхность пирамиды.
Вариант 2.
1. В основании прямого параллелепипеда лежит параллелограмм ABCD со сторонами 3см и 5см. Острый угол параллелограмма равен 600. Площадь большого диагонального сечения равна 63 см2. Найти площадь полной поверхности параллелепипеда.
2. В основании пирамиды МABCD лежит ромб АВСD, АС = 8, ВD = 6. Высота пирамиды МО равна 1, где точка О - точка пересечения диагоналей. Найти площадь боковой поверхности пирамиды.
3. Основанием пирамиды SABCD служит прямоугольник АВСD, стороны которого АВ = 8см, ВС = 15см. Боковое ребро SВ перпендикулярно основанию, а ребро SD составляет с плоскостью основания угол в 600. Найти полную поверхность пирамиды.
|
|
|
