 |
Практическая работа №7. «Правила комбинаторики»
|
|
|
|
Практическая работа №7. «Правила комбинаторики»
Задание:
Решите задачи:
1. При окончании деловой встречи специалисты обменялись визитными карточками. Сколько всего визитных карточек перешло из рук в руки, если во встрече участвовали 6 специалистов?
2. В хоровом кружке занимаются 9 человек. Необходимо выбрать двух солистов. Сколькими способами это можно сделать?
3. Сколько существует вариантов рассаживания вокруг стола 6 гостей на 6 стульях?
4. Пятеро друзей сыграли между собой по одной партии в шахматы. Сколько всего партий было сыграно?
5. В меню столовой предложено на выбор 2 первых блюда, 6 вторых и 4 третьих блюда. Сколько различных вариантов обеда, состоящего из первого, второго и третьего блюда, можно составить?
6. В магазине продаются блокноты 7 разных видов и ручки 4 разных видов. Сколькими разными способами можно выбрать покупку из одного блокнота и одной ручки?
7. На прививку в медпункт отправились 7 друзей. Сколькими разными способами они могут встать в очередь у медицинского кабинета?
8. Сколько различных трёхзначных чисел можно составить при помощи цифр 4, 7, 9? (Цифры в записи числа не повторяются).
9. Сколько различных трёхзначных чисел можно составить с помощью цифр 7 и 3?
10. Сколько нечетных трёхзначных чисел можно составить из цифр 3, 4, 8, 6? (Цифры в записи числа не могут повторяться).
|
Критерии оценивания | ||
|
Процент Результативности (правильных ответов) |
Качественная оценка индивидуальных образовательных достижений | |
| Балл (отметка) | Вербальный аналог | |
| 100-85 | отлично | |
| 84-70 | хорошо | |
| 69-50 | удовлетворительно | |
| Менее 49 | не удовлетворительно | |
Практическая работа №8 «Скалярное произведение»
|
|
|
Задание:
1 Найти линейную комбинацию векторов AB - 3BC + 4CD
2 Найти длины векторов AB; BC; CD
3 Найти косинусы углов между векторами AB и BC;
4 Найти Найти (AB +CD)× AD
5 Найти ПрAB (BD + AC )
6 Выяснить, коллинеарны ли векторы AB и CD
7 Выяснить, ортогональны ли векторы AB и CD
Если:
1 A (2; 3; -1); B (0; 1; 2); C (4; -1; -1); D (2; -3; 1)
2 A (3; -1; 1); B (1; 3; 2); C (1; -1; -1); D (4; 0; 3)
|
Критерии оценивания | ||
|
Процент Результативности (правильных ответов) |
Качественная оценка индивидуальных образовательных достижений | |
| Балл (отметка) | Вербальный аналог | |
| 100-85 | отлично | |
| 84-70 | хорошо | |
| 69-50 | удовлетворительно | |
| Менее 49 | не удовлетворительно | |
Контрольная работа № 4
I вариант
1. В треугольнике ABC отрезок BO является медианой.
а) Постройте вектор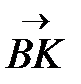 
, равный сумме векторов 
и 
.
б) Докажите, что четырехугольник BAKC является параллелограммом.
в) Выразите вектор 
через векторы 
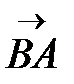и .
г) Укажите вектор, выходящий из точки B, который является разностью векторов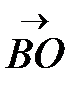 
и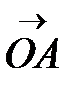 
.
2. Даны три точки с координатами: F(8; 1; 0), E(0; 0; 4), K(0; 5; 1).
а) Постройте их в декартовой системе координат.
б) Укажите, в каких координатных плоскостях или на каких координатных осях они находятся.
в) Докажите, что треугольник FKE равнобедренный.
г) Вычислите площадь треугольника FKE с точностью до целых.
II вариант
1. Диагонали прямоугольника ABCD пересекаются в точке O.
а) Постройте вектор 
, равный сумме векторов 
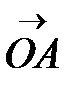и 
.
б) Докажите, что четырехугольник OAFD – ромб.
в) Выразите вектор 
через векторы 
и 
.
г) Укажите вектор, выходящий из точки B, который является разностью векторов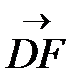 
и 
.
2. Даны три точки с координатами: P(4; 0; 0), K(0; 2; 0), T(2; 0; 4).
а) Постройте их в прямоугольной системе координат.
б) Укажите, на каких координатных осях или в каких координатных плоскостях они находятся.
|
|
|
в) Докажите, что треугольник PKT – равнобедренный.
г) Вычислите площадь треугольника PKT.
|
Критерии оценивания | ||
|
Процент Результативности (правильных ответов) |
Качественная оценка индивидуальных образовательных достижений | |
| Балл (отметка) | Вербальный аналог | |
| 100-85 | отлично | |
| 84-70 | хорошо | |
| 69-50 | удовлетворительно | |
| Менее 49 | не удовлетворительно | |
|
|
|
