 |
Примеры оценивания решений заданий 13
|
|
|
|
ФЕДЕРАЛЬНАЯ СЛУЖБА ПО НАДЗОРУ В СФЕРЕ ОБРАЗОВАНИЯ И НАУКИ
_______________________________________________________________________
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ НАУЧНОЕ УЧРЕЖДЕНИЕ
«ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ»
Методические материалы для председателей и членов предметных комиссий субъектов Российской Федерации
По проверке выполнения заданий с развернутым ответом экзаменационных работ ЕГЭ 2017 года
МАТЕМАТИКА
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ОЦЕНИВАНИЮ ВЫПОЛНЕНИЯ
ЗАДАНИЙ С РАЗВЕРНУТЫМ ОТВЕТОМ
Москва
Руководитель федеральной комиссии по разработке контрольных измерительных материалов для проведения государственной итоговой аттестации по образовательным программам основного общего и среднего общего образования по математике И.В. Ященко, в.н.с. ФГБНУ «ФИПИ».
Авторы–составители: И.Р. Высоцкий, О.Н. Косухин, П.В. Семёнов, А.В. Семенов, А.С. Трепалин.
Методические материалы для председателей и членов предметных комиссий субъектов Российской Федерации по проверке выполнения заданий с развернутым ответом экзаменационных работ ЕГЭ 2017 г. по математике подготовлены в соответствии с Тематическим планом работ Федерального государственного бюджетного научного учреждения «Федеральный институт педагогических измерений» на 2017 г. Пособие предназначено для подготовки экспертов по оцениванию заданий с развернутым ответом, которые являются частью контрольных измерительных материалов (КИМ) для сдачи единого государственного экзамена (ЕГЭ) по математике.
В методических материалах дается краткое описание структуры контрольных измерительных материалов 2017 г. по математике, характеризуются типы заданий с развернутым ответом, используемые в КИМ ЕГЭ по математике, и критерии оценки выполнения заданий с развернутым ответом, приводятся примеры оценивания выполнения заданий и даются комментарии, объясняющие выставленную оценку.
|
|
|
В пособии использованы ответы участников ЕГЭ 2013–2015 гг.,
а также диагностических и тренировочных работ.
Авторы будут благодарны за замечания и предложения по совершенствованию пособия.
© И.Р. Высоцкий, О.Н. Косухин, П.В. Семёнов, А.В. Семенов, А.С. Трепалин, 2017
© Федеральный институт педагогических измерений. 2017
СОДЕРЖАНИЕ
ВВЕДЕНИЕ.. 4
1. Критерии проверки и оценка решений заданий 13 (15 в 2015 г., С1 ранее) вариантов КИМ ЕГЭ-2017 5
2. Критерии проверки и оценка решений заданий 14 (16 в 2015 г., С2 ранее) вариантов КИМ ЕГЭ–2017 13
3. Критерии проверки и оценка решений заданий 15 (18 в 2015 г., С3 ранее) вариантов КИМ ЕГЭ–2017 22
4. Критерии проверки и оценка решений заданий 16 (18 в 2015 г., С4 ранее) вариантов КИМ ЕГЭ–2017 32
5. Критерии проверки и оценка решений заданий 17 (19 в 2015 г.) вариантов КИМ ЕГЭ–2017 41
6. Критерии проверки и оценка решений заданий 18 (20 в 2015 г., С5 ранее) вариантов КИМ ЕГЭ–2017 51
7. Критерии проверки и оценка решений заданий 19 (21 в 2015 г., С6 ранее) вариантов КИМ ЕГЭ-2017 63
ВВЕДЕНИЕ
Общие позиции и характер оценивания выполнения заданий в целом повторяют прошлогодние. Небольшие видоизменения и корректировки формулировок в содержании критериев оценивания для конкретного задания могут иметь место в тех случаях, когда необходимость подобного рода уточнений диктуется содержанием и структурой самого задания.
Более подробное описание заданий с развернутым ответом и критериев оценивания их выполнения представлены ниже, в начале каждого из параграфов 1–7.
Так как нумерация заданий с развернутым ответом трижды менялась за четыре последних года, то в тексте настоящих методических материалов мы довольно часто приводим не только нумерацию 2017 года, но и две предыдущие. Например, оборот «задание 18 (=20 =С5)» означает, что мы имеем дело с заданием 18 этого года, которое соответствует 20-й позиции в ЕГЭ 2015 г. и, соответственно, заданиям С5 2010–2014 гг.
|
|
|
Извлечения из Методических рекомендаций Рособрнадзора по формированию и организации работы предметных комиссий субъекта Российской Федерации при проведении государственной итоговой аттестации по образовательным программам среднего общего образования
Во время работы экспертам запрещается:
· самостоятельно изменять рабочие места;
· копировать и выносить из помещений, где осуществляется проверка, экзаменационные работы, критерии оценивания, протоколы проверки экзаменационных работ, а также разглашать посторонним лицам информацию, содержащуюся в указанных материалах;
· иметь при себе и (или) пользоваться средствами связи, фото и видеоаппаратурой, портативными персональными компьютерами (ноутбуками, КПК и другими), кроме специально оборудованного в помещениях ПК рабочего места с выходом в информационно-телекоммуникационную сеть «Интернет» для обеспечения возможности уточнения экспертами изложенных в экзаменационных работах участников ГИА фактов (например, сверка с источниками, проверка приведенных участниками ГИА фамилий, названий, фактов и т.п.);
· без уважительной причины покидать аудиторию;
· переговариваться, если речь не идет о консультации у председателя ПК или у эксперта, назначенного по решению председателя ПК консультантом;
если у эксперта возникают вопросы или проблемы, он должен обратиться к председателю ПК или лицу, назначенному председателем ПК консультантом
1. Критерии проверки и оценка решений заданий 13 (15 в 2015 г., С1 ранее) вариантов КИМ ЕГЭ-2017
Задания №13 занимают одну из важнейших позиций в структуре КИМ. К их выполнению в 2015 г. приступало более 60% участников профильного единого государственного экзамена (ЕГЭ), а положительные баллы получили более 30% всех участников. Успешность выполнения заданий этого типа является характеристическим свойством, различающим базовый и профильный уровни подготовки учащихся. Поэтому при подготовке выпускников к экзамену решению заданий подобного уровня следует уделять много внимания.
|
|
|
Подчеркнем, что выделение решения уравнения в отдельный пункт а прямо указывает участникам экзамена на необходимость полного решения предложенного уравнения: при отсутствии в тексте конкретной работы ответа на вопрос п. а задание №13 следует оценивать не более чем 1 баллом.
В дискуссиях с представителями региональных групп экспертов неоднократно высказывалось предложение о смягчении критериев выставления 1 балла. А именно, предлагалось поступать так и в тех случаях, когда в решении п. а допущена вычислительная ошибка или описка, не повлиявшая на полноту всего решения. В критериях оценивания заданий с развернутым ответом ЕГЭ 2014–2017 эти предложения были учтены.
| Содержание критерия, №15 УММ–2015 | Баллы |
| Обоснованно получены верные ответы в обоих пунктах | |
| Обоснованно получен верный ответ в пункте а или в пункте б ИЛИ получен ответ неверный из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов – пункта а и пункта б | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
| Содержание критерия, №15 ЕГЭ–2015 | Баллы |
| Обоснованно получены верные ответы в обоих пунктах | |
| Обоснованно получен верный ответ в пункте а или в пункте б ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов — пункта а и пункта б | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Небольшое уточнение с «неверный ответ» до «неверные ответы» подчеркивает тот факт, что 1 балл допускается ставить в тех случаях, когда единственная вычислительная ошибка (описка) стала причиной того, что неверны оба ответа, полученные при выполнении п. а и п. б.
Сохранена такая структура критериев и в 2017 г.
В демонстрационном варианте ЕГЭ это задание остаётся практически неизменным.
|
|
|
Задача 13 (демонстрационный вариант 2017 г).
а) Решите уравнение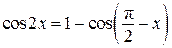 
.
б) Найдите все корни этого уравнения, принадлежащие промежутку 
.
Решение. а) Преобразуем уравнение:
; 
; 
,
откуда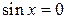 
или 
.
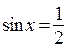Из уравнения 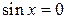находим: 
, где 
.
Из уравнения 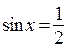находим: 
, где .
б) С помощью числовой окружности отберём корни уравнения, принадлежащие промежутку .
Получаем числа: 
; 
; 
.
Ответ: а) 
, 
, .
б) ; ; .
Комментарий. Отбор корней может быть обоснован и любым другим способом: с помощью графика, решения двойных неравенств и т.п.
Возвращаясь к критериям, если:
(1) уравнение (см. пример выше) верно сведено к простейшим тригонометрическим уравнениям 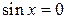и 
;
(2) эти простейшие уравнения не решены или решены с ошибкой;
(3) но при этом отбор корней исходного уравнения верно произведён с помощью тригонометрической окружности, а не по неверно найденным корням простейших тригонометрических уравнений, то по критериям можно выставить 1 балл (получен верный ответ в п. б, а его получение обосновано верным сведением к простейшим уравнениям).
В то же время, при наличии (1) и (2) и «верного» отбора по неверно решенным простейшим уравнениям следует выставлять 0 баллов: любые ошибки, допущенные в тригонометрических формулах, в нахождении значений тригонометрических функций не относятся к вычислительным.
Примеры оценивания решений заданий 13
Пример 1.
а) Решите уравнение 
.
б) Найдите все корни этого уравнения, принадлежащие промежутку 
.
Ответ: а) 
; б) 
.
Комментарий.
Работа не пустая. Она цитирует УММ 2014 года, где за эту работу был выставлен 1 балл. Объяснение состояло в том, что при переходе от 
к 
допущена очевидная вычислительная ошибка, а уравнение решено верно, и затем произведён отбор. К сожалению, в этом отборе есть и описка в 3), есть и ошибка в 1): отобранный корень не принадлежит нужному отрезку.
Оценка эксперта: 0 баллов.
Пример 2.
а) Решите уравнение 
.
б) Укажите корни этого уравнения, принадлежащие отрезку 
.
Ответ: а)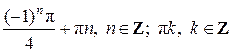 
; б) 
.
Комментарий.
Типичный пример выставления 1 балла по критериям 2014, 2015 гг. При решении второго простейшего тригонометрического уравнения «пропал» множитель 2 в периоде. Но верный отбор корней произведён не по формуле, а по тригонометрической окружности.
Оценка эксперта: 1 балл.
Пример 3.
а) Решите уравнение 
.
б) Найдите все корни этого уравнения, принадлежащие отрезку 
.
Ответ: а) 
, 
; б)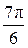 
; 
; 
.
Комментарий.
Правильные ответы обоснованно получены в пунктах а и б.
Оценка эксперта: 2 балла.
Пример 4.
а) Решите уравнение 
.
б) Найдите все корни этого уравнения, принадлежащие промежутку 
.
|
|
|
Ответ: а) 
; б) 
.
Комментарий. Нигде в решении нет описания значений параметра k, но при отборе корней явно указано целое значение. Считаем, что выставление наивысшего балла возможно.
Оценка эксперта: 2 балла.
Пример 5.
а) Решите уравнение 
.
б) Найдите все корни этого уравнения, принадлежащие промежутку 
.
Ответ: а) 
; б)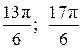 
.
Комментарий. Странный случай. В тексте много верных вещей. В п. а сначала написан верный ответ 
. Но потом появляется угол в 
(!!!?). В результате оба ответа неверны не из-за вычислительной ошибки.
Оценка эксперта: 0 баллов.
Пример 6.
а) Решите уравнение 
.
б) Найдите все корни этого уравнения, принадлежащие промежутку 
.
Ответ: а) 
; б) 
.
Комментарий.
Практически всё верно, только отобранные корни не принадлежат нужному отрезку. Верно выполнен только первый пункт.
Оценка эксперта: 1 балл.
2. Критерии проверки и оценка решений заданий 14 (16 в 2015 г., С2 ранее) вариантов КИМ ЕГЭ–2017
Задания 14 являются практически полным аналогом заданий №16 и С2 КИМ ЕГЭ предыдущих лет. Стереометрическая задача позиционируется как задача для большинства успевающих учеников, а не только для избранных. В связи с этим в КИМах предлагается достаточно простая задача по стереометрии, решить которую возможно с минимальным количеством геометрических построений и технических вычислений. Итак, в заданиях 14 прежними остались уровень сложности, тематическая принадлежность (геометрия многогранников) и максимальный балл (2 балла) за их выполнение.
Несколько изменилась структура постановки вопроса. Как и в прошлом году, она разделена на пункты а и б примерно так же, как и задание 13. Соответственно уточнился и общий характер оценивания выполнения решений. Для получения 2 баллов нужно, чтобы выполнялись два условия одновременно (конъюнкция), а для получения 1 балла хватает выполнения хотя бы одного из этих условий (дизъюнкция).
| Содержание критерия, задание №14 (=16), 2015 и 2016 г. | Баллы |
| Имеется верное доказательство утверждения пункта а И обоснованно получен верный ответ в пункте б | |
| Имеется верное доказательство утверждения пункта а ИЛИ обоснованно получен верный ответ в пункте б | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Пункт а в заданиях 14 может по разному соотноситься с пунктом б. А именно, он может быть утверждением независимым от б, дополняющим или проверяющим понимание общей конструкции. Возможен и второй вариант, когда в пункте а следует доказать утверждение, необходимое для полной корректности вычислений в пункте б. В первой ситуации независимость условий а и б приводит и к независимости проверки их выполнения. Во второй ситуации вполне может встретиться примерно следующий текст.
«Задание 16……. а) Докажите, что…; б) Найдите площадь….
Решение.
У меня а) не получилось. Используем а) при решении б)… далее верное и обоснованное (без выполнения пункта а) вычисление……».
Хуже того, вместо честного признания о «нерешаемости» а может быть предъявлено неполное и, даже, неверное доказательство. И в том, и в другом случае за верное решение пункта б следует выставлять 1 балл. Позиция разработчиков КИМ состоит в том, что в первую очередь следует поощрять за достижения, а не наказывать за промахи. Тем самым, часть «обоснованно получен верный ответ в пункте б» критерия на 1 балл более точно было бы сформулировать как «обоснованно (по модулю п. а) получен верный ответ в пункте б».
Отметим также часто задаваемый экспертами вопрос, связанный с проверкой решения задач на нахождение угла. Вид ответа может отличаться от приведённого в критериях по проверке заданий с развёрнутым ответом. Это отличие не может служить основанием для снижения оценки. (Кстати, последнее верно для проверки любого задания, не обязательно задания по стереометрии). Главное, чтобы ответ был правильным. Например, если в образце решения стоит 
, а у выпускника в ответе 
, то справедливость равенства = эксперту следует проверить самостоятельно.
Отдельно скажем о применении различных формул аналитической геометрии, которыми несколько излишне увлекаются некоторые специалисты. Разумеется, никакого запрета на их использование нет. Однако, если по критериям 2014 года адекватное использование некоторой формулы с допущенной вычислительной ошибкой можно оценить в 1 балл, то условие «обоснованно получен верный ответ в пункте б» критериев 2017 года в таком случае уже не выполнено и (если нет доказательства а) следует выставлять 0 баллов.
Задание 1 (№16, ЕГЭ 2015 г).
В основании четырёхугольной пирамиды 
лежит прямоугольник 
со сторонами 
и 
. Длины боковых рёбер пирамиды 
, 
, 
.
а) Докажите, что 
— высота пирамиды.
б) Найдите угол между прямыми 
и 
.
Решение.
|
а) В треугольнике 
имеем:
,
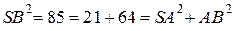поэтому треугольник прямоугольный с гипотенузой 
и прямым углом . Аналогично, из равенства
получаем, что 
. Так как прямая перпендикулярна прямым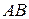 
и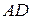 
, прямая перпендикулярна плоскости 
.
б) На прямой 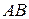отметим такую точку 
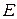, что 
— параллелограмм, тогда 
и 
. Найдём угол 
. По теореме Пифагора:
; 
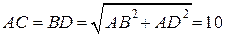и 
.
По теореме косинусов:
; 
; 
.
Искомый угол равен 
. Ответ: б) .
Задание 2 (№16, ЕГЭ 2015 г).
В правильной треугольной пирамиде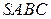 
сторона основания 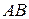равна 60, а боковое ребро 
равно 37. Точки 
и 
— середины рёбер и 
соответственно. Плоскость 
содержит прямую 
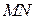и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость делит медиану 
основания в отношении 
, считая от точки 
.
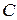б) Найдите расстояние от вершины 
до плоскости .
|
Решение.
а) Прямая 
параллельна плоскости 
, поэтому сечение пересекает плоскость по прямой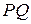 
, параллельной . Рассмотрим плоскость 
. Пусть 
— точка пересечения этой плоскости и прямой , 
— точка пересечения этой плоскости
и прямой ,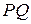 
— центр основания пирамиды. Плоскости и 
перпендикулярны плоскости , поэтому прямая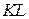 
перпендикулярна плоскости , а значит, параллельна прямой 
. Поскольку — средняя линия треугольника 
, точка является серединой 
. Следовательно, — середина 
. Медиана 
треугольника делится точкой в отношении 
. Значит, 
.
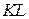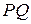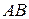б) Прямая перпендикулярна и , поэтому прямая перпендикулярна плоскости . Прямые и 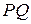параллельны, значит, расстояние от вершины до плоскости сечения равно расстоянию
от точки 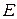до плоскости сечения, то есть 
.
Ответ: б) 
.
|
|
|
