 |
Примеры оценивания решений заданий 18
|
|
|
|
Пример 1. Система, см. текст, имеет ровно два решения. Ответ:  .
.
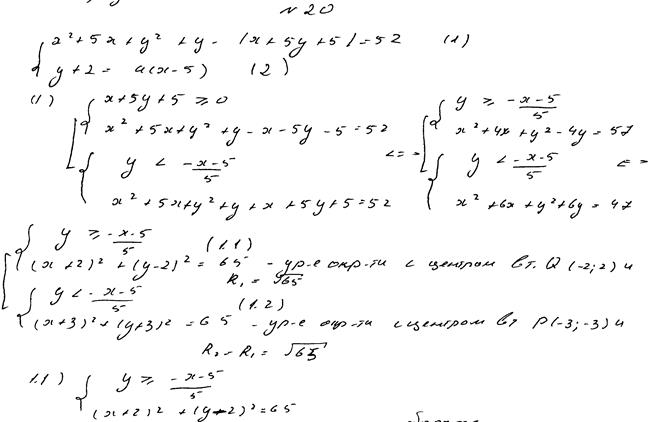






Комментарий. Ход решения ясен, изложен более чем подробно. Ошибок нет, кроме прокола с невключением в ответ концов промежутка.
Довольно показательный пример, когда переход от геометрического способа к алгебраическому способу решения запутывает ситуацию.
Оценка эксперта: 3 балла.
Пример 2. Условие см. текст выше, Задача 1. Ответ:  ,
,  .
.

Комментарий. Деликатный случай. С одной стороны, есть явное и полное понимание ситуации. С другой стороны, в самом начале допущена ошибка с включением прямой  во множество решений. И только из-за этого в дальнейшем был произведен отбор, давший неверный ответ. Более 1 балла поставить нельзя. На 1 балл условие критерия «Задача верно сведена…» не выполнено, и условие «получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения» не выполнено. Всё-таки, ставить 0 баллов.
во множество решений. И только из-за этого в дальнейшем был произведен отбор, давший неверный ответ. Более 1 балла поставить нельзя. На 1 балл условие критерия «Задача верно сведена…» не выполнено, и условие «получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения» не выполнено. Всё-таки, ставить 0 баллов.
Оценка эксперта: 0 баллов.
Пример 3. Система, см. текст, имеет ровно два решения. Ответ:  .
.

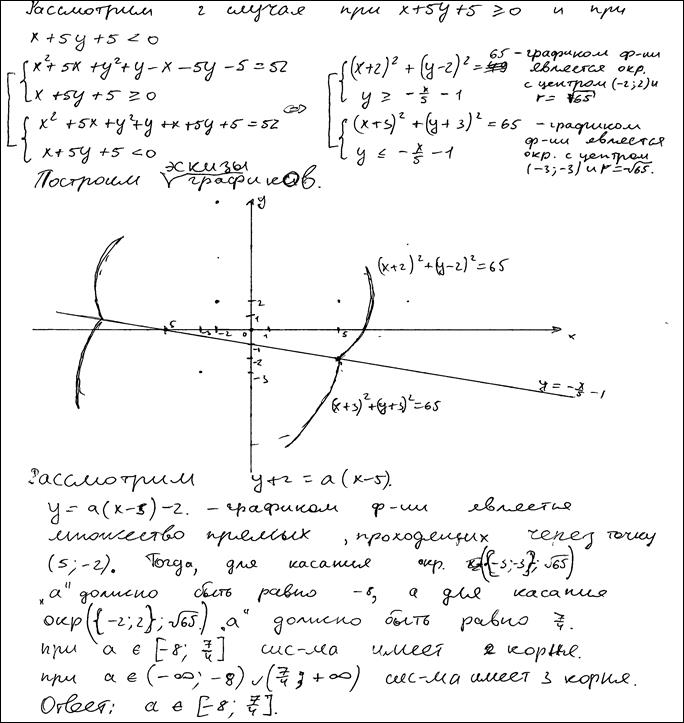
Комментарий. Ответ верен, но только нет даже намека на обоснование того, почему для касания  «должно быть равно -8» или «…7/4».
«должно быть равно -8» или «…7/4».
Оценка эксперта: 4 балла.
Пример 4. Найдите все значения  , при каждом из которых система
, при каждом из которых система  имеет ровно два различных решения.
имеет ровно два различных решения.
Ответ:  ,
,  .
.

Комментарий.
Довольно редкий случай, когда в точности по критериям можно поставить 2 балла. О трёх баллах речь в принципе не идет, так как автор практически полностью забыл учесть условие 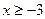 и поэтому отбросил случай
и поэтому отбросил случай  .
.
Оценка эксперта: 2 балла.
Пример 5. Найдите все значения  , при каждом из которых система уравнений
, при каждом из которых система уравнений

имеет ровно два решения.
Ответ: 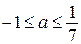 .
.
|
|
|

Комментарий.
Никакого ответа нет, но работа «не пустая»: верно приведены уравнения окружностей в каждом случае раскрытия модуля (правда, без особых обоснований).
Тем не менее, невозможно считать, что, см. критерии, «Задача верно сведена к исследованию взаимного расположения дуг окружностей и прямых (аналитически или графически)». Для этого, как минимум, не хватает пучка прямых, проходящих через точку (2;-1).
Оценка эксперта: 0 баллов.
Пример 6.
Найдите все значения  , при каждом из которых система уравнений
, при каждом из которых система уравнений
 имеет ровно два решения.
имеет ровно два решения.
Ответ: 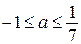 .
.

Комментарий. По сравнению с предыдущим примером – чистый 1 балл. Оба уравнения системы верно проинтерпретированы геометрически. Правда, вновь очень лаконично. Более ничего практически нет.
Оценка эксперта: 1 балл.
7. Критерии проверки и оценка решений заданий 19 (21 в 2015 г., С6 ранее) вариантов КИМ ЕГЭ-2017
Содержательно задание №19 (бывшее 21 и С6) проверяет в первую очередь не уровень математической (школьной) образованности, а уровень математической культуры. Вопрос формирования соответствующей культуры – вещь деликатная и, в целом, формируемая на протяжении нескольких лет.
В то же время, изменения в формате ЕГЭ связаны, в частности, с тем, что это задание по своему тематическому содержанию стало элементарнее, а для его решения, формально, достаточно простейших сведений. По этой причине, например, в ЕГЭ–2015 даже в весьма средней группе с первичным баллом от 11 до 14 положительные баллы за выполнение задания №21 получили 7,2% участников, т.е. оно перестало отпугивать выпускников.
В связи этим хотелось бы подчеркнуть, что никаких фактов из теории чисел типа теоремы Вильсона, чисел Мерсенна, малой теоремы Ферма, теории сравнений и т.п. для решения этих заданий не требуется. Тот, кто эти факты знает, разумеется, может их использовать, но, подчёркиваем, при решении всегда можно обойтись и без них.
|
|
|
Условия задания №19, как и прежних заданий С6, разбиты на пункты. По существу, задача разбита на ряд подзадач (частных случаев), последовательно решая которые можно в итоге справится с ситуацией в целом. Как правило, решение п. а весьма несложно и использует умение сконструировать некоторый конкретный пример. В соответствии с таким делением условий, критерии, начиная с 2011 года стали более формализованными. Их текст практически никак не использует тематическую или содержательную фабулу конкретной задачи. Такие изменения были предприняты для большей согласованности и унификации выставляемых экспертами оценок.
Ниже процитированы три задачи из материалов ЕГЭ 2014 и 2015 гг., их решения, ответы и критерии проверки, действовавшие на соответствующий год проведения экзамена. Интересно отметить, что в самой ранней задаче 3 еще не было деления на пункты. В задаче 1 в скобках приведены также числовые параметры версии этой же задачи из другого варианта. Далее в Части 1 приведены 6 примеров решений этих задач на ЕГЭ вместе с комментариями по оценке и самими оценками. Подчеркнём, что каждая задача оценивалась по критериям соответствующего года проведения ЕГЭ.
Задача 1.
Семь экспертов оценивают кинофильм. Каждый из них выставляет оценку — целое число баллов от 0 до 10 (от 1 до 15) включительно. Известно, что все эксперты выставили различные оценки. По старой системе оценивания рейтинг кинофильма — это среднее арифметическое всех оценок экспертов. По новой системе оценивания рейтинг кинофильма вычисляется следующим образом: отбрасываются
наименьшая и наибольшая оценки и подсчитывается среднее арифметическое пяти оставшихся оценок.
а) Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться  ? (
? (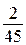 )?
)?
б) Может ли эта разность рейтингов, вычисленных по старой и новой системам оценивания, равняться  ? (
? (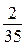 )?
)?
в) Найдите наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания.
Решение.
Обозначим рейтинг кинофильма, вычисленный по старой системе оценивания, через  , а рейтинг кинофильма, вычисленный по новой системе оценивания, через
, а рейтинг кинофильма, вычисленный по новой системе оценивания, через  .
.
а) Заметим, что  ,
,  , где
, где  и
и  — некоторые натуральные числа. Значит,
— некоторые натуральные числа. Значит,  . Если
. Если  , то
, то  , что невозможно. Таким образом, разность рейтингов, вычисленных по старой и новой системам оценивания, не может равняться
, что невозможно. Таким образом, разность рейтингов, вычисленных по старой и новой системам оценивания, не может равняться  .
.
|
|
|
б) Например, для оценок экспертов 0, 1, 2, 4, 7, 8, 9 разность рейтингов, вычисленных по старой и новой системам оценивания, равна
 .
.
в) Пусть  — наименьшая из оценок,
— наименьшая из оценок,  — наибольшая, а
— наибольшая, а  — сумма остальных пяти оценок. Тогда
— сумма остальных пяти оценок. Тогда

Для оценок экспертов 0, 1, 2, 3, 4, 5, 10 разность  равна
равна  . Значит, наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания, равно
. Значит, наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания, равно  . Ответ: а) нет (нет); б) да (да); в)
. Ответ: а) нет (нет); б) да (да); в)  .
.
| Содержание критерия, задача №1 | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получен один из следующих результатов: — обоснованное решение п. а; — пример в п. б; — искомая оценка в п. в; — пример в п. в, обеспечивающий точность предыдущей оценки | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Задача 2.
а) Приведите пример четырёхзначного числа, произведение цифр которого
в 10 раз больше суммы цифр этого числа.
б) Существует ли такое четырёхзначное число, произведение цифр которого в 175 раз больше суммы цифр этого числа?
в) Найдите все четырёхзначные числа, произведение цифр которых в 50 раз больше суммы цифр этого числа.
Решение.
а) Произведение цифр числа 2529 равно 180, а сумма цифр равна 18, то есть
в 10 раз меньше.
б) Предположим, что такое число  существует и
существует и  ,
,  ,
,  ,
,  — его цифры. Заметим, что среди этих цифр не может быть нулей, так как иначе
— его цифры. Заметим, что среди этих цифр не может быть нулей, так как иначе
их произведение было бы равно нулю. Имеем:  . Правая часть этого равенства делится на 25, поэтому среди цифр найдутся две цифры 5. Так как при перестановке местами цифр числа
. Правая часть этого равенства делится на 25, поэтому среди цифр найдутся две цифры 5. Так как при перестановке местами цифр числа  равенство
равенство  остаётся верным, то без ограничения общности можно считать, что в числе
остаётся верным, то без ограничения общности можно считать, что в числе  цифры
цифры  и
и  равны 5. Тогда
равны 5. Тогда  . Получаем противоречие.
. Получаем противоречие.
|
|
|
в) Предположим, что такое число  существует и
существует и  ,
,  ,
,  ,
,  — его цифры. Как и ранее, заметим, что среди этих цифр не может быть нулей, так как иначе их произведение было бы равно нулю. Имеем:
— его цифры. Как и ранее, заметим, что среди этих цифр не может быть нулей, так как иначе их произведение было бы равно нулю. Имеем: 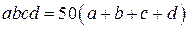 . Правая часть этого равенства делится на 25, поэтому среди цифр найдутся две цифры 5. Без ограничения общности будем считать, что
. Правая часть этого равенства делится на 25, поэтому среди цифр найдутся две цифры 5. Без ограничения общности будем считать, что  . Тогда
. Тогда  . Так как правая часть последнего равенства делится на 2, то либо
. Так как правая часть последнего равенства делится на 2, то либо  , либо
, либо  делится на 2. Будем считать, что на 2 делится
делится на 2. Будем считать, что на 2 делится  .
.
Если  , то
, то  , что невозможно.
, что невозможно.
Если  , то
, то  ;
; 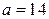 , что невозможно.
, что невозможно.
Если  , то
, то 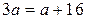 ;
;  ;
;  . Число
. Число  и все числа, получаемые из него перестановкой цифр, удовлетворяют условию задачи.
и все числа, получаемые из него перестановкой цифр, удовлетворяют условию задачи.
Если  , то
, то 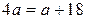 ;
; 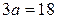 ;
;  . Этот вариант также получается
. Этот вариант также получается
из предыдущего перестановкой цифр.
Ответ: а) например, 2529; б) нет; в) Число 8655 и все числа, получаемые
из него перестановкой цифр (всего 12 чисел).
| Содержание критерия, задача №2 | Баллы |
| Верно построен пример в п. а и обоснованно получены верные ответы в п. б и п. в | |
| Обоснованно получен ответ в п. в и один из следующих результатов: — пример в п. а; — обоснованное решение п. б | |
| Верно построен пример в п. а и обоснованно получен ответ в п. б ИЛИ обоснованно получен верный ответ в п. в | |
| Верно построен пример в п. а ИЛИ обоснованно получен верный ответ в п. б | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Задача 3.
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы
в каждой группе было хотя бы одночисло. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы
из единственного числа среднее арифметическое равно этому числу).
а) Могут ли быть одинаковыми два из этих трёх значений средних арифметических в группах из разного количества чисел?
б) Могут ли быть одинаковыми все три значения средних арифметических?
в) Найдите наименьшее возможное значение наибольшего из получаемых трёх средних арифметических.
Решение.
а) Например, для групп  и
и  средние значения равны 7.
средние значения равны 7.
б) Допустим, что это возможно. Пусть все средние значения равны  .
.
В каждой группе от 1 до 8 натуральных чисел, поэтому  , где
, где  — натуральное число и
— натуральное число и  . С другой стороны, пусть группы состоят из
. С другой стороны, пусть группы состоят из  ,
,  и
и  чисел. Тогда суммы чисел в группах равны
чисел. Тогда суммы чисел в группах равны 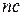 ,
,  и
и  соответственно, а общая сумма всех 10 чисел равна 61 и равна
соответственно, а общая сумма всех 10 чисел равна 61 и равна 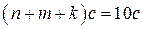 . Поэтому
. Поэтому  ;
;  . Это противоречит тому, что знаменатель числа
. Это противоречит тому, что знаменатель числа  не превосходит 8.
не превосходит 8.
в) Пусть группы состоят из  ,
,  и
и  чисел, а средние значения равны
чисел, а средние значения равны  ,
,  и
и  соответственно. Если
соответственно. Если  ,
,  ,
,  , то
, то
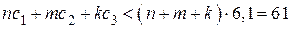 ,
,
что противоречит условию. Значит, хотя бы одно из чисел  ,
,  ,
, 
не меньше 6,1. Поэтому максимальное из этих чисел не меньше 6,1. При этом каждое из этих чисел имеет вид  , где
, где  — натуральное число
— натуральное число
и  , поэтому максимальное из этих чисел не меньше
, поэтому максимальное из этих чисел не меньше  .
.
|
|
|
Покажем, что максимальное из этих чисел не может равняться  .
.
Пусть 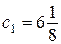 . Тогда первая группа состоит из 8 чисел, сумма которых
. Тогда первая группа состоит из 8 чисел, сумма которых
равна  . Значит, каждая из других двух групп состоит из одного числа, причём сумма двух чисел из второй и третьей групп равна 12.
. Значит, каждая из других двух групп состоит из одного числа, причём сумма двух чисел из второй и третьей групп равна 12.
Но тогда одно из этих чисел больше 6, поэтому максимальное среднее не меньше 7. Получаем, что максимальное из чисел  ,
,  ,
,  не меньше
не меньше  .
.
Покажем, что максимальное из чисел  ,
,  ,
,  может равняться
может равняться  . Это так для групп
. Это так для групп  ,
,  ,
, 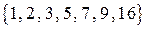 :
:  ,
,  .
.
Ответ: а) да; б) нет; в)  .
.
| Содержание критерия, задача №3 | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получен один из следующих результатов: — обоснованное решение п. а; — обоснованное решение п. б; — искомая оценка в п. в; — пример в п. в, обеспечивающий точность предыдущей оценки | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
|
|
|


