 |
Примеры оценивания решений заданий 15
|
|
|
|
Пример 1.
Решите неравенство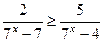 
.
Ответ: 
.
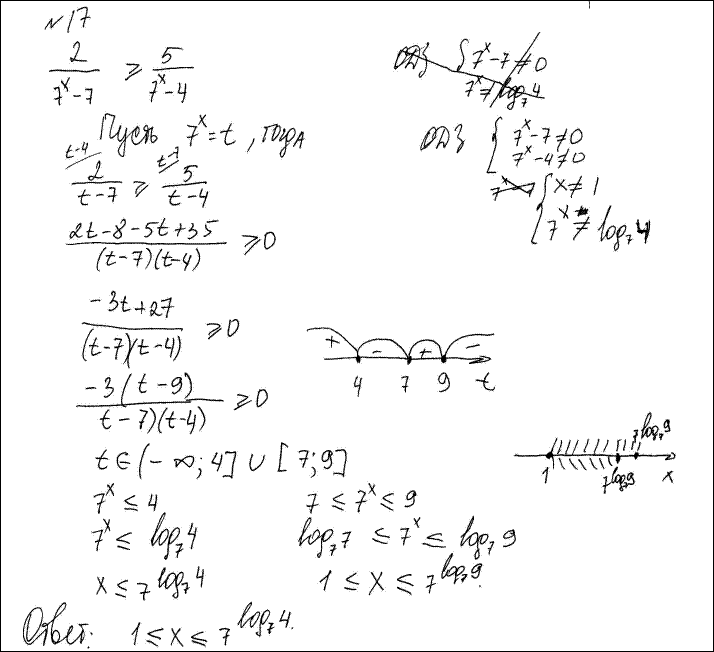
Комментарий. Хотя рациональное неравенство «почти» решено, в работе много ошибок. Похоже, автор не разобрался в логарифмах даже на простейшем уровне.
Оценка эксперта: 0 баллов.
Пример 2.
Решите неравенство 
.
Ответ: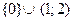 
.
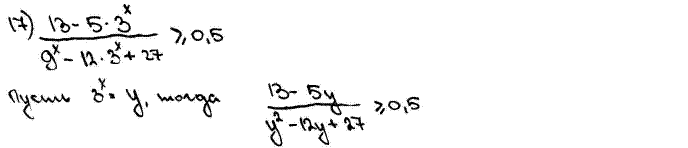
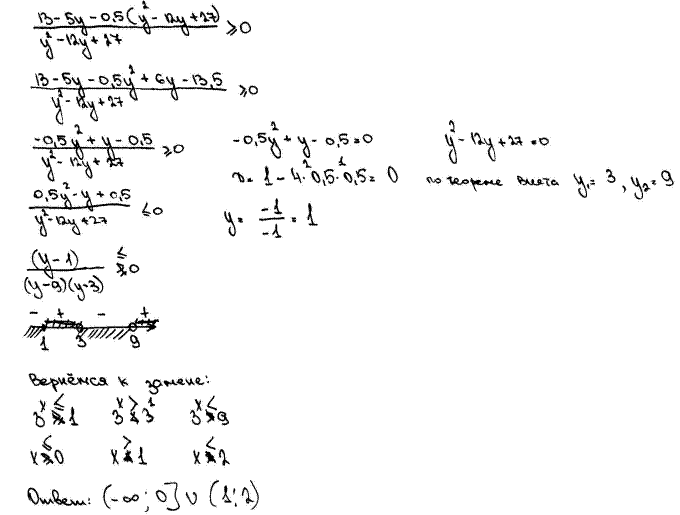
Комментарий. Можно отметить верную последовательность всех шагов решения, за исключением неравенства с множителем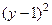 
. Далее, конечно, ошибка в применении метода интервалов. Все решения найдены, но к ним «добавлены» посторонние решения. В результате – ответ неверный.
Оценка эксперта: 0 баллов.
Пример 3.
Решите неравенство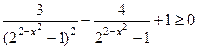 
.
Ответ: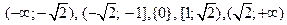 
.
.
Комментарий. В результате компенсирующих ошибок и частично верных утверждений получена «часть» множества решений неравенства. Но имеются грубейшие ошибки.
Оценка эксперта. 0 баллов.
Пример 4.
Решите неравенство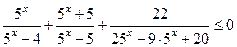 
.
Ответ: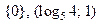 
.
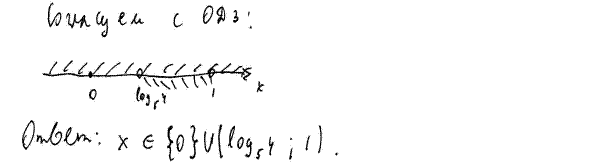
Комментарий. Можно отметить не самый удачный путь к «цели», но способ решения не оценивается. Ответ правильный и получен с приемлемым обоснованием.
Оценка эксперта. 2 балла.
Пример 5.
Решите неравенство 
.
Ответ: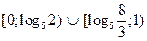 
.
Комментарий.
Вычислительных ошибок в ходе преобразований нет. Есть грубая ошибка в преобразовании первого же неравенства, которое решается по правилу пропорции (см. пунктиры).
Судя по тексту решения, его автор неверно усвоил совет типа «если всё положительно, то от знаменателей можно избавляться крест-накрест»: ведь не просто так написано, что 3/2 > 0.
Оценка эксперта: 0 баллов.
Пример 6.
Решите неравенство 
.
Ответ: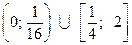 
.
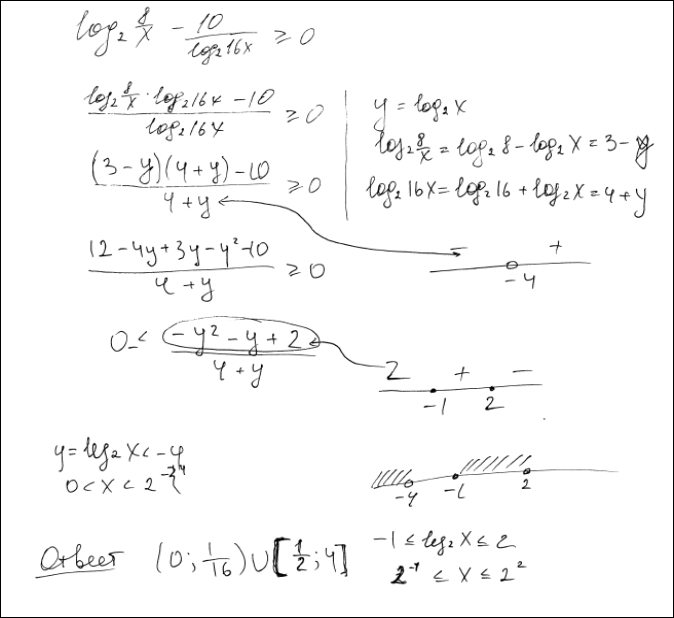
Комментарий. Типичный 1 балл. Путаница в корнях квадратного уравнения, а потом всё верно.
|
|
|
Оценка эксперта: 1 балл.
Пример 7 Условие см. пример 1. Ответ: .
Комментарий. Ответ неверный, все шаги решения присутствуют, но «случайно» использовалось верное неравенство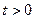 
при записи значений x. Это не может трактоваться как "получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения".
Оценка эксперта: 0 баллов.
4. Критерии проверки и оценка решений заданий 16 (18 в 2015 г., С4 ранее) вариантов КИМ ЕГЭ–2017
В планиметрических заданиях заметное структурное и содержательное изменение произошло в 2014 году. В пункте а теперь нужно доказать геометрический факт, в пункте б – найти (вычислить) геометрическую величину.
С точки зрения разработчиков включение проверяемого элемента на доказательство в задание 16 должно повысить уровень подготовки школьников. Кроме того, такое доказательство является естественным продолжением практики использования заданий на доказательство в экзамене за курс основной школы. По фактическим данным выполнения задание 16 является границей, разделяющий высокий и повышенный уровень подготовки участников ЕГЭ.
В 2017 году изменений в структуре и тематическом содержании этих заданий нет.
| Содержание критерия, задание №16 (=18), 2016 г. | Баллы |
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б | |
| Обоснованно получен верный ответ в пункте б ИЛИ имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а, ИЛИ при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Задача 1
|
|
|
Точка 
лежит на отрезке 
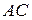. Прямая, проходящая через точку 
, касается окружности с диаметром 
в точке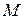 
и второй раз пересекает окружность
с диаметром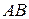 
в точке 
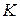. Продолжение отрезка 
пересекает окружность с диаметром 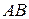в точке 
.
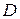а) Докажите, что прямые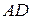 
и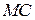 
параллельны.
б) Найдите площадь треугольника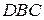 
, есл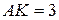и 
и 
.
Решение.
|
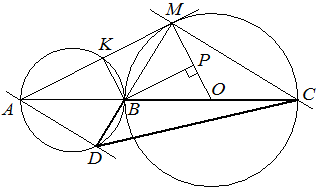
а) Точк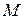и и 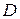лежат на окружностях с диаметрами и 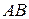соответственно, поэтому
.
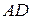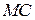Прямые и перпендикулярны одной и той же прямой 
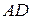, следовательно, прямые и 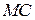параллельны.
б) Пусть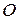 
— центр окружности с диаметром . Тогда прямые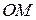 
и 
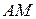перпендикулярны. Учитывая, что прямые 
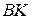и 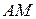перпендикулярны, получаем, что прямые 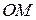и 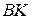параллельны. Обозначим 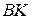через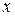 
. Треугольник 
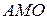подобен треугольнику 
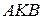с коэффициентом 5, поэтому 
.
Опустим перпендикуляр 
из точки на прямую 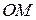. Так как четырёхугольник 
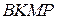— прямоугольник,
, 
.
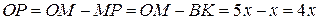По теореме Пифагора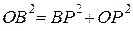 
, откуда 
. Получаем, что 
.
Поскольку прямые 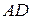и 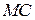параллельны,
.
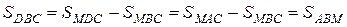Значит, треугольник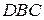и и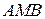 
равновелики. Следовательно,
.
Ответ: б) 30.
Задача 2.
Дан прямоугольный треугольник 
с прямым углом 
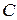. На катете 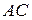взята точка 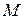. Окружность с центром 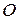и диаметром 
касается гипотенузы в точке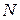 
.
а) Докажите, что прямые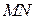 
и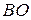 
параллельны.
б) Найдите площадь четырёхугольника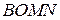 
, есл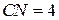и 
и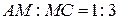 
.
Решение.
|
а) Поскольку прямые 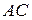и перпендикулярны, прямая — касательная к окружности. По свойству касательных, проведённых к окружности из одной точки, прямая 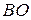перпендикулярна прямой 
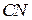. Точка 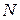лежит
на окружности с диаметром , поэтому 
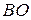. Прямые и 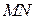перпендикулярны одной и той же прямой 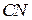, следовательно, они параллельны.
б) Пусть 
, 
. Тогда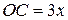 
, 
, 
. Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому 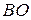— биссектриса треугольника . По свойству биссектрисы
.
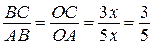Пусть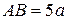 
, 
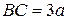. Тогда по теореме Пифагора
.
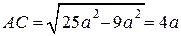Поэтому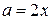 
. Следовательно, 
.
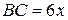Пусть отрезк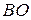и и 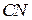пересекаются в точке 
. Тогда — середин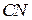а , а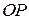 
— средняя линия треугольника 
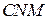. Поскольку 
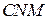, прямоугольные треугольники и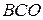 
подобны, откуда
; 
.
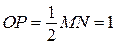Из прямоугольного треугольника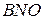 
находим:
; 
.
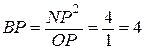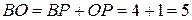По формуле площади трапеции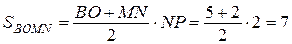 
.
Ответ: б) 7.
Как и во всякой сложной геометрической задаче, весьма деликатным является вопрос о степени и характере обоснованности построений и утверждений. Позиция разработчиков КИМ состоит в том, что при решении задания №16 (=18=С4) невозможно от выпускников школ на экзамене требовать изложения, приближающегося к стилю учебников и методических статей. Достаточным является наличие ясного понимания геометрических конфигураций искомых объектов, верного описания (предъявления) этих конфигураций и грамотно проведённых рассуждений и вычислений. Обратим также внимание на то, что часто при решении геометрических задач школьники ссылаются на весьма невразумительный чертёж, а иногда чертёж вообще отсутствует (если рисунок сделан на бланке карандашом, то эта область не сканируется). Снижать оценку только за это не рекомендуется.
|
|
|
|
|
|
