 |
Оценка эксперта: 0 баллов.
|
|
|
|
6. Критерии проверки и оценка решений заданий 18 (20 в 2015 г., С5 ранее) вариантов КИМ ЕГЭ–2017
Как это обычно бывает, задачи с параметром допускают весьма разнообразные способы решения. Наиболее распространенными из них являются:
– чисто алгебраический способ решения;
– способ решения, основанный на построении и исследовании геометрической модели данной задачи;
– функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.
Зачастую (но далеко не всегда) графический метод более ясно ведёт к цели. Кроме того, в конкретном тексте решения вполне могут встречаться элементы каждого из трех перечисленных способов.
Ниже приведены задачи двух типов из материалов досрочного и основного ЕГЭ–2015, их решения, ответы и соответствующие критерии проверки. Далее в Части 1 приведены 6 примеров решений этих задач на ЕГЭ вместе с комментариями по оценке и самими оценками. Подчеркнём, что каждая задача оценивалась по критериям соответствующего года проведения ЕГЭ.
Задачи типа 1 и 2 имеют много схожего в своей структуре и условиях:
(1) это системы относительно двух переменных;
(2) это системы с параметром;
(3) первое уравнение системы довольно громоздкое, но не содержит параметр;
(4) уравнение, содержащее параметр, напротив, весьма простое; это уравнение пучка параллельных прямых, или прямых, проходящих через фиксированную точку;
(4) всё начинается с преобразований первого уравнения и его решения;
(5) далее, как правило, удобнее использовать геометрическую интерпретацию;
(6) верное выполнение (4) и (5) гарантирует получение 1 балла;
(7) 3 балла выставляется за практически верное решение; допускаются только 1–2 неточности во включении концевых точек соответствующих промежутков;
|
|
|
(8) оценка в 2 балла – самая редкая.
В то же время, имеются и различия. В основном они связаны с видом первого уравнения. В заданиях первого типа эти уравнения сводятся к произведению двух линейных множителей или же линейного множителя и (простейшего) квадратичного множителя. Такое разложение можно провести или группировкой членов, или решая уравнение, как квадратное относительно одной из переменных.
В заданиях второго типа присутствует модуль. При его раскрытии с помощью выделения полных квадратов всё сводится к дугам двух окружностей. Дальнейший существенный шаг состоит в нахождении угловых коэффициентов касательных в точках пересечения этих окружностей. Без знания того, что для наклонных прямых 
(или какого-то аналога нахождения уравнения перпендикуляра к заданной прямой в заданной точке) этот шаг становится почти непреодолимым. Судя по имеющимся сканам работ, верное нахождение угловых коэффициентов касательных в большинстве случаев гарантировало получение 3 баллов за решение.
Задача 1
Найдите все значения 
, при каждом из которых система 
имеет ровно два различных решения.
Решение.
Решим первое уравнение:
.
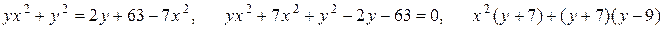
Рассмотрим случай (1): 
. При любом 
получаем одно решение 
, для которого неравенство 
верно только при 
.
Рассмотрим случай (2):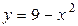 
, 
. Так как 
, то при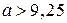 
корней нет, при 
получаем один корень 
, при 
получаем два различных корня. У параболы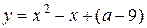 
- ветви вверх, абсцисса вершины равна 
и 
. Значит, оба корня не меньше -3 при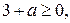 
т.е. при 
, а при 
один корень меньше -3, а другой – больше -3.
Соберем сведения о числе решений в случаях (1) и (2) в таблице
|
| 
| 
|
| 
| 
|
| Число решений (1) | |||||
| Число решений (2) |
Остается учесть те значения , при которых решение из случая (1) совпадает с одним из решений случая (2). Тогда 
, и из 
, получаем, что 
.
|
|
|
Ответ: 
, .
| Содержание критерия, задача №20, ЕГЭ-2015 | Баллы | |
| Обоснованно получен правильный ответ | ||
С помощью верного рассуждения получен ответ, отличающийся от верного на одно или оба из значений  .
| ||
Обоснованно получено, что условие задачи выполняется хотя бы в одном из случаев  или .
| ||
| Задача верно сведена к исследованию расположения парабол и прямых (аналитически или графически) ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения. | ||
| Решение не соответствует ни одному из критериев, перечисленных выше | ||
| Максимальный балл |
Задача 2.
Найдите все значения , при каждом из которых система уравнений
имеет ровно два решения.
Решение.
|
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.
Рассмотрим два случая:
1) Если 
, то получаем уравнение
;
;
.
Полученное уравнение задаёт окружность с центром в точке 
и радиусом 
.
2) Если 
, то получаем уравнение
; 
; 
.
Полученное уравнение задаёт окружность с центром в точке 
и радиусом .
Полученные окружности пересекаются в двух точках 
и 
, лежащих на прямой 
, поэтому в первом случае получаем дугу 
с концами в точках 
и 
, во втором — дугу 
с концами в тех же точках (см. рис.).
Рассмотрим второе уравнение системы. Оно задаёт прямую 
, которая проходит через точку и угловой коэффициент которой равен 
.
При 
прямая проходит через точки и , то есть исходная система имеет два решения.
При 
прямая перпендикулярна прямой 
, угловой коэффициент которой равен 
, значит, прямая касается дуги 
в точке и пересекает дугу 
в двух точках (одна из которых — точка ), то есть исходная система имеет два решения.
При 
прямая перпендикулярна прямой 
, угловой коэффициент которой равен 
, значит, прямая касается дуги в точке
и пересекает дугу в двух точках (одна из которых — точка ), то есть исходная система имеет два решения.
При 
или 
прямая пересекает каждую из дуг и в точке
и ещё в одной точке, отличной от точки , то есть исходная система имеет три решения.
При 
прямая пересекает дугу в двух точках (одна из которых — точка ) и не пересекает дугу в точках, отличных от точки , то есть исходная система имеет два решения.
|
|
|
При 
прямая пересекает дугу в двух точках (одна из которых — точка ) и не пересекает дугу в точках, отличных от точки , то есть исходная система имеет два решения.
Значит, исходная система имеет ровно два решения при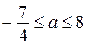 
.
Ответ: .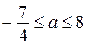
| Содержание критерия, задача №2 | Баллы |
| Обоснованно получен верный ответ | |
С помощью верного рассуждения получено множество значений a, отличающееся от искомого только исключением точек и/или 
| |
| При всех значениях a верно найдено количество решений системы в одном из двух случаев, возникающих при раскрытии модуля | |
| Задача верно сведена к исследованию взаимного расположения дуг окружностей и прямых (аналитически или графически) ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
|
|
|
