 |
Примеры оценивания решений заданий 17
|
|
|
|
Пример 1.
1 июня 2013 года Всеволод Ярославович взял в банке 900 000 рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платёж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300 000 рублей?
Ответ: 4.

Комментарий.
Ответ верен. Более того «…построена математическая модель, решение сведено к исследованию этой модели…», см. критерии; в данном случае – арифметическая, числовая модель. Однако, эта модель построена неверно, т.е. она не соответствует условию. По решению видно, что сначала идет платёж долга, потом – начисление процента, а в условии – наоборот.
Оценка эксперта: 0 баллов.
Пример 2.
1 июня 2013 года Всеволод Ярославович взял в банке 900 000 рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платёж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300 000 рублей?
Ответ: 4.

Комментарий.
Здесь и ответ верен, и движение денег в целом описано верно. К сожалению, в вычислениях есть просчет в первой клетке третьей строки. Добавлен не 1%, а 10%. Эта ошибка «играет» в пользу писавшего, но вычислительная ошибка имеется.
Работает критерий на 2 балла, если в «недостаточно обосновано» включить и случай обоснования с вычислительной ошибкой.
Оценка эксперта: 2 балла.
|
|
|
Пример 3.
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в процентах от кредита) | 100% | 90% | 80% | 70% | 60% | 50% | 0% |
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
Ответ: 22,5.
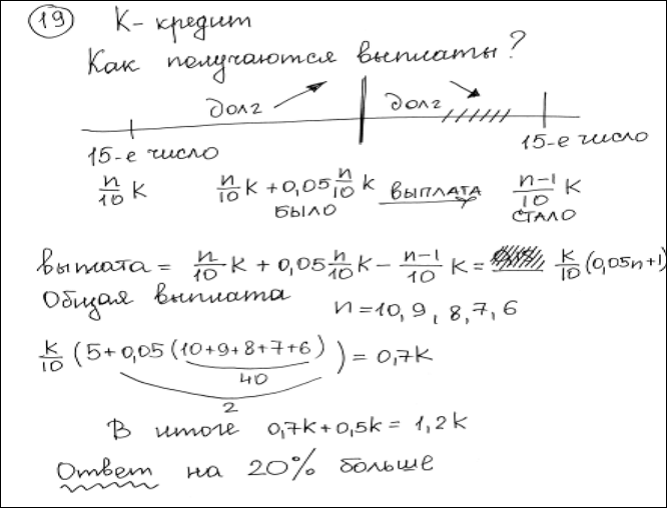
Комментарий.
Почти правильное решение. Есть один обидный (по невнимательности?) прокол: перед выплатой в июле оставшаяся половина долга также увеличивается на 5%
Оценка эксперта: 2 балла.
Пример 4. См. задача 3. Кредит = 28 млн рублей. Рост на 25%. Выплаты равномерные, наибольший платеж 9 млн. Чему будет равна общая сумма выплат после полного погашения кредита?
Ответ: 80,5 млн рублей.
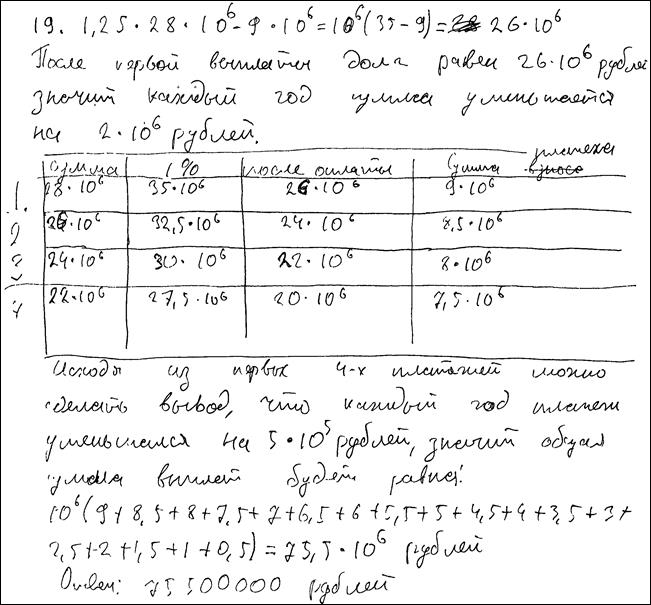
Комментарий.
На беглый взгляд – просто вычислительная ошибка, т.е. 2 балла. Смотрим внимательнее. Первые 4 строки заполнены с пониманием дела, разве что нет обоснования того, что именно первая выплата – наибольшая. В целом, верно описана процедура движения финансов: уменьшение долга, уменьшение размеров выплат. Но, судя по первому столбцу, строчек должно быть 14 (кредит взяли на 14 лет), а у автора, судя по последнему столбцу, их 18. К тому же, есть ошибка в подсчете: 9,5х9 явно больше 75,5.
Оценка эксперта: 1 балл.
Пример 5. См. задача 3. Кредит =9 млн. Рост на 10%. Выплаты равномерные, наибольший платеж 1,5 млн. Чему будет равна общая сумма выплат после полного погашения кредита?
Ответ: 16,2 млн рублей.


Комментарий. Полная и верная бухгалтерская выписка. Можно попробовать «придраться»: а почему именно первая выплата – наибольшая. Но вряд ли возможно снять 1 балл только за это: ведь реализуемость всех условий представлена.
Оценка эксперта: 3 балла.
Пример 6. См. задача 3. Кредит =17 млн. Рост на 10%. Выплаты равномерные, наибольший платеж 3,4 млн. Чему будет равна общая сумма выплат после полного погашения кредита?
|
|
|
Ответ: 26,35 млн рублей.


Комментарий. По внешнему виду – почти то же, что и в Примере 5. Но тут принципиальное непонимание условия: всё время вычитается по 3,4 млн., а в конце – получившийся остаток, меньший 3,4 млн. Скорее всего, автор «переготовился» к ЕГЭ по другой модели «экономической» задачи, с так называемыми «аннуитентными» выплатами.
|
|
|


