 |
Примеры оценивания решений заданий 19
|
|
|
|
Пример 1.
Семь экспертов оценивают кинофильм. Каждый из них выставляет оценку — целое число баллов от 1 до 15 включительно. Известно, что все эксперты выставили различные оценки. По старой системе оценивания рейтинг кинофильма — это среднее арифметическое всех оценок экспертов. По новой системе оценивания рейтинг кинофильма вычисляется следующим образом: отбрасываются наименьшая и наибольшая оценки и подсчитывается среднее арифметическое пяти оставшихся оценок.
а) Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться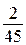 
б) равняться 
?
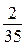в) Найдите наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания.
Комментарий.
В пункте в нет ни примера, ни доказательства, а ответ неверен. В пункте б ответ верен, но примера достижимости таких значений x и y нет. В пункте а ответ верен, верно равенство 45 x = 7(9 y + 2), верно упомянута делимость. Однако, делимость на 7 совершенно не причём! Никакого противоречия нет. Противоречие может быть получено из 45 x – 63 y = 14, т. е. из делимости на 9.
Оценка эксперта: 0 баллов.
Пример 2.
Условие см. выше с числами 1–10, 1/30, 1/35.
Комментарий.
Ответ в пункте б верен, хотя лучше бы не испытывать терпение проверяющего и добавить нужное числовое равенство. В пункте а ответ верен, его обоснование довольно экзотично, но верно.
Оценка эксперта: 2 балла.
Пример 3. Условие см. Пример 1.
Комментарий.
Кристально ясный случай. Приведено доказательство в а и приведены два нужных примера в пунктах б и в. Однако пример в в не обеспечивает «точность предыдущей оценки» так как никакой оценки нет, а есть только эвристическое наблюдение об оценке.
|
|
|
Оценка эксперта: 2 балла.
Пример 4.
а) Приведите пример четырёхзначного числа, произведение цифр которого
в 21 раз больше суммы цифр этого числа.
б) Существует ли такое четырёхзначное число, произведение цифр которого в 245 раз больше суммы цифр этого числа?
в) Найдите все четырёхзначные числа, произведение цифр которых
в 19,6 раза больше суммы цифр этого числа.
Ответ: а) например, 2765; б) нет; в) Число 2477 и все числа, получаемые
из него перестановкой цифр (всего 12 чисел).
Комментарий.
Верное и (слишком) подробное решение. В пункте а хватило бы только одного примера, а сейчас там полный перебор всех вариантов. В пункте б решение «лучше», чем предложенное автором задачи. В пункте в автор несколько рисковал, явно перечисляя все 12 вариантов: если бы он один из них пропустил, то пришлось бы обсуждать оценку в 3 балла.
Оценка эксперта: 4 балла.
Пример 5. См. Пример 4.
Комментарий.
Обоснованно получен ответ в п. б. Неверно решен п. а. П в. решен по существу верно, но при перечислении вариантов пропущены два числа. Типичный неприятный случай: формально, по критериям лучше, чем на 1 балл, но несколько хуже, чем на 2 балла. При этом если совсем «простить» перечислительный просчет, то можно говорить и о 3 баллах.
Оценка эксперта: 2 балла.
Пример 6.
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы
в каждой группе было хотя бы одночисло. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы
из единственного числа среднее арифметическое равно этому числу).
а) Могут ли быть одинаковыми два из этих трёх значений средних арифметических в группах из разного количества чисел?
б) Могут ли быть одинаковыми все три значения средних арифметических?
в) Найдите наименьшее возможное значение наибольшего из получаемых трёх средних арифметических.
|
|
|
Ответ: а) да; б) нет; в) 
.
Комментарий.
Скорее всего, автор был близок к верному решению. Но в решении пункта а пропустил условие «…из разного количества чисел», а в пункте в поторопился с ответом, не попытавшись привести пример его реализуемости. Обоснование в б, быть может, не идеально, но оно по существу верно.
Оценка эксперта: 1 балл.
|
|
|
