 |
Предмет теории вероятностей
|
|
|
|
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
ЭКОНОМИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ ВСЕХ ФОРМ ОБУЧЕНИЯ
СИМФЕРОПОЛЬ
2006 г.
УДК – 51
ББК – 32.17
А – 44
Акульшина Т.С., Стебко Т.В. Теория вероятностей и математическая статистика. Методические указания и контрольные задания. Для самостоятельной работы студентов экономических специальностей всех форм обучения. – Симферополь: УЭУ, 2006 – 62 с.
Методические указания разработаны в помощь студентам всех экономических специальностей при изучении теоретического материала и выполнении самостоятельных, практических и контрольных работ по курсу «Теория вероятностей и математическая статистика». Включают в себя основные понятия и формулы теории вероятностей и математической статистики. Содержат разобранные задачи по различным темам дисциплины, а также ряд задач для самостоятельного решения.
© Симферополь, 2006.
I. ПРОГРАММА КУРСА
«ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
Раздел I. Теория вероятностей.
Тема 1. Основные понятия теории вероятностей. Предмет курса.
Предмет курса, его содержание. Роль и место курса как теоретической базы вероятностно - статистического моделирования, основ курсов "Математическое программирование", "Эконометрия", "Экономический риск и методы его измерения" и др.
Классификация событий: достоверные, невозможные, случайные. Понятия элементарных и сложных случайных событий, простор элементарных событий; операции над событиями. Классическое определение вероятности случайного события. Элементы комбинаторики в теории вероятностей и следствия из них; геометрическая вероятность, статистическая вероятность.
|
|
|
Тема 2. Зависимые и независимые случайные события. Основные формулы умножения и сложения вероятностей.
Понятия зависимых и независимых случайных событий. Условная вероятность и ее особенности. Формулы умножения вероятностей для зависимых и независимых случайных событий. Использование формул умножения вероятностей для оценки надежности систем. Формула полной вероятности. Формула Бейеса.
Тема 3. Повторные независимые испытания по схеме Бернулли.
Определение повторных независимых испытаний. Формула Бернулли для вычисления вероятности и наивероятнейшего числа. Асимптотические формулы для формулы Бернулли (локальная и интегральная теоремы Муавра - Лапласа). Использование интегральной теоремы. Формула Пуассона для маловероятных случайных событий.
Тема 4. Одномерные случайные величины и их характеристики.
Определение случайной величины. Дискретные и непрерывные случайные величины и их законы распределения. Функция распределения вероятностей, ее свойства. Числовые характеристики случайных величин: математическое ожидание, дисперсия и их свойства, среднее квадратическое отклонение, мода, медиана, начальные и центральные моменты, асимметрия и эксцесс. Числовые характеристики среднего арифметического n независимых случайных величин.
Тема 5. Многомерные случайные величины и их свойства.
Определение многомерной случайной величины и ее закон распределения. Система двух дискретных случайных величин, числовые характеристики системы, корреляционный момент, коэффициент корреляции и его свойства. Функция распределения вероятностей, ее свойства. Числовые характеристики системы двух непрерывных случайных величин. Условные законы распределения и их числовые характеристики. Определение корреляционной зависимости. Система n случайных величин, числовые характеристики системы, корреляционная матрица, нормированная корреляционная матрица.
|
|
|
Тема 6. Функции случайных величин.
Определение функции случайных величин. Функция дискретного случайного аргумента и ее числовые характеристики. Функция непрерывного случайного аргумента и ее числовые характеристики. Функции двух случайных аргументов. Определение функции распределения вероятностей для функции двух случайных аргументов.
Тема 7. Основные законы распределения целочисленных случайных величин.
Определение целочисленной случайной величины. Биноминальный, пуассоновский, геометрический и равномерный законы распределения, функции и числовые характеристики для этих законов. Гипергеометрический закон.
Тема 8. Основные законы распределения непрерывных случайных величин.
Определение характеристической функции и ее использование в теории вероятностей. Нормальный закон распределения и его значение в теории вероятностей. Логарифмический нормальный закон. Гамма - распределение. Экспоненциальный закон и его использование в теории надежности, теории очередей. Распределение Вейбула. Равномерный закон. Распределение 
. Распределение 
. Распределение Стьюдента. Распределение Фишера.
Тема 9. Предельные теоремы теории вероятностей.
Неравенство Чебышева и его значение. Теорема Чебышева. Теорема Бернулли. Центральная предельная теорема теории вероятностей (теорема Ляпунова) и ее использование в математической статистике.
Тема 10. Элементы теории случайных процессов.
Определение случайного процесса и классификация случайных процессов. Законы распределения и основные характеристики. Поток событий и свойства. Поток событий Пальма. Пуассоновский поток и его свойства. Формула Пуассона для наипростейшего потока (потока Пуассона). Поток Эрланга. Марковские процессы. Цепи Маркова с дискретными состояниями. Однородные Марковские цепи и их классификация. Стационарные вероятности для регулярных цепей Маркова. Использование однородных цепей Маркова для оценки эффективности функционирования систем. Элементы теории массового обслуживания (теории очередей). Математическая модель для наипростейшей системы обслуживания.
|
|
|
Раздел II. Математическая статистика.
Тема 11. Элементы математической статистики. Выборочный метод.
Генеральная и выборочная совокупности. Статистическое распределение выборки. Гистограмма и полигон статистических распределений. Числовые характеристики: выборочная средняя, дисперсия выборки, среднее квадратичное отклонение, мода и медиана, для дискретных и интервальных статистических распределений выборки, эмпирические начальные и центральные моменты, асимметрия и эксцесс.
Тема 12. Статистические оценки параметров генеральной совокупности. Статистические гипотезы.
Определение статистической оценки. Точечные статистические оценки: смещенные и несмещенные, эффективные и состоятельные. Точечные несмещенные статистические оценки для генеральной средней и генеральной дисперсии, исправленная дисперсия. Интервальные статистические оценки. Точность и надежность оценки, определение доверительного интервала. Построение доверительных интервалов для генеральной средней с известным и неизвестным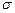 
. Построение доверительных интервалов для генеральной дисперсии и генерального среднего квадратичного отклонения. Определение статистической гипотезы. Нулевая и альтернативная, простая и сложная. Ошибки первого и второго рода. Статистический критерий. Критическая область, область принятия нулевой гипотезы, критическая точка. Методика построения правосторонней, левосторонней и двусторонней критических областей. Проверка правдивости нулевой гипотезы нормального закона распределения. Признаки генеральной совокупности. Проверка статистических гипотез про равенство двух генеральных средних и двух дисперсий, признаки которых имеют нормальные законы распределения. Эмпирическая и теоретическая частоты. Критерий согласия Пирсона. Критерий согласия Смирнова.
Тема 13. Элементы дисперсионного анализа.
Модель эксперимента. Однофакторный анализ. Таблица результатов наблюдений. Общая дисперсия, межгрупповая и внутригрупповая дисперсии. Оценки дисперсий. Общий метод проверки влияния фактора на признак способом сравнения дисперсий. Понятие о двухфакторном дисперсионном анализе.
|
|
|
Тема 14. Элементы теории регрессии и корреляции.
Функциональная, статистическая и корреляционная зависимости. Уравнение парной регрессии. Свойства статистических оценок параметров парной функции регрессии. Выборочный коэффициент корреляции и его свойства. Доверительный интервал для линии регрессии. Коэффициент детерминации. Множественная регрессия, определение статистических оценок для параметров линейной множественной функции регрессии. Коэффициент корреляции и его свойства. Нелинейная регрессия. Определение статистических оценок для нелинейной функции регрессии.
II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПРЕДМЕТ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Всякое действие, явление, реализуемое при определенном комплексе условий, называют испытанием.
Результат испытания называют событием.
Пример. Брошена монета – испытание;
Появление герба – событие.
События обозначают заглавными буквами латинского алфавита: А, В, …
Наблюдаемые нами события можно подразделить на следующие три вида:
q Достоверные;
q Невозможные;
q Случайные;
Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S.
Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий S.
Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти.
Пример. Брошена игральная кость – испытание;
Выпадение 4 х очков – событие; какое? – случайное;
Выпадение не больше 6 и очков – событие; какое? – достоверное;
Выпадение 10 и очков – событие; какое? – невозможное.
Каждое случайное событие, в частности – выпадение герба, есть следствие действия очень многих случайных причин (сила, с которой брошена монета, форма монеты, сплав, из которого она сделана, и др.). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет, – она просто не в силах это сделать.
По-иному обстоит дело, если рассматриваются случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий S, т.е. если речь идет о массовых однородных случайных событиях. Оказывается, что достаточно большое число однородных случайных событий, независимо от их конкретной природы, подчиняется определенным закономерностям, а именно – вероятностным закономерностям. Установлением этих закономерностей и занимается теория вероятностей.
|
|
|
Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.
Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать.
Например, нельзя наперед определить результат одного бросания монеты, но можно предсказать, причем с небольшой погрешностью, число появлений герба, если монета будет брошена достаточно большое число раз. При этом предполагается, конечно, что монета бросается в одних и тех же условиях.
Например, то, что застрахованный объект (дом, домашнее имущество и т.п.) будет уничтожен в результате стихийного бедствия, – дело случая. Чем же тогда страховые органы руководствуются в своей работе? Оказывается, что если о будущем определенного застрахованного объекта сказать ничего нельзя, то о состоянии большого их числа можно почти наверняка сказать многое.
ВИДЫ СЛУЧАЙНЫХ СОБЫТИЙ
События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Пример. Монета брошена 1 раз. События: А – выпал герб и В – выпала решка несовместные.
Брошена игральная кость. События: А – выпала 1, В – выпала 2, С – выпала 3 несовместные.
События называют совместными, если появление одного из них не исключает появление других событий в одном и том же испытании.
Пример. Брошены две игральные кости. События: А – выпала 4 на первой кости, событие В – выпала 5 на второй кости совместные.
События называют единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием.
Пример. Стрелок произвел выстрел по цели. События: А – попадание в цель, В – промах единственно возможные в данном испытании.
События называют равновозможными, если есть основание считать, что ни одно из этих событий не является более возможным, чем другие.
Пример. Брошена игральная кость. Равновозможные события: А – выпала 3 и В – выпала 5; или С – выпало четное число и D – выпало нечетное число очков.
Совокупность всех единственно возможных событий испытания называют полной группой событий.
Пример. Стрелок произвел 2 выстрела.
Полная группа событий: 
; где
Событие 
– промах;
Событие 
– одно попадание;
Событие 
– два попадания;
Противоположными называют два единственно возможных события, образующих полную группу событий.
Обозначение: 
и 
;
Пример. Монета брошена 1 раз. События: – выпал герб и – выпала решка противоположные.
Брошена игральная кость. События: – выпало четное число очков и – выпало нечетное число очков противоположные.
События: – выпала 1 и – не выпала 1 противоположные.
ОПЕРАЦИИ НАД СОБЫТИЯМИ
Суммой конечного числа событий называют новое событие, состоящее в наступлении хотя бы одного из них.
(Суммой событий А и В называют событие, состоящее в появлении, или события А, или события В, или обоих событий.);
Логический принцип: или – или.
Обозначение: А+В
Пример. Событие А – попадание в круг, а событие В – попадание в квадрат;
Тогда их сумма А+В заключается в попадании или в круг, или в квадрат.
Произведением конечного числа событий называют новое событие, состоящее в том, что произойдут все эти события.
(Произведением двух событий А и В называют событие, состоящее и в появлении события А, и в появлении события В).
Логический принцип и – и.
Обозначение: А∙В
Пример. Событие А – попадание в круг, а событие В – попадание в квадрат;
Тогда их произведение А∙В заключается в попадании в общую часть круга и квадрата.
|
|
|
