Тема: Теоремы сложения и умножения вероятностей

Вам предлагается 5 тестовых заданий по теме: «Теоремы сложения и умножения вероятностей». Среди предлагаемых вариантов ответов только один является верным. Выберите верный ответ на вопрос или верное продолжение фразы и соответствующие им буквы запишите в листок ответа.

№	Задание	Предлагаемые варианты ответов
1.	Событие, состоящее в том, что произойдет либо событие А, либо событие В, можно обозначить:	a) А–В; b) А+В; c) А×В; d) РА(В).
2.	Формула Р(А+В) = Р(А) + Р(В) соответствует теореме сложения вероятностей:	a) зависимых событий; b) независимых событий; c) совместных событий; d) несовместных событий.
3.	Вероятность промаха для торпедного катера равна 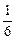. Катер произвел 6 выстрелов. Вероятность того, что все 6 раз катер попал в цель, равна:	a) 1; b) ; c) ; d) .
4.	Вероятность совместного появления событий А и В обозначают:	a) Р(А×В); b) Р(А+В); c) РВ(А); d) РА(В).
5.	Дана задача: в первом ящике – 5 белых и 3 красных шара, во втором – 3 белых и 10 красных шаров. Из каждого ящика наудачу взяли по одному шару. Определить вероятность того, что оба шара одного цвета. Для решения задачи используют:	a) Теорему умножения вероятностей несовместных событий и теорему сложения вероятностей независимых событий; b) Теорему сложения вероятностей несовместных событий; c) Теорему умножения вероятностей независимых событий и теорему сложения вероятностей несовместных событий; d) Теорему умножения вероятностей зависимых событий.

ТЕСТ №3

Тема: Случайные независимые испытания по схеме Бернулли

Вам предлагается 5 тестовых заданий по теме: «Случайные независимые испытания по схеме Бернулли». Среди предлагаемых вариантов ответов только один является верным. Выберите верный ответ на вопрос или верное продолжение фразы и соответствующие им буквы запишите в листок ответа.

№	Задание	Предлагаемые варианты ответов
1.	Дана задача: Вероятность того, что на странице студенческого реферата есть опечатка, равна 0,03. Реферат состоит из 8 страниц. Определить вероятность того, что ровно 5 из них с опечаткой. Для решения этой задачи используют:	a) Формулу Бернулли; b) Локальную теорему Лапласа; c) Интегральную теорему Лапласа; d) Формулу Пуассона.
2.	В семье планируют завести 5 детей. Если считать вероятность рождения мальчика 0,515, то –наивероятнейшее число девочек в семье равно:	a) 1; b) 2; c) 3; d) 4.
3.	Имеется группа, состоящая из 500 человек. Найти вероятность того, что у двух человек день рождения придется на Новый год. Считать, что вероятность рождения в фиксированный день равна . Для решения этой задачи используют:	a) Формулу Бернулли; b) Локальную теорему Лапласа; c) Интегральную теорему Лапласа; d) Формулу Пуассона.
4.	Для определения вероятности того, что в 300 испытаниях событие А произойдет не менее 40 раз, если вероятность А в каждом испытании постоянна и равна 0,15, используют:	a) Формулу Бернулли и теорему сложения вероятностей несовместных событий; b) Локальную теорему Лапласа; c) Интегральную теорему Лапласа; d) Формулу Пуассона, теорему сложения вероятностей несовместных событий, свойство вероятностей противоположных событий.
5.	Дана задача: известно, что в некоторой местности в сентябре бывает 18 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце семи дней два дня окажутся дождливыми? Для решения этой задачи используют:	a) Формулу Бернулли; b) Локальную теорему Лапласа; c) Интегральную теорему Лапласа; d) Формулу Пуассона.

ТЕСТ №4