Случайные величины и законы их распределения

Случайная величина – это такая величина, которая в результате опыта может принять то или иное значение из некоторого числового множества, однако заранее неизвестно, какое именно. Случайную величину обозначают большими буквами латинского алфавита X, Y, Z, …, а ее возможные значения – соответствующими малыми буквами x, y, z, ….

Различают дискретные (прерывные) и непрерывные случайные величины.

Дискретной случайной величиной (ДСВ) называют такую величину, все возможные значения которой являются изолированными числами.

Непрерывной случайной величиной (НСВ) называют величину, все возможные значения которой заполняют конечный или бесконечный промежуток на числовой оси.

Каждому значению дискретной величины соответствует определенная вероятность .

Каждому промежутку 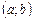из области значений непрерывной случайной величины также соответствует вероятность того, что значение, принятое случайной величиной, попадет в этот промежуток.

Законом распределения случайной величины называют соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Дискретную случайную величину можно задать:

1) в виде таблицы, которую называют рядом распределения. Первая строка таблицы содержит возможные значения 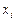, а вторая вероятности :

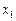
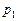
где ;

2) в виде графика; строят точки с координатами , откладывая по оси абсцисс 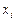, а по оси ординат – , и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Закон распределения непрерывной случайной величины задается или интегральной функцией распределения , или плотностью распределения 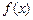(дифференциальной функцией).

Интегральной функцией распределения называют функцию , определяющую для каждого значения 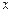вероятность того, что случайная величина примет значение, меньшее 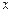, т.е.

.

Примечание. Дискретную случайную величину можно также задавать интегральной функцией. Ее график представляет собой ступенчатую фигуру.

Интегральная функция обладает следующими свойствами:

Свойство 1. Значения интегральной функции принадлежат отрезку :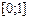

.

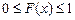Свойство 2. Интегральная функция есть неубывающая функция, т.е.

, если .

Следствие. Вероятность того, что случайная величина примет значение, заключенное в интервале 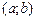, равна приращению интегральной функции на этом интервале:

.

Дифференциальной функцией распределения вероятностей называют первую производную от интегральной функции:

.

Примечание. Для дискретной случайной величины эта функция не применима.

Зная дифференциальную функцию, можно найти интегральную функцию по формуле:

.

Пример. Дискретная случайная величина задана рядом распределения.

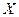
	–1			2,5
	0,2	0,3	0,4	0,1

Построить многоугольник распределения, функцию распределения и ее график.

Решение. Строим многоугольник распределения (рис.1):

Найдем интегральную функцию.

Если , то = 0.

Если , то .

Если , то .

Если , то .

Если , то , т.к. событие достоверное и его вероятность равна единице.

Таким образом, интегральная функция аналитически может быть записана так:

График этой функции имеет вид, представленный на рис.2:

В каждой точке 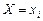функция имеет скачок, величина которого равна вероятности .

Пример. Дана дифференциальная функция непрерывной случайной величины :

Найти: а) интегральную функцию и построить ее график;

б) вероятность того, что в результате испытания примет значение, принадлежащее интервалу .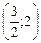

Решение. а) Воспользуемся формулой .

Если 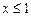, то , следовательно, .

Если , то .

Если , то .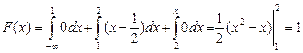

Итак, искомая интегральная функция имеет вид:

График этой функции приведен на рис.3.

б) Воспользуемся формулой .

По условию . Следовательно, искомая вероятность:

.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: