 |
Испытания по схеме Бернулли
|
|
|
|
На практике приходится сталкиваться с такими задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появится событие  . При этом интерес представляет исход не каждого отдельного испытания, а общее количество появлений события
. При этом интерес представляет исход не каждого отдельного испытания, а общее количество появлений события  в результате определенного количества испытаний.
в результате определенного количества испытаний.
Испытания называют повторно независимыми, если испытания являются независимыми и вероятность появления события  в каждом испытании постоянна.
в каждом испытании постоянна.
Повторяющиеся испытания, удовлетворяющие условию независимости и постоянства вероятностей появления в каждом из них события  , называют испытаниями Бернулли, или схемой Бернулли.
, называют испытаниями Бернулли, или схемой Бернулли.
Пусть производится  независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события  постоянна и равна
постоянна и равна  . Требуется найти вероятность
. Требуется найти вероятность  того, что при
того, что при  повторных испытаниях событие
повторных испытаниях событие  произойдет
произойдет  раз.
раз.
В зависимости от значений  и
и  задача предложенного типа решается по различным формулам.
задача предложенного типа решается по различным формулам.
· Если  , то используют формулу Бернулли:
, то используют формулу Бернулли:
 ,
,
где  –вероятность ненаступления события
–вероятность ненаступления события  в каждом испытании.
в каждом испытании.
· Если  и
и  , то используют локальную теорему Лапласа:
, то используют локальную теорему Лапласа:
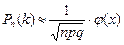 ,
,
где  ,
, 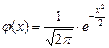 .
.
Значения  находят по таблице приложения 1. Функция
находят по таблице приложения 1. Функция  четная, т.е.
четная, т.е.  , таблица содержит значения функции
, таблица содержит значения функции  лишь для
лишь для  ; при
; при 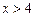 можно принять
можно принять  .
.
· Если  и
и 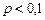 , (либо
, (либо  ), то используют формулу Пуассона:
), то используют формулу Пуассона:
 ,
,
где  ;
;  .
.
Пример. Вероятность появления события  в каждом из 7 независимых испытаний постоянна и равна
в каждом из 7 независимых испытаний постоянна и равна  . Определить вероятность того, что:
. Определить вероятность того, что:
1) Событие  наступит ровно 5 раз;
наступит ровно 5 раз;
2) Событие  наступит не менее 5 раз.
наступит не менее 5 раз.
Решение. По условию  ;
;  . Т.о. для решения задачи используют формулу Бернулли.
. Т.о. для решения задачи используют формулу Бернулли.
1) Вероятность того, что событие  наступит 5 раз:
наступит 5 раз:  ;
;  .
.
|
|
|
Искомая вероятность:
 .
.
2) Событие  наступит не менее 5 раз (следовательно, событие
наступит не менее 5 раз (следовательно, событие  наступит или 5 раз, или 6 раз, или 7 раз). Используем теорему сложения вероятностей несовместных событий и формулу Бернулли:
наступит или 5 раз, или 6 раз, или 7 раз). Используем теорему сложения вероятностей несовместных событий и формулу Бернулли:
 .
.
 ;
;
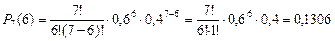 ;
;
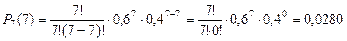 .
.
Искомая вероятность:
 .
.
Пример. Процент всхожести семян  . Определить вероятность того, что из 1000 посеянных семян взойдут 780,
. Определить вероятность того, что из 1000 посеянных семян взойдут 780,
Решение. Т.к. процент всхожести семян  , то вероятность взойти для каждого семени постоянна и равна
, то вероятность взойти для каждого семени постоянна и равна 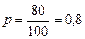 . Количество посеянных семян (общее количество испытаний)
. Количество посеянных семян (общее количество испытаний)  . Т.к.
. Т.к.  и
и  , то используем локальную теорему Лапласа:
, то используем локальную теорему Лапласа:
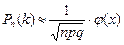 , где
, где  ;
;
 ;
;  .
.
Откуда 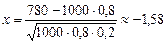 .
.
По таблице значений функции  (приложение 1), учитывая четность функции, найдем:
(приложение 1), учитывая четность функции, найдем:
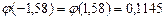 .
.
Искомая вероятность:
 .
.
Пример. Вероятность того, что станок изготовит бракованное изделие, постоянна и равна  . Найти вероятность того, что из 400 произведенных станком изделий:
. Найти вероятность того, что из 400 произведенных станком изделий:
1) ровно 3 бракованных;
2) не менее 3 бракованных.
Решение. Вероятность изготовления бракованного изделия постоянна и равна  . Общее количество изготовленных изделий (общее количество испытаний)
. Общее количество изготовленных изделий (общее количество испытаний)  . Т.к.
. Т.к.  и
и 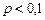 , то используем формулу Пуассона:
, то используем формулу Пуассона:
 , где
, где  .
.
1) Среди изготовленных изделий ровно 3 бракованных:  ;
;
 .
.
Искомая вероятность:
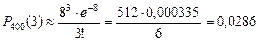 .
.
2) Для определения вероятности того, что среди изготовленных деталей не менее 3 бракованных, целесообразно найти вероятность противоположного события: среди изготовленных деталей меньше 3 бракованных.
 .
.
Событию, среди изготовленных деталей меньше 3 бракованных, благоприятны исходы: 0 бракованных деталей, или 1 бракованная деталь, или 2 бракованных детали.
Используя теорему сложения вероятностей несовместных событий и формулу Пуассона, найдем вероятность того, что среди изготовленных деталей меньше 3 бракованных:
 .
.
 ;
;
 ;
;
 .
.
Следовательно,
 .
.
Искомая вероятность:
 .
.
Наивероятнейшим числом появления события  в
в  независимых испытаниях называют такое число
независимых испытаниях называют такое число  , для которого вероятность, соответствующая этому числу, превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных чисел появления события
, для которого вероятность, соответствующая этому числу, превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных чисел появления события  .
.
|
|
|
Для определения наивероятнейшего числа не обязательно вычислять вероятности возможных чисел появлений события, достаточно знать число испытаний  и вероятность появления события
и вероятность появления события  в отдельном испытании.
в отдельном испытании.
Для определения наивероятнейшего числа используют двойное неравенство:
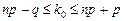 .
.
Следует иметь в виду, что:
1) если 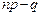 – целое число, то существуют два значения наивероятнейшего числа, а именно:
– целое число, то существуют два значения наивероятнейшего числа, а именно:  и
и  ;
;
2) если 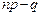 – дробное число, то существует одно наивероятнейшее число, а именно: единственное целое, заключенное между дробными числами, полученными из неравенства;
– дробное число, то существует одно наивероятнейшее число, а именно: единственное целое, заключенное между дробными числами, полученными из неравенства;
3) если 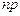 – целое число, то существует одно наивероятнейшее число, а именно:
– целое число, то существует одно наивероятнейшее число, а именно:  .
.
Пример. Определить наивероятнейшее число качественных изделий в партии из 300 изделий, если вероятность качественного изделия равна  .
.
Решение. По условию  ,
,  ; следовательно
; следовательно  .
.
Используя неравенство:
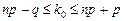 ,
,
имеем
 ;
;
откуда
 .
.
Следовательно, наивероятнейшее число качественных изделий в партии из 300 изделий равно 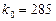 .
.
Предположим, что проводится  независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события  постоянна и равна
постоянна и равна  . Требуется найти вероятность
. Требуется найти вероятность  того, что при
того, что при  повторных испытаниях событие
повторных испытаниях событие  произойдет не менее
произойдет не менее  раз и не более
раз и не более 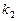 раз. Это можно сделать с помощью интегральной теоремы Лапласа:
раз. Это можно сделать с помощью интегральной теоремы Лапласа:
 ,
,
где  ,
,  ;
;
 . Значения
. Значения  находят по таблице приложения 2. Функция
находят по таблице приложения 2. Функция  нечетная, т.е.
нечетная, т.е. 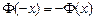 , таблица содержит значения функции
, таблица содержит значения функции  лишь для
лишь для  ; для
; для 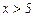 можно принять
можно принять  .
.
Пример. Вероятность того, что деталь изготовлена с нарушениями стандартов, равна  . Найти вероятность того, что среди 800 случайно отобранных деталей нестандартных окажется от 140 до 200 деталей.
. Найти вероятность того, что среди 800 случайно отобранных деталей нестандартных окажется от 140 до 200 деталей.
Решение. По условию  ,
,  ,
,  ,
,  , следовательно,
, следовательно,  .
.
Воспользуемся интегральной теоремой Лапласа:
 , где
, где  ,
,  ;
;
найдем
 ;
;
 .
.
По таблице значений функции  (приложение 2), учитывая нечетность функции, найдем:
(приложение 2), учитывая нечетность функции, найдем:
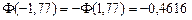 ;
;
 .
.
Искомая вероятность:
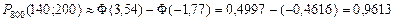 .
.
|
|
|


