 |
Элементы математической статистики
|
|
|
|
Выборочной совокупностью, или просто выборкой, называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Объемом совокупности (выборочной или генеральной) называют число объектов, из которых производится выборка.
Пусть для изучения количественного (дискретного или непрерывного) признака 
из генеральной совокупности извлечена выборка 
объема 
, причем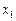 
наблюдалось 
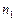раз, 
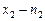раз,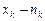 
раз и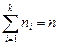 
. Наблюдаемые значения 
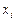называют вариантами, а последовательность вариант, записанных в порядке возрастания, – вариационным рядом.
Числа наблюдений ;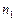 
; …; 
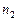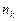называют частотами, а их отношения к объему выборки 
– относительными частотами.
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот (в теории вероятностей – ряд распределения). Статистическое распределение можно задавать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
Полигоном частот называют ломаную, отрезки которой соединяют точки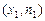 
, 
, …, 
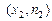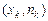, где 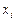–варианты выборки и 
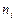– соответствующие им частоты (в теории вероятностей – многоугольник распределения).
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки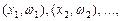 
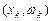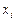, где –варианты выборки и 
– соответствующие им относительные частоты.
Пример. Построить полигон относительных частот по данному распределению выборки:
|
| |||
|
|
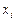
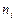
Решение. Найдем объем выборки:
,
.
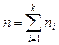Найдем относительные частоты, для чего разделим частоты на объем выборки:
|
|
|
.
Запишем распределение относительных частот:
|
| |||
|
| 
| 
| 
|
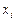
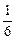
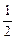
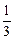
Контроль: 
.
 |
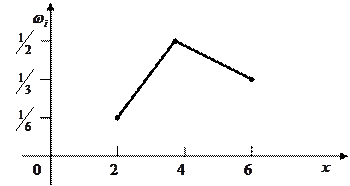Отложим на оси абсцисс варианты
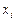, а на оси ординат – соответствующие им относительные частоты . Соединив точки 
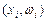отрезками прямых, получим искомый полигон относительных частот, рис.6:
Рис.6
Эмпирической функцией распределения называют функцию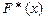 
, определяющую для каждого значения 
относительную частоту события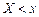 
:
,
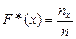где 
– число вариант, меньших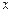 
.
Эмпирическая функция обладает следующими свойствами:
Свойство 1. Значения эмпирической функции принадлежат отрезку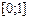 
;
Свойство 2. 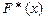– неубывающая функция;
Свойство 3. Если 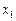– наименьшая варианта, а 
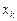– наибольшая, то 
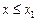при 
и 
при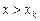 
.
Пример. Найти эмпирическую функцию по данному распределению выборки:
|
| |||
|
|
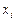
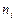
и построить ее график.
Решение. Найдем объем выборки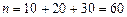 
.
Наименьшая варианта равна единице, следовательно,
при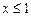 
.
Значение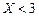 
, а именно 
, наблюдалось 
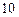раз, следовательно,
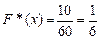при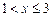 
.
Значения 
, а именно и 
, наблюдались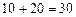 
раз, следовательно,
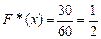при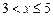 
.
Так как 
наибольшая варианта, то
при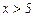 
.
Напишем искомую эмпирическую функцию:
 |
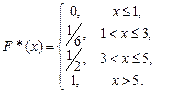
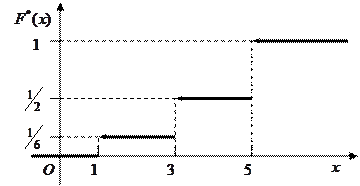График этой функции изображен на рис.7.
Рис. 7
Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение.
Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Статистические оценки могут быть точечные и интервальные.
Точечной называют статистическую оценку, которая определяется одним числом. Интервальной называют статистическую оценку, которая определяется двумя числами – концами интервала.
Точечная оценка может быть несмещенной, т.е. ее математическое ожидание должно быть равно оцениваемому параметру при любом объеме выборки.
|
|
|
Несмещенной оценкой генеральной средней служит выборочная средняя
,
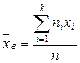где 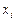– варианта выборки, 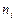– частота варианты , 
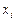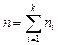– объем выборки.
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия
.
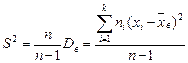Пример. Из генеральной совокупности извлечена выборка:
|
| ||||
|
|
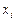
Найти несмещенные оценки генеральной средней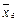 
и генеральной дисперсии 
.
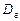Решение. Несмещенной оценкой генеральной средней является выборочная средняя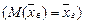 
.
.
Найдем исправленную выборочную дисперсию:
.
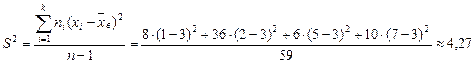Модой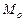 
называют варианту, которая имеет наибольшую частоту.
Например, для ряда
|
| ||||
|
|
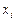
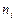
мода равна 5.
Медианой 
называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т.е. 
, то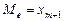 
; при четном 
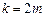медиана 
.
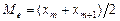Например, для ряда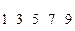 
медиана равна 5; для ряда 
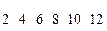медиана равна 
.
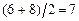Размахом варьирования 
называют разность между наибольшей и наименьшей вариан-тами:
.
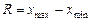Например, для ряда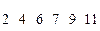 
размах равен 
.
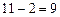Доверительным называют интервал, который с заданной надежностью 
покрывает оцениваемый параметр.
Для оценки математического ожидания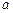 
нормально распределенного количественного признака по выборочной средней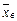 
при известном среднем квадратическом отклонении 
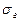генеральной совокупности служит доверительный интервал
,
где 
– точность оценки; – объем выборки; 
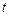есть такое значение аргумента функции Лапласа 
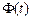(приложение 1), при котором 
.
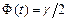Пример. Найти доверительный интервал для оценки с надежностью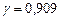 
неизвестного математического ожидания 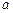нормально распределенного признака генеральной совокупности, если даны генеральное среднее квадратическое отклонение 
, выборочная средняя 
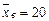и объем выборки 
.
Решение. Требуется найти доверительный интервал
.
Здесь все величины, кроме 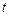, известны. Найдем 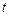. Из соотношения 
получим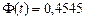 
. По таблице (приложение1) находим 
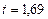. Подставив в формулу для нахождения доверительного интервала соответствующие знаения 
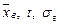и , получим искомый доверительный интервал 
.
III. КОНТРОЛЬНЫЕ ЗАДАНИЯ
Задание 1. Классическое определение вероятности
|
|
|
1. В отделе работают 7 мужчин и 3 женщины. В командировку отобраны 5 человек. Определить вероятность того, что среди них две женщины.
2. Из шести карточек с буквами И К С Т У Э наугад одну за другой выбирают четыре карточки и располагают в ряд в порядке появления. Какова вероятность того, что получится слово «СТУК»?
3. Совет директоров состоит из трех бухгалтеров и четырех менеджеров. Планируется создать подкомитет из его членов. Какова вероятность того, что все трое в подкомитете будут менеджеры.
4. На складе имеется 15 телевизоров, причем 10 из них изготовлены Симферопольским заводом «Фотон». Найти вероятность, что среди четырех выбранных наудачу телевизоров, нет изготовленных в Симферополе.
5. В папке 10 квитанций, три из которых заполнены неверно. Наудачу извлечены 6 квитанций. Найти вероятность того, что среди извлеченных – две квитанции заполнены неверно.
6. В группе 13 студентов, среди которых 5 отличников. По списку наудачу отобраны 8 студентов. Найти вероятность того, что среди них трое отличников.
7. В компьютерном классе 10 машин, 7 из которых подключены к сети Internet. Наудачу выбраны три машины. Найти вероятность того, что одна из них подключена к сети Internet.
8. Устройство содержит 7 элементов, из которых три изношенные. При включении устройства включаются случайным образом три элемента. Найти вероятность того, что включенными окажутся два изношенных элемента.
9. В ящике содержится 10 деталей, из них 4 бракованные. Наудачу извлечены три детали. Найти вероятность того, что среди извлеченных только одна бракованная.
10. Набирая номер телефона, абонент забыл три последние цифры и, помня лишь, что эти цифры разные, набрал их наугад. Найти вероятность того, что набраны нужные цифры.
11. В чемпионате института по футболу участвуют 6 команд, 4 из которых представляют факультет экономики. Для жеребьевки декан пригласил трех капитанов команд. Какова вероятность того, что все они с факультета экономики?
12. В отделе работают 7 мужчин и 3 женщины. В командировку отобраны 5 человек. Определить вероятность того, что среди них только одна женщина.
|
|
|
13. Совет директоров состоит из трех бухгалтеров и четырех менеджеров. Планируется создать подкомитет из его членов. Какова вероятность того, что среди трех членов подкомитета два бухгалтера.
14. На складе имеется 15 телевизоров, причем 10 из них изготовлены Симферопольским заводом «Фотон». Найти вероятность, что среди четырех выбранных наудачу телевизоров, два телевизора Симферопольского завода.
15. Устройство содержит 7 элементов, из которых три изношенные. При включении устройства включаются случайным образом три элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.
16. В ящике содержится 10 деталей, из них 4 бракованные. Наудачу извлечены три детали. Найти вероятность того, что среди извлеченных нет бракованных.
17. Из шести карточек с буквами И К С Т У Э наугад одну за другой выбирают четыре карточки и располагают в ряд в порядке появления. Какова вероятность того, что получится слово «КУСТ»?
18. Из 30 вопросов, входящих в билеты зачета, студент подготовил 26. Какова вероятность того, что взятый наудачу студентом билет, содержащий два вопроса, будет состоять из подготовленных им вопросов?
19. В папке 10 квитанций, три из которых заполнены неверно. Наудачу извлечены 6 квитанций. Найти вероятность того, что среди извлеченных нет неверно заполненных квитанций.
20. В компьютерном классе 10 машин, 7 из которых подключены к сети Internet. Наудачу выбраны три машины. Найти вероятность того, что все три подключены к сети Internet.
21. Декан пригласил на беседу двоих студентов, имеющих задолженности по высшей математике, через старосту группы. Староста забыл фамилии приглашенных и отправил двоих из имеющихся пяти задолжников. Какова вероятность того, что это нужные декану студенты?
22. Среди 16 студентов группы, из которых семь девушки, разыгрывается 6 билетов, причем каждый может выиграть только один билет. Какова вероятность того, что среди обладателей билетов окажутся четыре девушки?
23. В отделе работают 6 мужчин и 4 женщины. В командировку отобраны 5 человек. Определить вероятность того, что среди них нет женщин.
24. Совет директоров состоит из трех бухгалтеров и четырех менеджеров. Планируется создать подкомитет из его членов. Какова вероятность того, что среди трех членов подкомитета два менеджера.
25. На складе имеется 15 телевизоров, причем 10 из них изготовлены Симферопольским заводом «Фотон». Найти вероятность, что среди четырех, выбранных наудачу, телевизоров все телевизоры Симферопольского завода.
26. Устройство содержит 7 элементов, из которых три изношенные. При включении устройства включаются случайным образом три элемента. Найти вероятность того, что включенными окажутся все изношенные элементы.
|
|
|
27. В ящике содержится 10 деталей, из них 4 бракованные. Наудачу извлечены три детали. Найти вероятность того, что среди извлеченных нет годных.
28. В чемпионате института по футболу участвуют 6 команд, 4 из которых представляют факультет экономики. Для жеребьевки декан пригласил трех капитанов команд. Какова вероятность того, что двое из них с факультета экономики?
29. Из шести карточек с буквами И К С Т У Э наугад одну за другой выбирают четыре карточки и располагают в ряд в порядке появления. Какова вероятность того, что можно будет прочесть СИЭУ?
30. В папке 10 квитанций, три из которых заполнены неверно. Наудачу извлечены 6 квитанций. Найти вероятность того, что среди извлеченных только одна квитанция заполнена неверно.
Задание 2. Теоремы сложения и умножения вероятностей
1. В мешке смешаны нити, среди которых 80% белые, а остальные – красные. Определить вероятность того, что вынутые наудачу две нити окажутся одного цвета.
2. Рабочий обслуживает три станка. Вероятность того, что в течение смены его внимания потребует первый станок, равна 0,3, второй – 0,35, третий – 0,15. Найти вероятность того, что в течение смены внимания рабочего потребуют какие-либо два станка.
3. Вероятность того, что пришедший в библиотеку студент закажет учебное пособие по теории вероятностей, равна 0,05. Найти вероятность того, что среди троих первых студентов, пришедших в библиотеку, только один закажет учебное пособие по теории вероятностей.
4. Среди производимых рабочим деталей 6% брака. Какова вероятность того, что среди взятых на испытание четырех деталей хотя бы одна бракованная.
5. Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,4, второй – 0,7, третий – 0,3. События, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент услышит вызов радиста.
6. По цели стреляют два торпедных катера. Вероятность попадания в цель для первого катера равна 0,7, для второго – 0,85. Для поражения цели достаточно попадания в нее одной торпеды. Каждый катер делает по одному выстрелу. Определить вероятность того, что цель поражена.
7. Для сообщения об аварии установлены два независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,7, второе – 0,9. Найти вероятность того, что при аварии сработает только одно устройство.
8. Деталь проходит три операции обработки. Вероятность того, что она окажется бракованной после первой операции, равна 0,05, после второй – 0,07, после третьей – 0,1. Найти вероятность того, что после трех операций деталь окажется бракованной, предполагая, что появление брака на отдельных операциях – независимые события.
9. В механизм входят три детали. Работа механизма нарушается, если хотя бы одна деталь выйдет из строя. Вероятность выйти из строя для первой детали – 0,1, для второй – 0,15, для третьей – 0,05. Найти вероятность нормальной работы механизма.
10. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый вопрос, равна 0,9, на второй – 0,6, на третий – 0,8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить, по крайней мере, на один вопрос.
11. Заводом послана автомашина за различными материалами на четыре базы. Вероятность наличия нужного материала на первой базе равна 0,7, на второй – 0,9, на третьей – 0,75, на четвертой – 0,8. Найти вероятность того, что хотя бы на одной базе не окажется нужного материала.
12. Из партии деталей контролер отбирает стандартные. Вероятность того, что наудачу взятая деталь стандартная, равна 0,85. Найти вероятность того, что из трех проверенных деталей только две будут стандартные.
13. В первом ящике 1 белый, 3 красных и 1 синий шар, во втором 3 белых, 2 красных и 5 синих шаров. Из каждого ящика вынули по шару. Какова вероятность того, что среди вынутых шаров хотя бы один красный шар?
14. Вероятности того, что нужная сборщику деталь содержится в первом, втором, третьем ящике, соответственно равны 0,7; 0,5; 0,9. Найти вероятность того, что деталь содержится хотя бы в одном ящике.
15. Студент записан в три библиотеки, в которых он разыскивает нужную ему книгу по комбинаторике. Вероятность найти книгу в первой библиотеке равна 0,2, во второй – 0,7, в третьей – 0,5. Найти вероятность того, что книгу можно найти хотя бы в одной библиотеке.
16. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него будут сброшены три бомбы с вероятностями попадания соответственно равными 0,7; 0,2; 0,85.
17. В одном ящике 3 белых и 7 красных шаров, в другом 6 белых и 4 красных. Из каждого ящика наудачу извлекают по одному шару. Найти вероятность того, что хотя бы из одного ящика будет извлечен белый шар.
18. Вероятность того, что в течение одной смены станок выйдет из строя, равна 0,1. Какова вероятность того, что не произойдет ни одной неполадки за три смены?
19. В первом ящике 1 белый, 3 красных и 1 синий шар, во втором 3 белых, 2 красных и 5 синих шаров. Из каждого ящика вынули по шару. Какова вероятность того, что среди вынутых шаров нет синих?
20. В мешке смешаны нити, среди которых 80% белые, а остальные – красные. Определить вероятность того, что вынутые наудачу две нити окажутся разных цветов.
21. Рабочий обслуживает три станка. Вероятность того, что в течение смены его внимания потребует первый станок, равна 0,3, второй – 0,35, третий – 0,15. Найти вероятность того, что в течение смены внимания рабочего потребует хотя бы один станок.
22. Для сообщения об аварии установлены два независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,7, второе – 0,9. Найти вероятность того, что при аварии сработает хотя бы одно устройство.
23. В механизм входят три детали. Работа механизма нарушается, если хотя бы одна деталь выйдет из строя. Вероятность выйти из строя для первой детали – 0,1, для второй – 0,15, для третьей – 0,05. Найти вероятность того, что работа механизма будет нарушена.
24. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый вопрос, равна 0,9, на второй – 0,6, на третий – 0,8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить, по крайней мере, на два вопроса.
25. Заводом послана автомашина за различными материалами на четыре базы. Вероятность наличия нужного материала на первой базе равна 0,7, на второй – 0,9, на третьей – 0,75, на четвертой – 0,8. Найти вероятность того, что только на одной базе не окажется нужного материала.
26. Из партии деталей контролер отбирает стандартные. Вероятность того, что наудачу взятая деталь стандартная, равна 0,85. Найти вероятность того, что из трех проверенных деталей хотя бы одна нестандартная.
27. Вероятности того, что нужная сборщику деталь содержится в первом, втором, третьем ящике, соответственно равны 0,7; 0,5; 0,9. Найти вероятность того, что деталь содержится, по крайней мере, в двух ящиках.
28. Студент записан в три библиотеки, в которых он разыскивает нужную ему книгу по комбинаторике. Вероятность найти книгу в первой библиотеке равна 0,2, во второй – 0,7, в третьей – 0,5. Определить вероятность того, что книгу можно найти, по крайней мере, в двух библиотеках.
29. В одном ящике 3 белых и 7 красных шаров, в другом 6 белых и 4 красных. Из каждого ящика наудачу извлекают по одному шару. Найти вероятность того, что оба извлеченных шара красные.
30. В первом ящике 1 белый, 3 красных и 1 синий шар, во втором 3 белых, 2 красных и 5 синих шаров. Из каждого ящика вынули по шару. Какова вероятность того, что среди вынутых шаров нет белых шаров?
Задание 3. Формула полной вероятности. Формулы Бейеса
1. Имеется два одинаковых ящика с шарами. В первом ящике 4 белых и 6 красных шаров, во втором 5 белых и 10 красных. Наудачу выбирают один ящик и извлекают из него шар. Какова вероятность того, что извлеченный шар окажется белым?
2. Предприятие имеет три источника поставки комплектующих – фирмы А, В, С. На долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Из практики известно, что 10% поставляемых фирмой А деталей – бракованные, В – 5% и С – 6%. Какова вероятность того, что наугад взятая деталь стандартная?
3. В студенческой группе 20 человек. Из них 4 человека сдали экзамен по высшей математике на «отлично», 11 на «хорошо» и 5 на «удовлетворительно». Вероятность решить предложенную задачу для отличника составляет 0,9, для хорошиста 0,8, для троечника 0,7. Определить вероятность того, что наудачу выбранный студент не решит задачу.
4. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника 0,9, для велосипедиста 0,8 и для бегуна 0,75. Найти вероятность того, что наудачу выбранный спортсмен не выполнит норму.
5. В первой урне 3 белых и 7 черных шаров, во второй – 6 белых и 4 черных шаров. Из второй урны в первую переложили один шар, а затем из первой урны вынули наугад один шар. Какова вероятность того, что вынутый шар ранее находился во второй урне, если известно, что он белый.
6. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы второго курса 4 студента, из второй группы 6 студентов, из третьей группы 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадет в сборную института, соответственно равны 0,6, 0,9, 0,5. Найти вероятность того, что наудачу выбранный студент не попадет в сборную.
7. В первом ящике 20 деталей, из них 15 стандартные. Во втором ящике 25 деталей, из них 20 стандартные. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика – стандартная.
8. Сборщик получил 5 коробок деталей, изготовленных заводом №1, и 4 коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна, равна 0,9, а завода №2 – 0,72. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь.
9. В студенческой группе 25 человек. Из них 5 человек сдали экзамен по высшей математике на «отлично», 12 на «хорошо» и 8 на «удовлетворительно». Вероятность решить предложенную задачу для отличника составляет 0,9, для хорошиста 0,8, для троечника 0,7. Определить вероятность того, что наудачу выбранный студент решит задачу.
10. На заводе изготовляют комплектующие детали. Первая машина производит 25% всех изделий, вторая 35%, третья 40%. Брак составляет соответственно 5%, 4% и 10%. Какова вероятность того, что случайно выбранная деталь имеет дефект?
11. В группе спортсменов 15 лыжников, 9 велосипедистов и 6 бегунов. Вероятность выполнить квалификационную норму такова: для лыжника 0,95, для велосипедиста 0,9 и для бегуна 0,7. Найти вероятность того, что наудачу выбранный спортсмен выполнит норму.
12. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы второго курса 5 студентов, из второй группы 4 студента, из третьей группы 6 студентов. Вероятности того, что студент первой, второй и третьей группы попадет в сборную института, соответственно равны 0,6, 0,9, 0,7. Найти вероятность того, что наудачу выбранный студент попадет в сборную.
13. Предприятие имеет три источника поставки комплектующих – фирмы А, В, С. На долю фирмы А приходится 45% общего объема поставок, В – 25% и С – 30%. Из практики известно, что 10% поставляемых фирмой А деталей – бракованные, В – 8% и С – 7%. Какова вероятность того, что взятая наугад и оказавшаяся бракованной деталь получена от фирмы А?
14. В первом ящике 30 деталей, из них 20 стандартные. Во втором ящике 20 деталей, из них 15 стандартные. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика – бракованная.
15. Имеется два одинаковых ящика с шарами. В первом ящике 10 белых и 5 черных шаров, во втором 3 белых и 7 черных. Наудачу выбирают один ящик и извлекают из него шар. Какова вероятность того, что извлеченный шар окажется белым?
16. Сборщик получил 4 коробки деталей, изготовленных заводом №1, и 6 коробок деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна, равна 0,7, а завода №2 – 0,8. Сборщик наудачу извлек деталь из наудачу взятой коробки. Извлечена стандартная деталь. Определить вероятность того, что она изготовлена заводом №2.
17. На заводе изготовляют комплектующие детали. Первая машина производит 30% всех изделий, вторая 50%, третья 20%. Брак составляет соответственно 7%, 6% и 10%. Какова вероятность того, что случайно выбранная деталь стандартная?
18. Предприятие имеет три источника поставки комплектующих – фирмы А, В, С. На долю фирмы А приходится 40% общего объема поставок, В – 25% и С – 35%. Из практики известно, что 10% поставляемых фирмой А деталей – бракованные, В – 4% и С – 6%. Какова вероятность того, что наугад взятая деталь бракованная?
19. В первой урне 5 белых и 15 черных шаров, во второй – 13 белых и 7 черных шаров. Из второй урны в первую переложили один шар, а затем из первой урны вынули наугад один шар. Определить вероятность того, что вынутый шар – белый.
20. В студенческой группе 20 человек. Из них 4 человека сдали экзамен по высшей математике на «отлично», 11 на «хорошо» и 5 на «удовлетворительно». Вероятность решить предложенную задачу для отличника составляет 0,9, для хорошиста 0,8, для троечника 0,7. Наудачу выбранный студент решил задачу. Определить вероятность того, что это отличник.
21. Имеется два одинаковых ящика с шарами. В первом ящике 14 белых и 6 красных шаров, во втором 15 белых и 10 красных. Наудачу выбирают один ящик и извлекают из него шар. Какова вероятность того, что извлеченный шар окажется красным?
22. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника 0,9, для велосипедиста 0,8 и для бегуна 0,75. Наудачу выбранный спортсмен выполнил норму. Определить вероятность того, что это велосипедист.
23. На заводе изготовляют комплектующие детали. Первая машина производит 25% всех изделий, вторая 35%, третья 40%. Брак составляет соответственно 6%, 4% и 9%. Случайно выбранная деталь оказалась бракованной. Какова вероятность того, что она была произведена первой машиной?
24. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы второго курса 4 студента, из второй группы 6 студентов, из третьей группы 5 студентов. Вероятность того, что студент первой, второй и третьей группы попадет в сборную института, соответственно равна 0,6, 0,8, 0,5. Наудачу выбранный студент попал в сборную. Определить вероятность того, что это студент из первой группы.
25. Сборщик получил 6 коробок деталей, изготовленных заводом №1, и 4 коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна, равна 0,8, а завода №2 – 0,75. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена бракованная деталь.
26. На заводе изготовляют комплектующие детали. Первая машина производит 40% всех изделий, вторая 35%, третья 25%. Брак составляет соответственно 5%, 4% и 9%. Случайно выбранная деталь оказалась стандартной. Какова вероятность того, что она была произведена третьей машиной?
27. Имеется два одинаковых ящика с шарами. В первом ящике 10 белых и 15 черных шаров, во втором 13 белых и 17 черных. Наудачу выбирают один ящик и извлекают из него шар. Какова вероятность того, что извлеченный шар окажется черным?
28. Предприятие имеет три источника поставки комплектующих – фирмы А, В, С. На долю фирмы А приходится 35% общего объема поставок, В – 25% и С – 40%. Из практики известно, что 10% поставляемых фирмой А деталей – бракованные, В – 5% и С – 7%. Какова вероятность того, что взятая наугад и оказавшаяся стандартной деталь получена от фирмы В?
29. В первой урне 15 белых и 5 черных шаров, во второй – 14 белых и 6 черных шаров. Из второй урны в первую переложили один шар, а затем из первой урны вынули наугад один шар. Определить вероятность того, что вынутый шар – черный.
30. Сборщик получил 14 коробок деталей, изготовленных заводом №1, и 16 коробок деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна, равна 0,75, а завода №2 – 0,8. Сборщик наудачу извлек деталь из наудачу взятой коробки. Извлечена нестандартная деталь. Определить вероятность того, что она изготовлена заводом №1.
Задание 4. Повторные независимые испытания по схеме Бернулли
1. Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди 600 взятых наугад изделий 25 бракованных.
2. Вероятность получения хорошего результата при проведении маркетинговых исследований равна 0,7. Найти вероятность наивероятнейшего числа удачных исследований, если общее их количество равно 8.
3. Среди семян ржи имеется 0,2% семян сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить не более 3 семян сорняков?
4. Вероятность появления успеха в каждом испытании равна 0,4. Найти вероятность того, что при 550 испытаниях успех наступит не менее 210 и не более 240 раз.
5. Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная станция обслуживает 900 абонентов. Какова вероятность того, что в течение часа позвонят пять абонентов?
6. В первые классы должно быть принято 400 детей. Определить вероятность того, что среди них окажется 200 девочек, если вероятность рождения мальчика равна 0,515.
7. Вероятность рождения мальчика равна 0,515, а девочки – 0,485. В некоторой семье шестеро детей. Найти вероятность того, что среди них не больше двух девочек.
8. Имеется группа, состоящая из 500 человек. Найти вероятность того, что у двух человек день рождения придется на Новый год. Считать, что вероятность рождения в фиксированный день равна 1/365.
9. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 300 выстрелах мишень будет поражена не менее 230 раз.
10. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Какова вероятность того, что из четырех вынутых шаров окажется два черных?
11. Известно, что 5% продукции, поставляемой заводом на торговую базу, не удовлетворяет всем требованиям стандарта. На базу поступило 9 изделий. Найти наивероятн
|
|
|
