 |
Биномиальное распределение.
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться с одной и той же вероятностью р и не появиться с вероятностью 
. Рассмотрим в качестве дискретной случайной величины Х – число появлений события А в этих испытаниях и найдем закон ее распределения. Возможные значения Х таковы: 
. Соответствующие вероятности находим по формуле Бернулли:
,
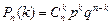где k = 0; 1; 2; …; n.
Записанная формула выражает биноминальный закон распределения.
В виде таблицы этот закон можно записать так:
| x | … | n | |||
| р |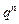 
| 
| 
| … | 
|
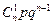
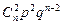
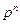
Для биномиального закона 
; 
.
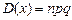Пример. Вероятность попадания стрелком в мишень равна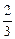 
. Стрелок сделал 15 выстрелов. Случайная величина Х – число попаданий в мишень. Найти математическое ожидание и дисперсию случайной величины Х.
Решение. Так как имеем биномиальное распределение, для которого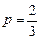 
, 
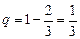и 
, то
;
.
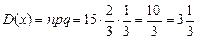Распределение Пуассона
Пусть производится n независимых испытаний (n велико), в каждом из которых событие А может появиться с одной и той же вероятностью р (р мало). Случайная величина Х может принимать любые целые неотрицательные значения (0; 1; 2; …; n), а соответствующие им вероятности можно находить по формуле:
,
где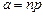 
, 
.
Формула выражает закон распределения Пуассона вероятностей массовых редких событий. Для этого закона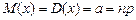 
.
Нормальное распределение
При решении задач, которые выдвигает практика, часто встречается закон нормального распределения непрерывных случайных величин.
Нормальный закон распределения характеризуется плотностью распределения
.
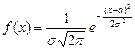В этом законе два параметра: а и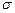 
; а – это математическое ожидание, 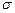– среднее квадратическое отклонение, т.е. 
; 
.
 |
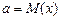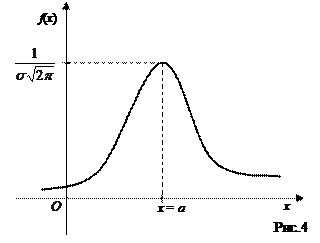График плотности распределения называют нормальной кривой (кривой Гаусса). Она расположена над осью х. Эта кривая симметрична относительно прямой х = а; ее максимальная ордината
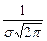(рис.4).
Ось х является асимптотой графика.
Изменение величины параметра а не изменяет формулы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси х.
 |
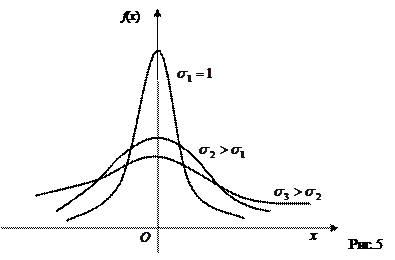Если же изменяется параметр
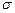, то изменяется и вид кривой. С возрастанием 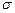кривая становится более пологой, т.е. сжимается к оси х; при убывании 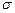нормальная кривая становится более островершинной (рис.5).
Но при любых значениях параметров а и 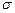площадь, ограниченная нормальной кривой и осью х, остается равной 1. При а = 0 и 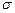= 1 нормальную кривую называют нормированной и плотность распределения 
.
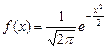Если случайная величина Х распределена по нормальному закону, то вероятность того, что Х примет значение из интервала 
находят по формуле:
.
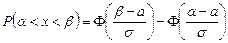Пример.Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10; 50).
Решение. По условию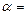 
10;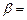 
50; а = 30; 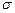= 10. Найдем искомую вероятность
,
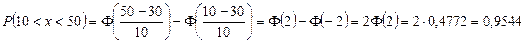значение 
=0,4772 (из приложения 2).
При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. Если для изученного распределения это различие имеет небольшое значение, то можно предположить, что это распределение близко к нормальному. С этой целью вводят специальные характеристики – асимметрию и эксцесс.
Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:
.
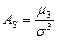Эксцессом теоретического распределения называют характеристику, которая определяется равенством:
.
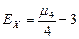Примечание. Для нормального распределения эти характеристики равны нулю.
