 |
Числовые характеристики случайных величин
|
|
|
|
При решении ряда практических задач нет необходимости знать все возможные значения случайной величины и их вероятности, а удобнее пользоваться некоторыми количественными показателями, которые называют числовыми характеристиками случайной величины. Основными из них являются математическое ожидание, дисперсия, среднее квадратное отклонение, моменты различных порядков, мода, медиана.
Математическим ожиданием дискретной случайной величины 
называют сумму произведений всех ее возможных значений на их вероятности:
Математическое ожидание служит характеристикой среднего значения случайной величины.
Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
.
Вычислять дисперсию удобно по формуле:
,
где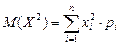 
.
Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
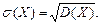
Дисперсия и среднее квадратическое отклонение служат характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания.
Пример. Найти математическое ожидание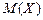 
, дисперсию 
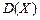и среднее квадратическое отклонение 
дискретной случайной величины , закон распределения которой задан в виде таблицы:
| 
| 
| 
| 
| 
|
| 
| 
| 
|
|
|
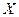
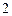
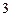
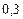
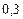
Решение. Математическое ожидание равно сумме произведений всех возможных значений на их вероятности:
.
Для вычисления дисперсии воспользуемся формулой:
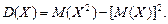
Составим закон распределения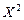 
:
|
|
|
| 
| 
| 
|
|
|
|
|
|
|
|
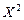
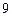
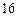
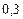
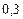
Найдем математическое ожидание :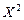
.
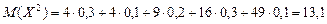Подставив в формулу для вычисления дисперсии 
и 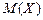найденное ранее, получим:
.
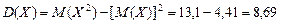Найдем искомое среднее квадратическое отклонение:
|
|
|
.
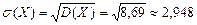Начальным моментом порядка k случайной величины называют математическое ожидание величины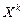 
:
,
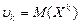где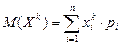 
.
В частности, 
, 
.
Центральным моментом порядка k случайной величины называют математическое ожидание величины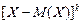 
:
.
В частности, 
, 
.
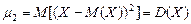Центральные моменты целесообразно вычислять, используя формулы, выражающие центральные моменты через начальные:
Пример. Дискретная случайная величина задана законом распределения:
|
| 
|
|
|
| 
|
|
|
|
|
|
|
|
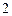
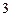
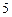
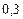
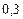
Найти начальные и центральные моменты первого, второго и третьего порядков.
Решение. Найдем начальный момент первого порядка:
.
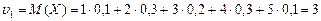Составим закон распределения величины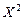 
:
|
|
| ||||
|
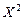
| 0,1 | 0,3 | 0,2 | 0,3 | 0,1 |
Найдем начальный момент второго порядка:
.
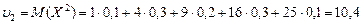Составим закон распределения величины 
:
|
| |||||
|
| 0,1 | 0,3 | 0,2 | 0,3 | 0,1 |
Найдем начальный момент третьего порядка:
.
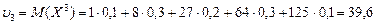Центральный момент первого порядка всегда равен нулю: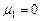 
.
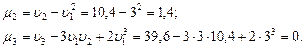
Математическое ожидание непрерывной случайной величины , возможные значения которой принадлежат всей оси 
, определяется равенством
,
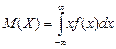где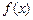 
–дифференциальная функция.
В частности, если все возможные значения принадлежат интервалу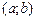 
, то
.
Дисперсия непрерывной случайной величины , возможные значения которой принадлежат всей оси , определяется равенством
,
или равносильным равенством
.
В частности, если все возможные значения принадлежат интервалу 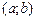, то
,
или 
.
Среднее квадратическое отклонение непрерывной случайной величины определяется так же, как и для дискретной величины:
.
Пример. Случайная величина задана дифференциальной функцией
Найти математическое ожидание 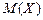и среднее квадратическое отклонение .
Решение. Найдем математическое ожидание
.
Для вычисления дисперсии воспользуемся формулой
.
Учитывая, что 
, получим
.
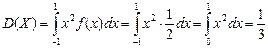Найдем искомое среднее квадратическое отклонение
.
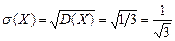ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
|
|
|
Рассмотрим некоторые законы распределения случайных величин.
|
|
|
