 |
Геометрическая вероятность
|
|
|
|
Геометрическое определение вероятности появилось благодаря попытке отказаться от конечности m и n.
Пусть на плоскости имеется некоторая область G и в ней содержится другая область g. Требуется найти вероятность того, что точка, взятая наудачу в области G, попадет в область g.
При этом выражению «точка, взятая наудачу в области G», придается следующий смысл: эта точка может попасть в любую точку области G.
Вероятность попадания точки в какую-либо область G пропорциональна мере (mes) этой части (длине, площади, объему и т.д.) и не зависит от ее расположения и формы:
;
(геометрическое определение вероятности).
Пример. Круглый диск радиуса R разбит на два сектора. Длина дуги одного из них (заштрихованного) равна радиусу R. По быстро вращающемуся диску произведен выстрел. Найти вероятность попадания в этот сектор.
Решение.
Событие А – попадание в сектор.
В данном случае, в качестве меры выступает площадь;
, где 
– площадь круга; 
– площадь сектора.
;
площадь кругового сектора, соответствующего центральному углу в 
радиан: 
;
длина дуги, соответствующей центральному углу в радиан: 
;
По условию: 
рад.
, откуда
.
Пример. (задача о встрече). Два студента А и В условились встретиться в определенном месте во время перерыва, между 13 ч. и 13 ч. 50 мин. Пришедший первым ждет другого в течение 10 мин., после чего уходит. Чему равна вероятность их встречи, если приход каждого из них в течение указанных 50 мин. может произойти наудачу и моменты прихода неизвестны.
Решение. Обозначим момент прихода студента А через x, а студента В через y.
Для того чтобы они встретились, необходимо и достаточно, чтобы 
.
Изобразим x и y как декартовы координаты на плоскости, а в качестве масштаба выберем 1 минуту.
|
|
|
Всевозможные исходы изобразятся точками квадрата со стороной 50:
;
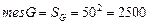Исходы, благоприятствующие встрече, – точками заштрихованной области.
;
Откуда
.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Формулы комбинаторики составляют теоретическую базу при использовании классического определения вероятности, которое в прикладных задачах играет большую роль.
В зависимости от правил составления можно выделить три типа комбинаций:
q Перестановки;
q Размещения;
q Сочетания;
I. Перестановки
Комбинации из n элементов, которые отличаются друг от друга только порядком элементов, называют перестановками.
Обозначаются символом 
;
;
, (
– эн факториал), при этом 
.
Из можно выделить 
, если 
.
Например, 
Пример. В соревновании участвовало 4 команды, сколько существует вариантов распределить места между ними.
Решение. Количество вариантов распределения четырех команд по местам – равно числу перестановок из четырех элементов: 
.
Пример. В ящике пять одинаковых пронумерованных кубиков. Наудачу по одному извлекают все кубики из ящика. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.
Решение. Обозначим 
событие, состоящее в том, что номера извлеченных кубиков появятся в возрастающем порядке.
Благоприятствует событию только один исход, 
(из всех возможных комбинаций номеров только одна с порядком возрастания номеров).
Общее число возможных исходов – количество комбинаций из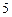 
номеров, 
.
Искомая вероятность: 
.
II. Размещения
Комбинации из n элементовпо k элементов, которые отличаются друг от друга или самими элементами, илипорядком элементов, называют размещениями.
Обозначаются символом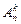 
– количество всех имеющихся элементов;
– количество элементов в каждой комбинации, 
;
.
Пример. Сколько существует вариантов размещения 
призовых мест, если в розыгрыше участвуют 7 команд?
|
|
|
Решение. Необходимо просчитать число возможных комбинаций, извлеченных из 7 элементов и включающих по 3 элемента (причем {I–«Таврия», II–«Динамо», III–«Спартак»} и {I–«Динамо», II–«Таврия», III–«Спартак»} – различные комбинации). Используем число размещений из 7 элементов по 3:
.
Пример. Из пяти карточек с буквами О, П, Р, С, Т наугад одну за другой выбирают три и располагают в ряд в порядке появления. Какова вероятность того, что получится слово «ТОР»?
Решение. Обозначим событие, состоящее в том, что получится слово «ТОР».
Благоприятствует событию только один исход, (комбинация букв «ТОР»).
Общее число возможных исходов – равно числу способов, которыми можно отобрать 3 карточки из имеющихся 5, получая при этом комбинации букв, отличающиеся либо самими буквами (СОР – ТОР), либо их порядком (РОТ – ОРТ). Оно определяется числом размещений из 5 элементов по 3:
.
Искомая вероятность:
.
III. Сочетания
Сочетаниями называют все возможные комбинации из n элементовпо k элементов, которые отличаются друг от друга, по крайней мере, хотя бы одним элементом.
Обозначаются символом 
– количество всех имеющихся элементов;
– количество элементов в каждой комбинации, ;
.
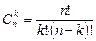Свойства сочетаний
1) 
;
2) 
;
3) 
.
Пример. Сколькими способами можно выбрать 3 студентов из группы численностью 30 человек.
Решение. Необходимо просчитать число возможных комбинаций, извлеченных из 30 элементов и включающих по 3 элемента (причем комбинации: {Пархоменко, Мурейко, Божок} и {Мурейко, Божок, Пархоменко} – одинаковые комбинации). Используем число размещений из 30 элементов по 3:
.
Пример. В урне 5 белых и 4 красных шара. Из урны наудачу извлекают 3 шара. Найти вероятность того, что извлеченные шары – белые.
Решение. Обозначим событие, состоящее в том, что все 3 шара будут белыми.
Всего в урне 
шаров.
Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 3 шара из 9:
.
Число исходов, благоприятствующих событию , равно числу способов, которыми можно отобрать 3 белых шара из имеющихся 5 белых:
.
Искомая вероятность равна:
.
Пример. В ящике имеется 11 одинаковых шаров. Причем 4 из них окрашены в синий цвет, а остальные белые. Наудачу извлекают 5 шаров. Найти вероятность того, что среди них 2 синих.
|
|
|
Решение. Обозначим событие, состоящее в том, что среди извлеченных 5 шаров 2 синих.
Обще число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 5 шаров из 11, т.е.
.
Подсчитаем число исходов, благоприятствующих событию : 2 синих шара можно взять из 4 имеющихся синих шаров 
способами; при этом остальные 
шара должны быть белыми, взять же 3 белых шара из имеющихся 7 можно 
способами. Следовательно, число благоприятствующих исходов равно:
.
Искомая вероятность:
.
Рассмотрим типовую задачу: В партии из 
деталей имеется стандартных. Наудачу отобраны 
деталей. Вероятность того, что среди отобранных деталей ровно будет стандартных можно находить по формуле:
.
|
|
|
