 |
Неопределенный интеграл, его свойства.
|
|
|
|
Построение графиков функции с помощью производной.
Алгоритм исследования функции 
:
1.Находим область определения функции .
2. Если 
, то функция четная.
График четной функции симметричен относительно оси OY.
Если 
, то функция нечетная.
График нечетной функции симметричен относительно начала координат.
3.Находим точки пересечения графика с осями координат.
Находим нули функции - это точки пересечения графика функции с осью абсцисс (OX).
Для этого мы решаем уравнение 
.
Находим точку пересечения графика функции с осью ординат (OY).
Для этого ищем значение функции при 
.
4.Находим асимптоты графика функции.
5. Исследуем функцию с помощью производной: находим промежутки возрастания и убывания функции, а также точки максимума и минимума.
Для этого мы следуем привычному алгоритму.
а) Находим производную 
б) Приравниваем производную к нулю и находим корни уравнения 
- это стационарные точки.
в) Находим промежутки знакопостоянства производной. Промежутки, на которых производная положительна, являются промежутками возрастания функции.
Промежутки, на которых производная отрицательна, являются промежутками убывания функции.
Точки, в которых производная меняет знак с плюса на минус, являются точками максимума.
Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума.
6.Находим точки перегиба и промежутки выпуклости и вогнутости.
Пример 1. Исследуйте функцию 
и постройте ее график.
Решение.
1.Найдем область определения функции.
При 
знаменатель дроби равен нулю,
следовательно, прямые 
и 
являются вертикальными асимптотами графика функции .
2.Исследуем функцию на четность.
|
|
|
Получили, что ,
следовательно, функция - нечетная, и график функции симметричен относительно начала координат.
3. Найдем точки пересечения с осями координат.
а) Точки пересечения с осью ОХ (y=0)
б) Точка пересечения с осью ОY (x=0)
График нашей функции проходит через начало координат.
4.Найдем асимптоты графика функции .
Вертикальные асимптоты мы уже нашли в п.1, это прямые и .
Уравнение горизонтальной асимптоты функции имеет вид 
, где
.
Степень числителя дроби 
на единицу больше степени знаменателя, поэтому 
не существует, и график функции не имеет горизонтальной асимптоты.
Попробуем найти наклонную асимптоту.
Уравнение наклонной асимптоты имеет вид 
.
Коэффициенты 
и 
вычисляются следующим образом:
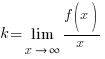
В нашем случае
.
(Степень знаменателя на единицу больше степени числителя).
То есть уравнение наклонной асимптоты имеет вид 
.
5.Найдем промежутки возрастания и убывания функции и экстремумы.
а) Найдем производную функции
б) Приравняем производную к нулю: 
; 
; 
в) Нанесем нули производной и корни ее знаменателя на числовую ось, расставим знаки и найдем точки экстремума и промежутки возрастания и убывания.
Найдем значение функции в точках экстремума:
Неопределенный интеграл, его свойства.
Определение. Совокупность F(x)+C всех первообразных функции f(x) на множестве Х называется неопределенным интегралом и обозначается:
- (1)
В формуле (1) f(x)dx называется подынтегральным выражением, f(x) – подынтегральной функцией, х – переменной интегрирования, а С – постоянной интегрирования.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Рассмотрим свойства неопределенного интеграла, вытекающие из его определения.
1. Постоянный множитель а (а≠0) можно выносить за знак неопределенного интеграла:
2. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от этих функций:
|
|
|
3. Если F(x) – первообразная функции f(x), то:
Таблица основных неопределенных интегралов
1.  (n≠-1).
2.  (a >0, a≠1).
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
| 12. 
13. 
14.  (a≠0).
15.  (a≠0).
16. 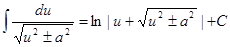 (|u| > |a|).
17.  (|u| < |a|).
18. 
19. 
|
|
|
|
