Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами.

Определение.Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида

y^//+py^/+qy=h(x),

где p и q – числа, h(x) – некоторая функция от x.

Если в этом уравнении 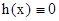, то оно называется однородным линейным дифференциальным уравнением второго порядка.

Рассмотрим решение однородного уравнения:

.

Этому явлению может быть поставлено в соответствие квадратное уравнение вида: , называемое характеристическим.

Его корни, как известно, определяются формулами:

Возможны следующие три случая:

1) корни уравнения – действительные и различные;

2) корни – действительные и равные;

3) корни уравнения – комплексно-сопряженные.

 

Случай 1. Дискриминант характеристического уравнения положителен, т.е. p²-4q>0. Тогда оба корня действительные и различные. В этом случае общее решение однородного уравнения имеет вид:

где c₁, c₂ – произвольные постоянные.

Частное решение: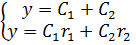

Случай 2. Дискриминант характеристического квадратного уравнения равен нулю, т.е. p²-4q=0.

Тогда оба корня  действительные и равные. В этом случае общее решение однородного уравнения имеет вид:

Частное решение:

Случай 3. Дискриминант характеристического квадратного уравнения отрицателен, т.е. p²-4q<0.

Тогда говорят, что квадратное уравнение не имеет действительных корней (или что оба корня являются комплексно-сопряженными). В этом случае, обозначая , общее решение однородного уравнения дается в виде:   .

Частное решение:

Числовые ряды.

Пусть задана бесконечная последовательность чисел: u ₁, u ₂, …, u_n, …

Приведем пример числовой последовательности: .
Построим из этой последовательности выражение: u ₁ + u ₂ + u ₃ +…+ u_n +…

Это выражение называется числовым рядом, где слагаемые u ₁, u ₂, u ₃,… называются членами ряда, а член u_n  - его общим членом. Таким образом, можно сказать, что числовой ряд – это бесконечная сумма чисел.

Числовой ряд часто записывается в виде .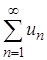

Здесь:
– математический значок суммы;
– общий член ряда
– переменная-«счётчик». Запись обозначает, что проводится суммирование от 1 до «плюс бесконечности», то есть, сначала у нас , затем , потом , и так далее – до бесконечности. Вместо переменной иногда используется переменная 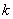или .

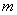Замечание 1. Перечисление членов ряда не всегда может начинаться при n =1. Часто первым является член ряда с номером n =0 или, например, n =2. В таком случае и записывают ряд в виде  или

Замечание 2. В формулах общего члена различных числовых рядов достаточно часто встречается знак факториала:

n!=1 × 2 × 3 × 4 × … × (n -1) × n.

В частности, 1!=1, 2!=2, 3!=6 и т.д.; (n +1)!= n! × (n +1). Считается, что 0!=1.

  Таким образом. Числовым рядом называется сумма вида

, (1.1), где , , 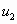,…, ,…, называемые членами ряда, образуют бесконечную последовательность; член называется общим членом ряда.

Если члены ряда:

· числа, то ряд называется числовым;

· числа одного знака, то ряд называется знакопостоянным;

· числа разных знаков, то ряд называется знакопеременным;

· положительные числа, то ряд называется знакоположительным;

· числа, знаки которых строго чередуются, то ряд называется знакочередующимся;

· функции, то ряд называется функциональным;

· степени , то ряд называется степенным;

· тригонометрические функции, то ряд называется тригонометрическим.

 

Суммы

…………..

,

составленные из первых членов ряда (1.1), называются частичными суммами этого ряда.

Или Сумма конечного числа n первых членов ряда называется n -ой частичной суммой ряда:

S_n = u ₁ + u ₂ + … + u_n

Пример 1

Выражение: является рядом. Составьте частичные суммы.

                       Пример 2 Написать первые четыре члена ряда с общим членом

Решение. Полагая в формуле для общего члена n=1,2,3,4, получаем:

; ; ;

Итак,

 

Пример 3. Написать первые четыре члена ряда, общий член которого задан формулой .

Решение. Полагая в данной формуле n = 1,2,3,4,5,6, получаем

; ;

; ;

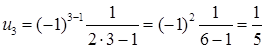Таким образом, данный ряд можно записать так:

Пример 4. Записать первые три члена ряда:
Сначала , тогда: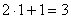
Затем , тогда:
Потом , тогда:

Пример 5. Записать первые три члена ряда:

На самом деле задание выполняется устно: мысленно подставляем в общий член ряда сначала , потом и . В итоге:

 

Пример 6. Записать сумму в свёрнутом виде с общим членом ряда

Здесь нет какого-то четкого алгоритма решения, закономерность нужно просто увидеть.
В данном случае:

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: