 |
Предельный признак сравнения.
|
|
|
|
Рассмотрим два положительных числовых ряда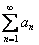 
и 
. Если предел отношения общих членов этого ряда равен конечному, отличному от нуля числу 
: 
, то оба ряда сходятся или расходятся одновременно.
Пример 4. Исследовать ряд на сходимость 
Решение. Сравним данный ряд со сходящимся рядом 
. Используем предельный признак сравнения. Известно, что ряд – сходится. Если нам удастся показать, что 
равен конечному, отличному от нуля числу, то будет доказано, что ряд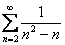 
– тоже сходится.
Получено конечное, отличное от нуля число, значит, исследуемый ряд сходится вместе с рядом .
Пример 5. Исследовать ряд на сходимость 
Решение. Мы видим, что и в числителе и в знаменателе у нас многочлены, причем, в знаменателе многочлен находится под корнем. Подбираем ряд для сравнения 
.
1) Сначала нужно найти старшую степень знаменателя. Если бы не было корня, то, понятно, что старшая степень знаменателя равнялась бы четырем. Что делать, когда есть корень? Мысленно или на черновике отбрасываем все члены, кроме старшего: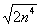 
. Если есть константа, её тоже отбрасываем: 
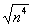. Теперь извлекаем корень: 
. Таким образом, старшая степень знаменателя равна двум.
2) Выясняем старшую степень числителя. Очевидно, что она равна единице.
3) Из старшей степени знаменателя вычитаем старшую степень числителя: 2 – 1 = 1
Таким образом, наш ряд нужно сравнить с рядом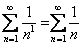 
, то есть, с расходящимся гармоническим рядом.
Само оформление решения должно выглядеть примерно так:
Сравним данный ряд с расходящимся гармоническим рядом 
. Используем предельный признак сравнения:
Получено конечное, отличное от нуля число, значит, исследуемый ряд расходится вместе с гармоническим рядом .
Признак Даламбера
|
|
|
Рассмотрим числовой ряд с положительными членами 
.
Если 
, то:
ряд сходится, если l<1; ряд расходится, если l>1; в случае l=1 вопрос о сходимости или расходимости ряда остается открытым.
Пример 6. Доказать сходимость ряда 
Решение. Общий член ряда определяется формулой 
. Заменяя в этой формуле n на n + 1, получаем последующий член 
.
Составим отношение последующего члена к предыдущему:
: 
.
Найдем предел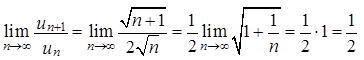 
Так как l =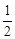 
<1, то ряд сходится (по признаку Даламбера).
Пример 7. Исследовать на сходимость ряд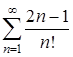 
.
Решение. Здесь 
, 
,
Согласно признаку Даламбера, ряд сходится.
Пример 8. Исследовать сходимость ряда 
.
Решение. Здесь 
поэтому 
>1, значит, ряд расходится.
Замечание.
Напомним, что при вычислении пределов такого вида используют следующие свойства функции ln:
для любой функции у справедливо тождество 
;
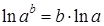для любых а>0, b;
ln y ~ y -1 при y ® 1.
Пример 9. Определить сходимости рядов:
Сходится.
Пример 10. Исследовать сходимость числового ряда. 
Решение:
В этом задани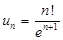и 
и 
Применим признак Даламбера. Найдем 
, так 
то ряд расходится
Признак Коши.
Пусть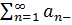 
ряд с неотрицательными членами. Если 
сходится при 
.
Для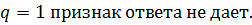 
Степенные ряды.
Степенным рядом называется ряд вида
,
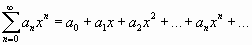где числа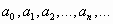 
называются коэффициентами ряда, а член 
- общим членом ряда.
Областью сходимости степенного ряда называется множество всех значений 
, при которых данный ряд сходится.
Число 
называется радиусом сходимости степенного ряда, если при 
ряд сходится и притом абсолютно, а при 
ряд расходится.
Радиус сходимости найдем, используя признак Даламбера:
( не зависит от 
),
,
т.е. если степенной ряд сходится при любых , удовлетворяющих данному условию и расходится при 
.
Отсюда следует, что если существует предел
,
то радиус сходимости ряда 
равен этому пределу и степенной ряд сходится при , т.е. в промежутке 
, который называется промежутком (интервалом) сходимости.
|
|
|
Если 
, то степенной ряд сходится в единственной точке 
.
На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходиться.
Сходимость степенного ряда при 
и 
исследуется с помощью какого-либо из признаков сходимости.
Пример 1. Найти область сходимости ряда: 
;
Решение. Найдем радиус сходимости данного ряда:
.
Следовательно, данный ряд абсолютно сходится на всей числовой оси.
Пример 2. 
Решение. Воспользуемся признаком Даламбера. Для данного ряда имеем:
, 
,
.
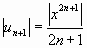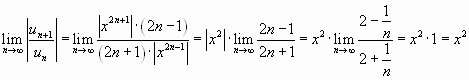Ряд абсолютно сходится, если 
или 
. Исследуем поведение ряда на концах интервала сходимости.
При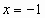 
имеем ряд 
, который сходится по признаку Лейбница.
При 
имеем ряд 
- это тоже сходящийся Лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок 
.
Пример 3. Найти радиус сходимости ряда: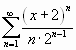 
.
Решение. Найдем радиус сходимости ряда:
.
Следовательно, ряд сходится при 
, т.е. при 
.
При 
имеем ряд 
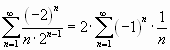, который сходится по признаку Лейбница.
При имеем расходящийся ряд
.
Следовательно, областью сходимости исходного ряда является промежуток 
|
|
|
