 |
Определенный интеграл и его свойства.
|
|
|
|
Определенный интеграл - это число.
Решить определенный интеграл – это значит, найти число. Находим его по формуле Ньютона-Лейбница:
Основные свойства определенного интеграла
1. 
.
2. 
.
3. 
.
4. Если f(x) £ j(x) на отрезке [a, b] a < b, то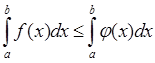 
.
5. Для произвольных чисел a, b, c справедливо равенство: 
, где равенство выполняется, если существует каждый из входящих в него интегралов.
6. 
.
3. Методы интегрирования неопределенного интеграла.
Непосредственный метод интегрирования.
Метод интегрирования основан на применении табличных интегралов, и называется непосредственным интегрированием. При этом данный интеграл может быть приведен к табличному с помощью тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла.
Пр имеры:
a) 
b) 
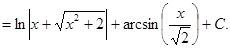
с) 
.
Замена переменной
Интегрирование способом подстановки заслуживает особого внимания, так как этот способ дает возможность привести данный интеграл к табличному. Метод подстановки наиболее широко употребляется, поэтому им надо хорошо владеть.
Пример 1. Найти: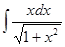 
Решение. Применяя подстановку 
, где t – новое переменное. Возведем обе части равенства в квадрат.
1+x2=t2
Продифференцируем обе части равенства. Получим:
2хdx=2tdt
xdx=tdt
Теперь данный интеграл можно записать: 
Произведя обратную подстановку, получим: 
При интегрировании заменой переменной важно удачно сделать подстановку. Однако нельзя дать общее правило выбора замены переменной для интегрирования любой функции. Это можно сделать только для интегрирования отдельных классов функций: рациональных, тригонометрических и т.д.
|
|
|
Интегрирование по частям
Формула интегрирования по частям: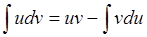 
.
Пример 1. Найти: 
Интегрируется по частям: пусть 
; тогда 
,. 
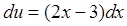Следовательно, 
.
Еще раз интегрируется по частям: пусть 
тогда 
. Получаем,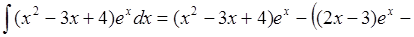 
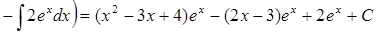
Пример 2. Найти: 
Интегрируется по частям: пусть 
; тогда 
. Следовательно, 
.
Пример 3. Найти: 
Интегрируется по частям: пусть 
; тогда 
, 
. Следовательно, 
.
Получившийся интеграл вычисляется методом замены переменной:
. Тогда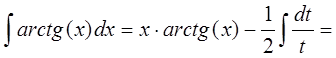 
Пример 4. Найти: 
Пусть 
. Тогда 
.
Интегрируется по частям: пусть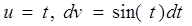 
; тогда 
. Следовательно,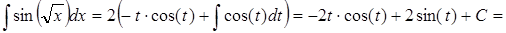 
.
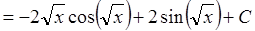Методы интегрирования определенного интеграла.
Непосредственное интегрирование.
Пример1. Найти: 
.
Замена переменных.
Пример2: 1. 
Интегрирование по частям.
Формула имеет вид: 
.
Пример 3: Вычислить: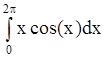 
= 
= 
=
= 
+ 
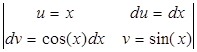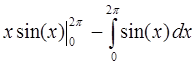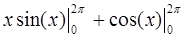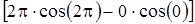=0.
Применение первообразной при вычислении площади фигур.
Вычисление площадей плоских фигур.
Необходимо хорошо усвоить, что с геометрической точки зрения определенный интеграл 
непрерывной функции численно равен площади фигуры, ограниченной кривой y=f(x), осью Ох и прямыми х=а и x=b. Поэтому формулу площади можно записать так:
S= 
Вычисление площадей плоских фигур.
Площадь криволинейной трапеции, ограниченной кривой y = f (x) [ f (x) ≥ 0], прямыми x = a и x = b и отрезками [ a; b ] оси Ох, вычисляется по формуле:
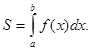(если f(x) выше оси OX)
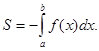(если f(x) ниже оси OX)
Площадь фигуры, ограниченной кривыми y = f 1 (x) и y = f 2 (x) [ f 1 (x) ≤ f 2 (x)] и прямыми x = a и x = b, находится по формуле:
Пример. Вычислить площадь фигуры, ограниченной заданными линиями y =– x 2, y =– x –2.
Решение. Сделаем чертеж.
Найдем абсциссы точек пересечения данных линий:
– x 2=– x –2 или x 2– x –2=0,
x 1=–1, x 2=2.
Значит,
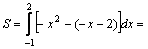
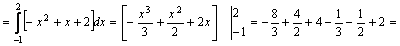–3+1,5+4+2=4,5.
2. Задача о длине пути.
Материальная точка движется с переменной скоростью v(t). Путь, пройденный точкой за промежуток времени T, вычисляется по формуле:
|
|
|
Пример. Скорость прямолинейного движения тела выражается формулой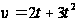 
(м/с). Найти путь, пройденный телом за 5 секунд от начала движения.
◄ Так как путь, пройденный телом со скоростью 
(t) за отрезок времени [t1,t2], выражается интегралом
то имеем: 
►
|
|
|
