 |
Как найти обратную матрицу?
|
|
|
|
Рассмотрим квадратную матрицу  . Обратную матрицу
. Обратную матрицу  можно найти по следующей формуле:
можно найти по следующей формуле:
 , где
, где  – определитель матрицы
– определитель матрицы  ,
,  – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .
.
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Обозначения: Как вы уже, наверное, заметили, обратная матрица обозначается надстрочным индексом 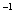
Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.
Пример:
Найти обратную матрицу для матрицы 
Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.

Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось,  , а значит, всё в порядке.
, а значит, всё в порядке.
2) Находим матрицу миноров  .
.
Матрица миноров имеет такие же размеры, как и матрица  , то есть в данном случае
, то есть в данном случае  .
.
Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.
Возвращаемся к нашей матрице 
Сначала рассмотрим левый верхний элемент:

Как найти его минор?
А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:

Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров:

Рассматриваем следующий элемент матрицы  :
:

Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент:

То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу:

Аналогично рассматриваем элементы второй строки и находим их миноры:


Готово.
|
|
|
 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы  .
.
3) Находим матрицу алгебраических дополнений  .
.
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел:

Именно у этих чисел, которые я обвел в кружок!
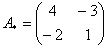 – матрица алгебраических дополнений соответствующих элементов матрицы
– матрица алгебраических дополнений соответствующих элементов матрицы  .
.
И всего-то лишь…
4) Находим транспонированную матрицу алгебраических дополнений  .
.
 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .
.
5) Ответ.
Вспоминаем нашу формулу 
Всё найдено!
Таким образом, обратная матрица:
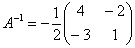
Как проверить решение?
Необходимо выполнить матричное умножение  либо
либо 
Проверка:

Получена уже упомянутая единичная матрица – это матрица с единицами на главной диагонали и нулями в остальных местах.
Таким образом, обратная матрица найдена правильно.
Переходим к более распространенному на практике случаю – матрице «три на три»:
Пример:
Найти обратную матрицу для матрицы 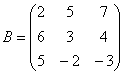
Алгоритм точно такой же, как и для случая «два на два».
Обратную матрицу найдем по формуле:  , где
, где  – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .
.
1) Находим определитель матрицы.
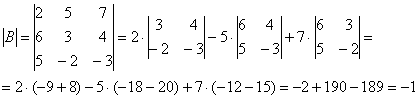
Здесь определитель раскрыт по первой строке.
Также не забываем, что  , а значит, всё нормально – обратная матрица существует.
, а значит, всё нормально – обратная матрица существует.
2) Находим матрицу миноров  .
.
Матрица миноров имеет размерность «три на три»  , и нам нужно найти девять чисел.
, и нам нужно найти девять чисел.
Я подробно рассмотрю парочку миноров:
Рассмотрим следующий элемент матрицы:

МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:

Оставшиеся четыре числа записываем в определитель «два на два»

Этот определитель «два на два» и является минором данного элемента. Его нужно вычислить:
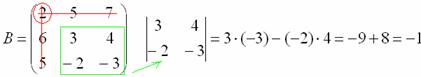
Всё, минор найден, записываем его в нашу матрицу миноров:

|
|
|
Как вы, наверное, догадались, необходимо вычислить девять определителей «два на два». Процесс, конечно, муторный, но случай не самый тяжелый, бывает хуже.
Ну и для закрепления – нахождение еще одного минора в картинках:

Остальные миноры попробуйте вычислить самостоятельно.
Окончательный результат:
 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы  .
.
То, что все миноры получились отрицательными – чистая случайность.
3) Находим матрицу алгебраических дополнений  .
.
В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов:

В данном случае:
 – матрица алгебраических дополнений соответствующих элементов матрицы
– матрица алгебраических дополнений соответствующих элементов матрицы  .
.
4) Находим транспонированную матрицу алгебраических дополнений  .
.
 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .
.
5) Ответ:

Проверка:

Таким образом, обратная матрица найдена правильно.
Пример 1
Умножить матрицы

Решение: произведение существует, причём итоговая матрица состоит из 1 строки и 2 столбцов:

Ответ: 
Пример 3
Возвести в квадрат матрицу 

Ответ: 
Метод Гаусса
Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас я сразу нарисую результат, к которому мы придём в ходе решения:

И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?
Сначала смотрим на левое верхнее число:

Почти всегда здесь должна находиться единица. Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения. Уже легче.
Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2:

|
|
|
Результат записываем во вторую строку:

Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3. Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3:

Результат записываем в третью строку:

На практике эти действия обычно выполняются устно и записываются в один шаг:
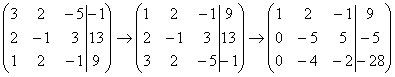
Не нужно считать всё сразу и одновременно. Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО:

А мысленный ход самих расчётов я уже рассмотрел выше.
Далее нужно получить единицу на следующей «ступеньке»:
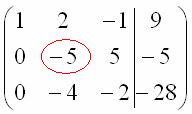
В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2:

Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений:

Круто.
Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
В третьем уравнении у нас уже готовый результат: 
Смотрим на второе уравнение:  . Значение «зет» уже известно, таким образом:
. Значение «зет» уже известно, таким образом:

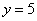
И, наконец, первое уравнение:  . «Игрек» и «зет» известны, дело за малым:
. «Игрек» и «зет» известны, дело за малым:



Ответ: 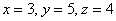
Метод Крамера
|
|
|


