 |
Теорема сложения вероятностей несовместных событий.
|
|
|
|
Суммой конечного числа событий называется событие, состоящее в наступлении хотя бы одного из них.
Сумму двух событий обозначают символом А+В, а сумму n событий символом А1+А2+ … +Аn.
Теорема сложения вероятностей.
Вероятность суммы двух несовместных событий равна 
сумме вероятностей этих событий.
или
Следствие 1. Если событие А1, А2, …,Аn образуют полную систему, то сумма вероятностей этих событий равна единице.
.
Следствие 2. Сумма вероятностей противоположных событий 
и 
равна единице.
.
Пример 1. Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 20000 руб., на 10 - по 15000 руб, на 15 - по 10000 руб., на 25 - по 2000 руб. и на остальные ничего. Найти вероятность того, что на купленный билет будет получен выигрыш не менее 10000 руб.
Решение. Пусть А, В, и С- события, состоящие в том, что на купленный билет падает выигрыш, равный соответственно 20000, 15000 и 10000 руб. так как события А, В и С несовместны, то
.
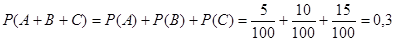Пример 2. На заочное отделение техникума поступают контрольные работы по математике из городов А, В и С. Вероятность поступления контрольной работы из города А равна 0,6, из города В - 0,1. Найти вероятность того, что очередная контрольная работа поступит из города С.
Решение. События «контрольная работа поступила из города А», «контрольная работа поступила из города В» и «контрольная работа поступила из города С» образуют полную систему, поэтому сумма их вероятностей равна единице:
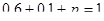, т.е. 
.
Пример 3. Вероятность того, что день будет ясным, 
. Найти вероятность 
того, что день будет облачным.
Решение. События «день ясный» и «день облачный» противоположные, поэтому
, т.е 
.
Теорема умножения вероятностей независимых событий
|
|
|
Теорема умножения вероятностей
Вероятность одновременного появления двух независимых событий равна произведению вероятностей этих событий:
.
Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле
.
Пример 1. В первой урне находится 6 черных и 4 белых шара, во второй- 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми.
Решение. Пусть 
- из первой урны извлечен белый шар; 
- из второй урны извлечен белый шар. Очевидно, что события 
и независимы.
Так как 
, 
, то по формуле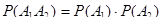 
находим
.
Пример 2. Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента равна 0,2; вероятность выхода из строя второго элемента равна 0,3. Найти вероятность того, что: а) оба элемента выйдут из строя; б) оба элемента будут работать.
Решение. Пусть событие А - выход из строя первого элемента, событие В - выход их строя второго элемента. Эти события независимы (по условию).
а) Одновременное появление А и В есть событие АВ. Следовательно,
.
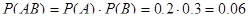б) Если работает первый элемент, то имеет место событие 
(противоположное событию А - выходу этого элемента из строя); если работает второй элемент- событие В. Найдем вероятности событий и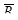 
:
;
.
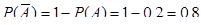Тогда событие, состоящее в том, что будут работать оба элемента, есть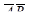 
и, значит,
.
Математическое ожидание и дисперсия случайной величины.
Случайная величина.
Часто в результате испытания происходят события, заключающиеся в том, что некоторая величина принимает одно из своих возможных значений.
В таких случаях удобно вместо множества событий рассматривать одну переменную величину (называемую случайной величиной). Случайная величина обозначается через X, Y, Z, … и т.д.
Случайной называется величина, которая в результате испытания может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.
Пример 1. В студенческой группе 25 человек. Пусть величина Х – число студентов, находящихся в аудитории перед началом занятий. Ее возможными значениями будут числа 0, 1, 2,…,25.
При каждом испытании (начало занятий) величина Х обязательно примет одно из своих возможных значений, т.е. наступит одно из событий Х = 0, Х = 1, …, Х = 25.
Пример 2. Измерение курса акции некоторого предприятия. Возможные события заключаются в том, что стоимость акции Y примет некоторое значение в пределах от 0 до ∞.
Пример 3. Однократное бросание игральной кости. Возможные события заключаются в том, что на верхней грани выпадает Z: 1, 2, 3, 4, 5, 6.
Пример 4. Подбрасывается монета n раз. Возможные результаты: герб выпал 0, 1, 2, …, n раз.
Различают дискретные и непрерывные случайные величины.
Если множество возможных значений случайной величины конечно или образуют бесконечную числовую последовательность, то такая случайная величина называется дискретной.
Случайная величина, множество значений которой заполняет сплошь некоторый числовой промежуток, называется непрерывной. Заметим, что дискретные и непрерывные величины не исчерпывают все типы случайных величин.
Если случайная величина не относится ни к дискретным, ни к непрерывным случайным величинам, то ее называют смешанной.
Очевидно, что для полной характеристики дискретной случайной величины мало знать ее значения. Необходимо им поставить в соответствие вероятности.
Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины.
Простейшая формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины (обычно в порядке возрастания) и соответствующие им вероятности:
|
|
|
| Х | х 1 | х 2 | … | хn | … |
| Р | р 1 | р 2 | … | рn | … |
Такая таблица называется рядом распределения.
Допустим, что число возможных значений случайной величины конечно: х 1, х 2, …, хn. При одном испытании случайная величина принимает одно и только одно постоянное значение. Поэтому события Х = хi (i = 1, 2, …, n) образуют полную группу попарно независимых событий. Следовательно, р 1 + р 2 + … + рn = 1.
Можно закон распределения изобразить и графически, откладывая на оси абсцисс возможные значения случайной величины, а на оси ординат – соответствующие вероятности. Для большей выразительности полученные точки соединяются прямолинейными отрезками. Получающая при этом фигура называется многоугольником (полигоном) распределения.
|
|
|
Закон распределения непрерывной случайной величины удобно задавать с помощью функции плотности вероятности 
.
Вероятность 
того, что значение, принятое случайной величиной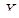 
, попадет в промежуток (а, в), определяется равенством
.
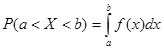График функции называется кривой распределения. Геометрически вероятность попадания случайной величины в промежуток (а, в) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью Ох и прямыми х=а, х=в.
Пример 5. Даны вероятности значений случайной величины 
: значение 10 имеет вероятность 0,3; значение 2 – вероятность 0,4; значение 8 – вероятность 0,1; значение 4 – вероятность 0,2. Построить ряд распределения случайной величины .
Решение. Расположив значения случайной величины в возрастающем порядке, получим ряд распределения:
| 2 | 4 | 8 | 10 |
| 0,4 | 0,2 | 0,1 | 0,3 |
Возьмем на плоскости хОр точки (2; 0,4), (4; 0,2), (8; 0,1) и (10; 0,3). Соединив последовательные точки прямолинейными отрезками, получим многоугольник (или полигон) распределения случайной величины
|
|
|
