 |
Разложение элементарных функций в ряд Тейлора.
|
|
|
|
Если функция  в некотором интервале раскладывается в степенной ряд по степеням
в некотором интервале раскладывается в степенной ряд по степеням  , то это разложение единственно и задается формулой:
, то это разложение единственно и задается формулой:

Пример 4. Разложить функцию  в ряд Тейлора по степеням
в ряд Тейлора по степеням 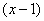
В данном случае 







 , все производные, начиная с четвёртой производной, будут нулевыми.
, все производные, начиная с четвёртой производной, будут нулевыми.
Теперь подставляем в формулу Тейлора:

Пример 5. Разложить функцию  в ряд Тейлора по степеням
в ряд Тейлора по степеням  .
.
Решение: 







А теперь проанализируем найденные производные:
 ,
,  ,
,  .
.
Закономерность прослеживается: знаки чередуются, в числителе накручивается факториал, а в знаменателе растёт степень.
Теперь, исходя из выявленной закономерности, нужно составить производную «энного» порядка. В данном случае она выглядит так:

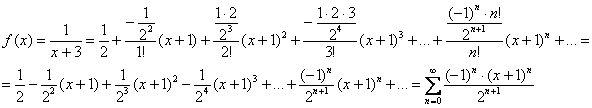
Пример 6. Разложить функцию  в ряд Тейлора по степеням
в ряд Тейлора по степеням  .
.
Решение : Используем разложение функции в ряд Тейлора по степеням  :
:

В данном случае: 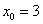







…


…
Таким образом:

Если  , то получим частный случай ряда Тейлора
, то получим частный случай ряда Тейлора
 , который называется
, который называется
рядом Маклорена.
Таблица, содержащая разложения в ряд Маклорена некоторых элементных функций:
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
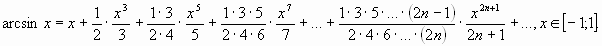
Пример 7. Разложить в ряд Маклорена функцию  .
.
Решение. Так как  , то, заменяя
, то, заменяя  на
на 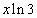 в разложении
в разложении 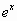 , получим:
, получим:
 ,
,  .
.
Пример 8. Выписать ряд Маклорена функции  .
.
Решение. Так как  , то воспользовавшись формулой
, то воспользовавшись формулой  , в которой заменим
, в которой заменим  на
на  , получим:
, получим:
 ,
,
или
 ,
,
если
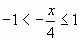 , т.е.
, т.е.  .
.
Пример 9. Разложить в ряд Маклорена функцию  .
.
Решение. Воспользуемся формулой  . Так как
. Так как
 , то заменив
, то заменив  на
на  получим:
получим:
 , или
, или
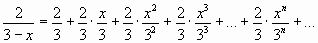 ,
,
где  , т.е.
, т.е.  .
.
Множества и операции над ними.
Определение множества
Множеством называется совокупность некоторых элементов.
Множество – совокупность объектов, объединенных по какому – нибудь признаку.
|
|
|
Элементами множества могут быть числа, фигуры, предметы, понятия и т.п. Множества обозначают большими буквами латинского алфавита: А, В, С, D и т. д., а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки.
Обозначения некоторых числовых множеств:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I - множество иррациональных чисел;
R – множество действительных чисел;
C- множество комплексных чисел.
Множество может быть задано одним из двух способов: перечислением и с помощью определяющего свойства.
Перечислением заданы следующие множества:
А={1,2,3,5,7} — множество чисел
Х={x1,x2,…,xn} — множество некоторых элементов x1,x2,…,xn
N={1,2,…,n} — множество натуральных чисел
Z={0,±1,±2,…,±n} — множество целых чисел
С помощью определяющего свойства заданы следующие множества:
А={x |2  x
x  5; x
5; x  N}-множество чисел
N}-множество чисел
B={x |5  x
x  25; x
25; x  N, x=5n}
N, x=5n}
C={x | 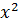 -10x+21=0}
-10x+21=0}
Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит). Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).
1. Виды множеств:
• Равные множества
Два множества А и В равны (А=В), если они состоят из одних и тех же элементов. Если А={1,2,3,4}, B={3,1,4,2} то А=В
• Конечные множества
А = {2; 3; 5; 7; 11; 13};
{х | 5< х <12}
• Бесконечные множества
{1; 4; 9; 16; 25; …}; {10; 20; 30; 40; 50; …};
• Пустые множества
Пустое множество обозначается символом Ø
Если множество не содержит ни одного элемента, то оно называется пустым множеством и записывается Ø.
Операции над множествами
Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
|
|
|
Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
Разностью множеств А и В называется множество АВ, элементы которого принадлежат множеству А, но не принадлежат множеству В.
Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}
Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).
Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}
Прямым произведением множеств 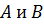 называется множество
называется множество  являющееся?
являющееся?
Например, А=  , В={4;7;9}. Тогда прямое произведение
, В={4;7;9}. Тогда прямое произведение
 ={(6;4);(6;7);(6;9);(8;4);(8;7);(8;9)}
={(6;4);(6;7);(6;9);(8;4);(8;7);(8;9)}
Например, А=  , В={4;7;9}. Тогда прямое произведение
, В={4;7;9}. Тогда прямое произведение
 ={(9;6);(9;8);(7;6);(7;8);(4;6);(4;8)}
={(9;6);(9;8);(7;6);(7;8);(4;6);(4;8)}
Диаграммы Эйлера-Венна.
Для наглядного представления множеств используют диаграммы Эйлера-Венна. В этом случае множества изображают в виде кругов, а основное множество в виде прямоугольника, их содержащего.
1. Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:

На диаграмме объединение множеств А и В выделено штриховкой.
2. Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:

А ∩ В
На диаграмме пересечение множеств А и В выделено штриховкой.
3. Поясним определение разности множеств на диаграмме Эйлера-Венна следующим образом:

На диаграмме разность А\В выделена штриховкой.
Пример 1.
- Множество детей является подмножеством всего населения.
- Пересечением множества целых чисел с множеством поло- жительных чисел является множество натуральных чисел.
- Объединением множества рациональных чисел с множест- вом иррациональных чисел является множество действи- тельных чисел.
Пример 2.
Даны множества А={a;b;c;d;e} и В={c;d;e; f;g}. Тогда А  равно…
равно…
Варианты ответа:
1) {a;b;c;d;e} 2) {c;d;e; f;g} 3) {c;d;e} 4) {a;b;c;d;e; f;g}
Пример 3.
Пусть на рисунке изображены множества А,В,С

Тогда заштрихованная область соответствует множеству…
Варианты ответа:
1) B 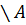 2) A
2) A 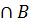 3) A
3) A  4) C
4) C 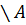
|
|
|
Пример 4.
Даны множества А={x |  -9x+14=0} и B={x |
-9x+14=0} и B={x | 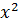 -10x+21=0}
-10x+21=0}
Тогда верными будут утверждения…
Варианты ответа:
1) A 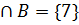 2) A
2) A  3) A
3) A  4) A={2;7}
4) A={2;7}
Пример 5.
Для множества А={2;0; 
 верным будет утверждением…
верным будет утверждением…
Варианты ответа:
1) A  2) A
2) A  3) A
3) A  4) A
4) A 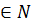
Пример 6.
Пусть А={x | 1  x
x  тогда это множество, заданное перечислением всех его элементов, имеет вид...
тогда это множество, заданное перечислением всех его элементов, имеет вид...
Варианты ответа:
1) А={1;2;3;4;5...}; 2) A={2;3;4}; 3) A={1;2;3;4;5...}; 4) A={1;2;3;4;5}
Пример 7.
Пусть А={a;b;c} B={3;5}. Тогда прямое произведение А  равно...
равно...
Варианты ответа:
1) {(a;3);(a;5);(b;3);(b;5)(c;3);(c;5)}
2) {(5;c);(5;b);(5;a);(3;c);(3;d);(3;a)}
3) {a3;a5;b3;b5;c3;c5}
4){(a;3);(a;5);(b;3);(b;5)}
Пример 8.
Даны множества A={1;2;3;4;5} и B={3;4;5;6;7}. Тогда A 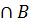 равно...
равно...
Варианты ответа:
1) {1;2;3;4;5;6;7} 2) {3;4;5;6;7} 3) {3;4;5} 4) {1;2;3;4;5}
Пример 9.
Даны множества А={x | x 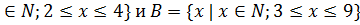 Тогда верным будет утверждения...
Тогда верным будет утверждения...
Варианты ответа: Укажите не менее двух вариантов ответа
1) А  2) В={3;4;5;6;7;8;9} 3) A
2) В={3;4;5;6;7;8;9} 3) A  4) A={3}
4) A={3}
Пример 10. Пусть A есть отрезок [1, 3], B - отрезок [2, 4]; тогда объединением  будет отрезок [1, 4], пересечением
будет отрезок [1, 4], пересечением 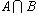 - отрезок [2, 3], разностью A \ B - полуинтервал [1, 2), B \ A - полуинтервал (3, 4].
- отрезок [2, 3], разностью A \ B - полуинтервал [1, 2), B \ A - полуинтервал (3, 4].
Пример 11. В фотоальбоме много фотографий. На 21 фотографии моя сестра. На 30 – я. На 14 – мы с сестрой фотографировались вместе. А на 6 фотографиях нет ни одного человека, там изображена природа. Сколько фотографий в фотоальбоме?
Решение:
Пусть A – множество фотографий с моей сестрой. По условию A={21}.
Пусть B – множество фотографий со мной. Количество элементов B={30}.
Пусть C – множество фотографий меня и сестры. По условию C={14}.
Пусть D – множество фотографий с природой. По условию D={6}.
Пусть K – множество всех фотографий.
A+B-C+D=21+30-14+6=K K= {43}.
Ответ:48 фотографий в фотоальбоме.
Пример 12. На полках стояло 20 дисков, причём на каждом есть запись. Известно, что 14 дисков с мультиками, а 16 с фильмами. На каком диске записаны и мультики, и фильмы?
Решение:
Пусть А – это множество дисков с записью мультиков. Количество элементов в нём, по условию: A={14}
Пусть B – множество дисков с фильмами.
Количество элементов в нём: B={16}
|
|
|
Пусть x – количество дисков с мультиками и фильмами.
A+B-х=14+16-х=20 х= {10}
Ответ: на 10-ти дисках записаны и мультики, и фильмы.
|
|
|


