 |
Выборка. Генеральная совокупность. Медиана. Среднее арифметическое.
|
|
|
|
Всю совокупность объектов, подлежащих изучению, называют генеральной совокупностью. Генеральной совокупностью могут быть всё население страны, месячная продукция завода и т.д.
Та часть объектов, которая попала на проверку, исследование и т.п., называется выборочной совокупностью или просто выборкой.
Число элементов в генеральной совокупности и выборке называется их объёмами.
Различные значения случайной величины называются вариантами.
Вариационным рядом называется ряд, расположенный в порядке возрастания (или убывания) вариантов с соответствующими им частотами.
Вариационный ряд может быть дискретным или непрерывным.
Пример 1. Дана выборка: 1,3; 1,8; 1,2; 3,0; 2,1; 5; 2,4; 1,2; 3,2;1,2; 4; 2,4.
Это ряд вариантов. Расположив эти варианты в возрастающем порядке, мы получим вариационный ряд: 1,2; 1,2; 1,2; 1,3; 1,8; 2,1; 2,4; 2,4; 3,0; 3,2; 4; 5.
Составим таблицу:
| xi | 1,2 | 1,3 | 1,8 | 2,1 | 2,4 | 3,0 | 3,2 | 4 | 5 |
| ni | 3 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 |
| ni/n | 3/12=1/4 | 1/12 | 1/12 | 1/12 | 2/12 | 1/12 | 1/12 | 1/12 | 1/12 |
Такие таблицы называют частотными. В них числа второй строки – частоты; они показывают, как часто встречаются в выборке те или другие её значения.
Относительной частотой значений выборки называют отношение её частоты к числу всех значений выборки.(значения в третьей строке таблицы)
Выборки характеризуются центральными тенденциями: средним значением, модой и медианой.
Средним значением выборки называют среднее арифметическое всех её значений.
Модой вариационного ряда называют вариант (значение случайной величины), которому соответствует наибольшая частота (Мо), т.е. которая встречается чаще других.
Медиана выборки – это число, “разделяющее” пополам упорядоченную совокупность всех значений выборки или Медианой вариационного ряда называется то значение случайной величины, которое приходится на средину вариационного ряда (Ме).Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.
|
|
|
Размахом ряда называется разность между R=xmax - xmin, т.е. наибольшим и наименьшим значениями этих вариантов.
Пример 2. Дана выборка: 1,3; 1,8; 1,2; 3,0; 2,1; 5; 2,4; 1,2; 3,2;1,2; 4; 2,4.
Это ряд вариантов. Расположив эти варианты в возрастающем порядке, мы получим вариационный ряд: 1,2; 1,2; 1,2; 1,3; 1,8; 2,1; 2,4; 2,4; 3,0; 3,2; 4; 5.
Сосчитали число членов, их 12 - чётное число членов, значит надо найти среднее арифметическое двух чисел записанных посередине, то есть 6 и 7-ой варианты. (2,1+2,4)\2=2.25 – медиана.
Модой является 1.2, т.к. только это число встречается 3 раза, а остальные встречаются меньше, чем 3 раза.
Среднеарифметическое значение находим так:
(1,2*3+1,3+1,8+2,1+2,4*2+3,0+3,2 +4+5)\12=2,4
Среднее значение этого ряда равно 2,4.
Медиана ряда 2,25.
Мода ряда –1,2.
Размах ряда: R=5-1,2=3,8.
Численное интегрирование.
Одномерный определенный интеграл вида:
 (1)
(1)
с пределами интегрирования  можно трактовать как площадь фигуры, ограниченной отрезками прямых
можно трактовать как площадь фигуры, ограниченной отрезками прямых  , осью абсцисс и графиком подынтегральной функции
, осью абсцисс и графиком подынтегральной функции  Если известна первообразная
Если известна первообразная  для
для  то интеграл легко определяется по формуле Ньютона-Лейбница
то интеграл легко определяется по формуле Ньютона-Лейбница  Для некоторых подынтегральных функций
Для некоторых подынтегральных функций 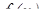 интеграл можно вычислить аналитически, найти в справочниках или оценить с помощью асимптотических рядов. Однако в общем случае
интеграл можно вычислить аналитически, найти в справочниках или оценить с помощью асимптотических рядов. Однако в общем случае  может быть не определена: либо первообразные не выражаются через элементарные функции, либо сами
может быть не определена: либо первообразные не выражаются через элементарные функции, либо сами
|
|
|
 Рис. 1
Рис. 1
подынтегральные функции не являются элементарными. Это приводит к необходимости разработки приближенных методов вычисления определенных интегралов.
Наиболее общеупотребительными приближенными методами вычисления одномерных определенных интегралов являются так называемые классические» методы численного интегрирования по квадратурным формулам: метод прямоугольников, метод трапеций, метод парабол (основанные на суммировании элементарных площадей, на которые разбивается вся площадь под функцией  .
.
Во всех этих методах отрезок интегрирования  разбивается на достаточно большое число равных частей, на которых строятся искомые площади (рис. 2):
разбивается на достаточно большое число равных частей, на которых строятся искомые площади (рис. 2):
 и
и 
Оценкой площади под кривой  служит сумма площадей криволинейных трапеций
служит сумма площадей криволинейных трапеций  Простой прием построения формул для расчета интегралов состоит в том, что подынтегральная функция
Простой прием построения формул для расчета интегралов состоит в том, что подынтегральная функция  заменяется
заменяется
на отрезке  интерполяционным многочленом
интерполяционным многочленом  и получается приближенное равенство
и получается приближенное равенство


Рис.2
Метод прямоугольников
Простейшей оценкой искомой площади служит сумма площадей прямоугольников, заменяющих криволинейные трапеции, как показано на рисунке 3.а.

Рис.3
В обычном методе прямоугольников значение  вычисляется в начале каждого отрезка и оценка интеграла дается выражением
вычисляется в начале каждого отрезка и оценка интеграла дается выражением
 где
где 
Просуммировав элементарные площади фигур, построенных на сегментах  получим примерное значение искомого определенного интеграла
получим примерное значение искомого определенного интеграла
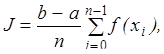 где
где  (2.а)
(2.а)
Одна из модификаций метода прямоугольников заключается в вычислении  не в начальной, а в средней точке каждого отрезка (рис.8.3.б). В этом случае искомый интеграл оценивается выражением
не в начальной, а в средней точке каждого отрезка (рис.8.3.б). В этом случае искомый интеграл оценивается выражением
 где
где  (2.б)
(2.б)
Метод трапеций
Другим приближением является формула трапеций, в которой интеграл оценивается вычислением суммы площадей элементарных трапеций со сторонами, равными значениям  в начале и конце элементарного отрезка. Это приближение равносильно замене функции отрезком прямой, соединяющей значения
в начале и конце элементарного отрезка. Это приближение равносильно замене функции отрезком прямой, соединяющей значения  в начальной и конечной точках отрезка (рис.4).
в начальной и конечной точках отрезка (рис.4).
 Рис.4
Рис.4
|
|
|
Площадь каждого элементарного сегмента разбиения считается по формуле
 где
где 
Полная площадь определяется выражением
 (3)
(3)
Формула прямоугольников

Формула трапеций

Формула парабол (метод Симпсона)
 ƒ
ƒ 
Пример 1. Вычислить по формуле прямоугольников определенный интеграл  .
.
Решение:
Положим n = 10, т.е. разбиваем интервал интегрирования от 1 до 2 на десять равных частей.

Вычислим значение функции в точках разбиения:
x0=1 
x1=1,1 
x2=1,2 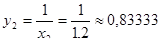
x3=1,3 
x4=1,4 
x5=1,5 
x6=1,6 
x7=1,7 
x8=1,8 
x9=1,9 
Сумма 7,18773
По формуле получаем:  .
.
Полученное значение больше истинного, т.к. кривая  обращена к оси х своей выпуклостью.
обращена к оси х своей выпуклостью.
Вычислим остаточный член по формуле. Для этого предварительно определяем первую производную подынтегральной функции: 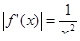
представляет собой убывающую функцию и следовательно максимальное значение принимает при меньшем х из заданного интервала  , т.е. при х =1:
, т.е. при х =1:
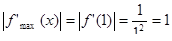
Подставляя в формулу, окончательно получаем:

Ошибка округления существенно меньше полученного R и, следовательно, ее можно не учитывать.
Окончательно получаем:
 .
.
Пример 2. Вычислить по формуле трапеций определенный интеграл  . Оценить погрешность вычислений.
. Оценить погрешность вычислений.
Решение:
Положим n=10. Воспользуемся вычисленными в задании 1 значениями функции в точках разбиения. По формуле

найдем значение определенного интеграла:
 +0,90909+0,83333+0,76923+0,71429+0,66667+
+0,90909+0,83333+0,76923+0,71429+0,66667+
+0,625+0,55556+0,58824+0,52632+  .
.
3. Вычислить по формуле Симпсона интеграл 

|
|
|


