 |
Примеры решения типовых задач. DHисп = lисп×МHg = 283,2 Дж/г ×200,6 г/моль =
|
|
|
|
1. Температура кипения ртути при нормальном атмосферном давлении равна 357°С. Теплота испарения равна 283,2 Дж/г. Определить изменение давления пара ртути при изменении температуры на 1°С вблизи температуры кипения ртути при нормальном атмосферном давлении.
Решение:

Т = 357 + 273 = 630 К
D H исп = l исп× М Hg = 283,2 Дж/г ×200,6 г/моль =
= 56810 Дж/моль

2. Давление паров воды при 97°С равно 90919,9 Па, а при 103°С – 112651,8 Па. Определить давление паров воды при 110°С.
Решение:






р 3 = 143,4 кПа.
3. Удельная теплота плавления нафталина при t пл = 79,9оС равна 149,25 Дж/г. Разность удельных объемов в жидком и твердом состояниях (D V) при 79,9°С равна 0,146 см3/г. Определить изменение Т пл нафталина при увеличении давления в 100 раз по сравнению с атмосферным.
Решение:
 ;
; 
Т пл = 79,9 + 273 = 352,9 К
Так как давление дано в Па, а D H пл в Дж/г то D V должно быть выражено в м3/кг, а энтальпия плавления в Дж/кг.
 3,452×10–7 К/Па
3,452×10–7 К/Па
D Т пл = 3,452×10–7×(101,3×102×103 – 101,3×103) = 3,46 К.
Задачи для самостоятельного решения
1. Энтальпия испарения воды при температуре кипения при нормальном атмосферном давлении равна 2258,4 Дж/г. Определить изменение давления пара воды при изменении температуры на 1°С вблизи температуры кипения.
(Ответ: 3561 Па/К)
2. Температура кипения ртути при нормальном атмосферном давлении равна 357°С. Изменение давления пара ртути при изменении температуры на 1°С вблизи температуры кипения при нормальном атмосферном давлении равно 1,744×103 Па. Вычислить энтальпию испарения ртути в Дж/г.
(Ответ: 283 Дж/г)
3. Давление паров воды при 95° и 97°С соответственно равно 84513 и 90920 Па. Вычислить энтальпию испарения воды (Дж/моль) и количество теплоты, необходимое для испарения 100 кг воды.
|
|
|
(Ответ: 41,36 кДж/моль; 229,8 МДж)
4. Давление паров иода при 90°С равно 3572,4 Па, а при 100°С – 6065,15 Па. Определить давление паров иода при температуре 115оС.
(Ответ: 12748 Па)
5. Температура плавления (°С) нафталина в зависимости от давления (Па) выражается уравнением

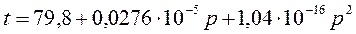
Разность удельных объемов в жидком и твердом состоянии равна 0,146×10–3 м3/кг. Рассчитать энтальпию плавления при давлении 50,66×105 Па.
(Ответ: 187,4 кДж/кг)
6. Зависимость давления p пара никотина C10H14N2 от температуры t имеет вид (1 атм =760 мм рт. ст.)
| t, °С | |||||||
| p, мм рт. ст. |
По графику зависимости ln p от 1/ T рассчитайте энтальпию испарения в указанном интервале температур.
(Ответ: 41,29 Дж/моль)
Фазовые равновесия в двухкомпонентных системах, перегонка
Основные уравнения
Если система состоит из двух компонентов, а на состояние равновесия влияют такие внешние факторы, как температура и давление, то правило фаз Гиббса имеет вид:
| С = 2 – Ф + 2 = 4 – Ф. | (145) |
При Сmin = 0 число фаз Ф = 4. Следовательно, в двухкомпонентной системе число фаз, одновременно находящихся в равновесии, не может быть больше четырех (ж, п, Ат, Вт). Максимальное число степеней свободы Сmax при Фmin = 1 равно 3 (давление, температура и концентрации х 1 одного из компонентов). При выражении концентрации в процентах или долях x 1 = 1 – х 2 и при выбранных параметрах (р, Т, х 1 = 1 – х 2) состояние двухкомпонентной системы можно изобразить с помощью трехмерной диаграммы. Часто состояние двухкомпонентных систем изучают при p = const или T = const. В этом случае уравнение (145) приобретает вид
| С = 2 – Ф + 1 = 3 – Ф, | (146) |
а диаграмма, построенная в координатах "температура – состав" или "давление – состав", будет плоской.
Равновесие «твердое вещество – жидкость».
Фазовая диаграмма системы с простой эвтектикой
Равновесия в системах «твердое вещество – жидкость» встречаются при изучении различных металлических сплавов, силикатов, водных растворов солей, систем, состоящих из органических соединений.
|
|
|
Особое значение имеют исследования зависимостей температур начала и конца кристаллизации твердых веществ от состава системы. Графики, выражающие эту зависимость, называются фазовыми диаграммами или диаграммами плавкости.
Диаграммы плавкости строятся на основании результатов термического анализа, который заключается в наблюдении за скоростью охлаждения расплавленных чистых веществ и их смесей.
Диаграммы такого типа отвечают бинарным системам, в которых вещества неограниченно смешиваются в жидком состоянии, образуя гомогенный раствор и практически не растворяются в твердом состоянии, образуя гетерогенную систему из твердых фаз.
Рассмотрим построение и анализ такой диаграммы на примере системы из веществ А и В.
|

Рис. 41. Фазовая диаграмма системы
с простой эвтектикой
Линия  – линия ликвидуса, линия MN – линия солидуса, они разбивают диаграмму на четыре области:
– линия ликвидуса, линия MN – линия солидуса, они разбивают диаграмму на четыре области:
· область I –жидкий расплав;
· область II – гетерогенная система, состоящая из кристаллов вещества А и жидкого расплава переменного состава;
· область III – гетерогенная система, состоящая из кристаллов вещества В и жидкого расплава переменного состава;
· область IV – гетерогенная система, состоящая из смеси кристаллов А и В.
Каждая точка на диаграмме называется фигуративной и соответствует одному строго определенному состоянию системы в зависимости от того, где эта точка лежит.
Чтобы найти состав сосуществующих фаз, надо через фигуративную точку провести горизонталь до пересечения с граничными линиями, из точки пересечения с одной граничной линией опустить перпендикуляр на ось состава – это даст состав одной фазы, из другой – состав другой фазы. Например, для того чтобы найти состав сосуществующих фаз в точке r, проведем горизонталь до пересечения с линией ликвидус и опустим перпендикуляр из точки пересечения (S), определим массовую долю В в расплаве (ωВ), второй конец горизонтали пересекается с левой осью ординат, соответствующей чистому веществу А, находящемуся при температуре tr, ниже температуры его плавления (t0А), следовательно вещество А находится в виде кристаллов.
|
|
|
Диаграмма плавкости позволяет определить не только число фаз и их состав, но и относительные массы фаз, с помощью правила рычага:
 , ,
| (147) |
где g ж – масса расплава, г; g тв – масса кристаллов, г.
Отрезки trr и rS измеряются на диаграмме в сантиметрах или миллиметрах (рис. 41).
Одним из методов построения диаграмм состояния является метод термического анализа, который заключается в построении кривых охлаждения. Рассмотрим пример: расплавим чистое вещество А и будем его равномерно охлаждать, измеряя температуру. Нанеся эти данные на график, получим кривую охлаждения (рис. 42). Кривая охлаждения любого чистого вещества (однокомпонентная система K = 1) будет состоять из трех участков ab, bc, cd.

Рис. 42. Кривая охлаждения чистого вещества
Изломы на кривых охлаждения (графиках в координатах «температура – время») свидетельствуют об изменении числа фаз в системе (рис. 42 и 43).
Участок ab соответствует охлаждению чистого жидкого вещества А, так как охлаждение ведется равномерно, то он соответствует прямой линии, наклоненной под определенным углом. Число степеней свободы (С) в такой системе рассчитываем по правилу фаз Гиббса: С = K – Ф + n; n = 1, а С = 1 – 1 + 1 = 1 (то есть температура понижается, но при этом сохраняется жидкая фаза).
Когда в жидкости появятся первые кристаллы, система станет двухфазной (твердая и жидкая фазы), а число степеней свободы становится равным нулю: С = 1 – 2 + 1 = 0. Следовательно, при охлаждении однокомпонентной системы (чистого вещества) температура не может изменяться, на кривой охлаждения появляется горизонтальный участок – участок bc.
Охлаждение системы компенсируется теплотой, которая выделяется при кристаллизации. Таким образом, температура горизонтального участка – это температура кристаллизации чистого вещества А.
Когда вся жидкость закристаллизуется, в системе останется одна фаза – твердая, число степеней свободы снова станет равно 1: С = 1 – 1 + 1 = 1.
Такая же кривая охлаждения соответствует и чистому веществу В, только горизонтальный участок будет наблюдаться при другой температуре (при температуре плавления В).
|
|
|
Теперь к твердому веществу А добавим 10% вещества В, смесь расплавим, получим расплав и будем его охлаждать. По результатам охлаждения построим кривую охлаждения (рис. 43), она состоит из четырех участков: mn, nf, fk и kl.

Рис. 43. Кривая охлаждения смеси
Участок mn соответствует охлаждению расплава:
С = 2 – 1 + 1 = 2.
Как только в расплаве появятся кристаллы вещества А (С = 2 – 2 + 1 = 1), температура системы будет понижаться уже медленнее из-за того, что при образовании кристаллов выделяется теплота, замедляющая охлаждение, на кривой появится изгиб (точка n), который будет указывать температуру начала кристаллизации (Tn). В соответствии с законом Рауля наблюдается понижение температуры замерзания раствора (температура начала выпадения кристаллов) по сравнению с температурой замерзания чистого жидкого вещества, поэтому Tn < TА. Следовательно, участок nf относится к охлаждению системы, состоящей из расплава и кристаллов вещества А.
При температуре Tk в системе появляются и кристаллы вещества В. Так как в твердом состоянии вещества A и В совершенно не растворяются друг в друге, а выделяются в виде самостоятельных твердых фаз, то Ф = 3 (две твердые фазы и жидкая). С = 2 – 3 + 1 = 0.
Температура остается постоянной, на кривой охлаждения наблюдается горизонтальный участок fk, температура, которая ему соответствует (Tk) – это температура конца кристаллизации 10% расплава вещества В.
После окончания кристаллизации (жидкая фаза исчезает), Ф = 2 (кристаллы А и кристаллы В), наблюдается охлаждение гетерогенной твердой системы (участок kl): С = 2 – 2 + 1 = 1.
Вид кривых охлаждения для расплавов других концентраций такой же, только перегиб появляется при строго определенной температуре (т.е. температура начала кристаллизации Tn для расплава индивидуальна). Но конец кристаллизации (горизонтальный участок) для расплавов всех концентраций отвечает одной и той же температуре Tk, ее называют температурой эвтектики.
Таким образом, каждая кривая охлаждения дает возможность определить две температуры –начала и конца кристаллизации.
Если нанести эти температуры на график в координатах «T – состав» и соединить между собой все точки начала кристаллизации (линия ликвидуса) и все точки конца кристаллизации (линия солидуса), то получим диаграмму плавкости, общий вид которой представлен на рисунке 41.
|
|
|


