 |
Примеры решения типовых задач.
|
|
|
|
1. Считая теплоемкость газообразного азота Сp равной 7/2 R, вычислите изменение энтропии 5 г N2 при нагревании от 0 до 120°С при постоянном давлении.
Решение:
2. 500 см3 водорода находится в цилиндре с поршнем, площадь которого равна 5 см2. Давление водорода равно 2 атм. Рассчитать изменение энтропии газа при выдвижении поршня на 100 см (Т – const).
Решение:
Пусть Н2 ведет себя как идеальный газ.
3. Рассчитать изменение энтропии при испарении 1 кг воды при температуре 100°С. Удельная теплота испарения воды равна 2255,15 кДж/кг.
Решение:
4. Рассчитать, пользуясь таблицами термодинамических величин, изменение энтропии в химической реакции
2С(графит) + 3Н2(г) ® С2Н6(г)
в стандартных условиях.
Решение:
S 
(С, графит) = 5,74 Дж/(моль×К);
S (Н2, г) = 130,52 Дж/(моль×К);
S (С2Н6, г) = 229,49 Дж/(моль×К)
D S = S (С6Н6, г) – 2× S (С, графит) – 3× S (Н2, г) =
= 229,49 – 2×5,74 – 3×130,52 = – 173,55 Дж/К.
5. Рассчитать, пользуясь таблицами термодинамических величин, изменение энтропии системы, в которой при температуре 700 К протекает реакция (все вещества газообразные)
2С4Н8 + Н2 ® С8Н18
(бутен-1)
Решение:
S (С4Н8, г) = 305,6 Дж/(моль×К);
S (Н2, г) = 130,52 Дж/(моль×К);
S (С8Н18, г) = 466,73 Дж/(моль×К).
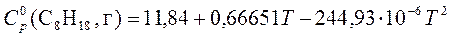
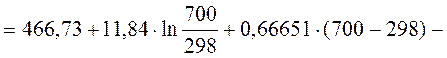
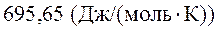
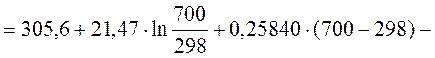
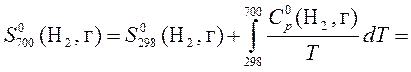
Задачи для самостоятельного решения
1. Рассчитайте, пользуясь таблицами термодинамических величин, изменение энтропии при нагревании 5 моль водяного пара от 110°С до 170°С.
(Ответ: 24,46 Дж/К)
2. Определить изменение энтропии 1 моля идеального газа при изотермическом уменьшении его объема в 10 раз.
(Ответ: –19,14 Дж/К)
3. Найти изменение энтропии при испарении 2 моль жидкого С2Н5Cl (температура кипения равна 12,3°С), если энтальпия испарения равна 3762 Дж/г.
|
|
|
(Ответ: 1701 Дж/К)
4. Найти изменение энтропии в реакции
NO2 = NO + 1/2O2
при температуре 25°С (все вещества находятся в газообразном состоянии).
(Ответ: 73,1 Дж/К)
5. Рассчитать, пользуясь таблицами термодинамических величин, D S ° для реакции
2SO2 + O2 = 2SO3
при температуре 600 К (все вещества находятся в газообразном состоянии).
(Ответ: –176 Дж/К)
Термодинамические потенциалы. Функции Гиббса, Гельмгольца
Основные уравнения
Энергия ГельмгольцаF и энергия ГиббсаG связаны с внутренней энергией и энтальпией, а также друг с другом уравнениями:
| F = U – TS, | (74) |
| G = H – TS, | (75) |
| G = F + pV. | (76) |
а их изменения в процессах, например, в химических реакциях уравнениями:
| D F = D U – D(TS), | (77) |
| D G = D H – D(TS), | (78) |
| D G = D F+ D(pV). | (79) |
Если процесс протекает при постоянной температуре, то уравнения (77) и (78) упрощаются:
| D F = D U – T D S, | (80) | |
| D G = D H – T D S. | (81) | |
Если процесс протекает при постоянном давлении, то уравнение (79) превращается в:
| D G = D F + p D V. | (82) |
Если в физико-химическом процессе (химической реакции) изменяется число молей газообразных веществ и если принять, что газы ведут себя как идеальные газы, то уравнение (82) упрощается:
| D G = D F+ D n×RT. | (83) |
Полный дифференциал функции Гельмгольца имеет вид:
| dF = – pdV – SdT. | (84) |
Уравнения зависимостей функции Гельмгольца от объема (при постоянной температуре) и от температуры (при постоянном объеме) в дифференциальной форме имеют вид:
 ,
| (85) |
 .
| (86) |
а для изменения в каком-либо процессе –
 .
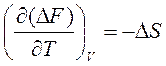| (87) |
В интегральной форме эти уравнения имеют вид:
 ,
| (88) |
 ,
| (89) |
 .
| (90) |
Полный дифференциал функции Гиббса имеет вид:
 .
| (91) |
Уравнения зависимостей функции Гиббса от давления (при постоянной температуре) и от температуры (при постоянном давлении) в дифференциальной форме имеют вид:
 ,
| (92) |
 .
| (93) |
а для изменения в процессе –
 ,
| (94) |
 .
| (95) |
В интегральной форме эти уравнения имеют вид:
|
|
|
 ,
| (96) |
 ,
| (97) |
 ,
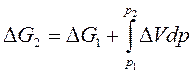| (98) |
 .
| (99) |
Для изотермического процесса расширения 1 моль идеального газа уравнения (88) и (96) упрощаются:
 ,
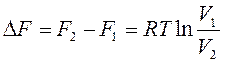| (100) |
 .
| (101) |
Если в процессе участвуют только жидкие или (и) твердые фазы (конденсированные фазы), то уравнение (96) упрощается:
 .
| (102) |
Для процессов фазовых переходов (плавление, кристаллизация, испарение, конденсация и возгонка), которые протекают при постоянном давлении и температуре, из уравнения (91) следует, что:
 .
| (103) |
из уравнения (83) для испарения и возгонки 1 моль вещества, следует что:
| D F исп., возг. = – RT. | (104) |
а для плавления 1 моль вещества из уравнения (84), что:
| D F пл. = 0. | (105) |
Изменение функции Гельмгольца и Гиббса в химической реакции при любой температуре рассчитывается по уравнениям:
 ,
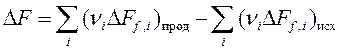| (106) |
 ,
| (107) |
 ,
| (108) |
 .
| (109) |
Изменение функции Гельмгольца и Гиббса (в том числе стандартные) в химической реакции при любой температуре можно рассчитать и по уравнениям (80) и (81), если известны изменения энтальпии и энтропии в реакции:
| D F = D U – T D S, | (110) |
| D G = D H – T D S, | (111) |
| D F 0 = D U 0 – T D S 0, | (112) |
| D G 0 = D H 0 – T D S 0. | (113) |
В изохорно-изотермических (V – const и T – const) условиях процесс протекает самопроизвольно, если:
| dF < 0. | (114) |
В изобарно-изотермических (p – const и T – const) условиях процесс протекает самопроизвольно, если:
| dG < 0. | (115) |
Для тех же условий состояние равновесия достигается, если:
| dF = 0, | (116) |
| dG = 0. | (117) |
|
|
|
