 |
Примеры решения типовых задач. DF = 1 моль×8,314 Дж/К×моль×293 К×lg2 = 1689 Дж
|
|
|
|
1. Рассчитать изменение функции Гельмгольца и Гиббса при изотермическом сжатии в 2 раза 1 моль идеального газа при температуре 20°С.
Решение:
Используя уравнения (100) и (101) получим:
D F = 1 моль×8,314 Дж/К×моль×293 К×lg2 = 1689 Дж
D G = D F = 1689 Дж.
2. Рассчитать D F при испарении 0,5 моль воды при температуре 100°C и давлении 1,0133×105 Па.
Решение:
D F исп. = – nRT = – 0,5 моль×8,314 Дж/(моль×К)×373 К =
= – 1551 Дж.
3. Определите с помощью таблиц термодинамических величин направление самопроизвольного протекания реакции
2С2Н5ОН = С4Н6 + 2Н2О + H2
(бутадиен-1,3)
в стандартных условиях (все вещества находятся в газообразном состоянии).
Решение:
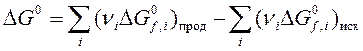
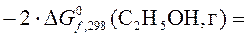
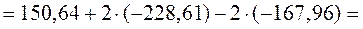29,34 кДж.
Так как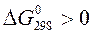 
, то данная реакция в прямом направлении самопроизвольно не протекает.
4. Рассчитать с помощью таблиц термодинамических величин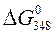 
в реакции
Н2 + Cl2 = 2HСl
(все вещества газообразные) при температуре 348 К, принимая, что изменение энтропии в ходе этой реакции не зависит от температуры.
Решение:
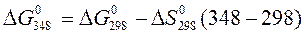
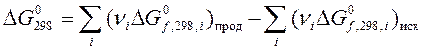
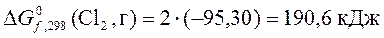
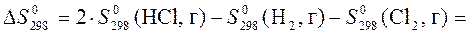
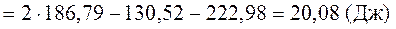
Задачи для самостоятельного решения
1. Рассчитать, пользуясь таблицами термодинамических величин, D F и D G при изотермическом расширении 2 моль идеального газа в 3 раза при температуре 100°С.
(Ответ: – 6813,9 Дж; – 6813,9 Дж)
2. Определить, пользуясь таблицами термодинамических величин, направление самопроизвольного протекания реакции
N2(г) + O2(г) ® 2NO(г)
в стандартных условиях.
(Ответ: D G = 175,16 кДж; справа налево)
3. Рассчитать D G при конденсации 1 кмоль пара воды при температуре 373 К и давлении 1,0133×105 Па.
(Ответ: D G = 0)
4. При обратимом изотермическом сжатии некоторого количества газа в идеальном состоянии от давления р 1 до р 2 D G = 200 Дж. Каково по сравнению с этой величиной будет D G при подобном, но необратимом переходе от р 1 до р 2?
|
|
|
(Ответ: 200 Дж)
ТЕРМОДИНАМИКА ХИМИЧЕСКОГО РАВНОВЕСИЯ
Уравнения химической термодинамики (изотермы химической реакции Вант-Гоффа) позволяют с помощью расчетов по таблицам справочных величин (в том случае, если в них содержится информация о реагентах и продуктах) ответить на вопрос можно ли синтезировать, используя ту или иную химическую реакцию лекарственное вещество. Если реакция возможна, то эти уравнения позволяют рассчитать равновесные концентрации лекарственных веществ и, следовательно, их выход в реакции.
Уравнения изобары и изохоры химической реакции Вант-Гоффа позволяют предсказать влияние изменения температуры на константу равновесия химической реакции, используемой для синтеза лекарственного вещества, и далее рассчитать зависимость выхода вещества от температуры.
1.2.1. Изотерма химической реакции. Расчет констант равновесия химических реакций по термодинамическим таблицам
Основные уравнения
Константа (концентрационная) равновесия химической реакции
v AA + v BВ v CC + v DD
равна:
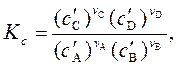
| (118) |
где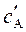 
, 
, 
, 
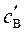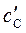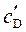– равновесные концентрации участников реакции.
Константа химического равновесия, выраженная через равновесные парциальные давления (
), имеет вид:
 .
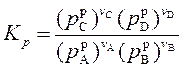| (119) |
Константы равновесия зависят от природы реагирующих веществ, температуры и не зависят от концентрации (Kс) и давления (
). Константы равновесия Kс и безразмерны только для реакций, идущих без изменения числа молей газообразных участников. В остальных случаях имеет размерность давления, а Kс – размерность концентрации в степенях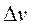 
:
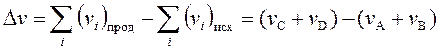
[ Kр ] = [давление]D v и [ Kс ] = [молярная концентрация]D v, где D v – алгебраическая сумма стехиометрических коэффициентов. Константы Kр и Kс связаны соотношением:
| Kр = Kc (RT)D v | (120) |
В случае гетерогенных реакций в выражение константы химического равновесия входят парциальные давления (или концентрации) только газообразных участников реакции. Например, для реакции
|
|
|
СаСO3(т) СаО(т) + СO2(г)
константа равновесия равна
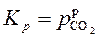
Уравнение изотермы химической реакции
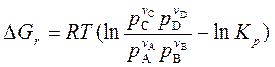
| (121) |
или
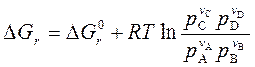
| (122) |
где
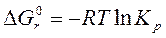
| (123) |
позволяет связать возможное направление реакции с исходным составом реагирующих веществ.
Изменение функции Гиббса реакции в стандартных условиях (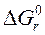
) для реакций, протекающих при 298 К, рассчитывается по формулам:
 .
| (124) |
или
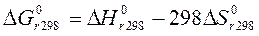
| (125) |
Расчет константы химического равновесия при стандартных условиях и температуре 298 К проводят по уравнению (123), используя значение энергии Гиббса в стандартных условиях:
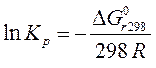
| (126) |
|
|
|
